Mathématiques,
physique appliquées.
Concours interne ingénieur territorial 2017 .
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Problème 1.
La toiture d'une salle polyvalente a pour section transversale une
arche de parabole dont l'axe vertical passe par le centre de la salle.
Les points d'enncrage au sol A et B de cette arche sont distants de 40
m. Le sommet S de celle-ci est situé à 20 m au dessus du sol.
On se propose de partager la salle en deux parties par un rideau de
toile verte, vertical MNPQ touchant le sol et suspendu à une poutre
horizontale MN. La longueur de cette poutre doit être comprise enntre
20 m et 30 m.
On cherche la longueur de poutre permettant d'une part de mettre place
le rideau le moins cher ( donc nécessitant le moins de toile possible)
et d'autre part réalisant la meilleur obturation.
 1.a.
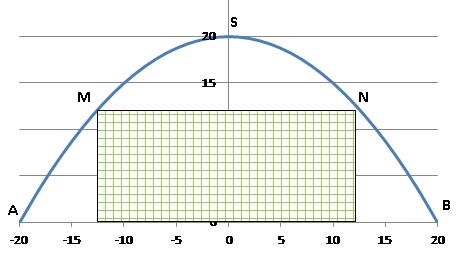
1.a. Dans le repère
( O, i, j ) on considère la parabole (P) ayant pour sommet S(0 ; 20 )
et passant par les points A( -20 ; 0) et B(20 ; 0). Montrer que (P) a
pour équation y = -x 2 / 20 +20. On appelle ( F) l'arc de parabole
correspondant à y >0.
(P) a une équation de la forme y = ax 2 +bx +c avec a, b, c
des constantes.
y' = 2ax +b ; abscisse du sommet x S = -b / (2a) = 0, par
suite b = 0.
(P) passe en A : 0 = 20 2a +c soit c = -400a et y = ax 2-400a
= a(x 2-400).
Ordonnée du sommet : y S = 20 = -400 a ; a = -1 /20 et c = 20.
1.b. x étant un élément de [10 ;
15], on considère les points M et N de (F) d'abscisses respectives
-x et +x ; P et Q sont les projetés orthogonaux sur l'axe des abscisses
de N et M respectivement.
Démontrer que l'aire du rectangle MNPQ est égale à -x3
/10 +40x.
Aire du rectangle MNPQ : PQ * yM = 2x(-x2/20 +20)
= -x3 /10 +40x.
2. Soit la fonction
f définie sur [10 ; 15] par f(x) = -x3 / 10 +40 x.
2.a. Etudier les
variations de f. Quelle est la valeur maximale de f(x) ? Quelle est la
valeur de x correspondante ? Donner les résultats à 10-2
près par défaut.
f '(x) = -3x2 / 10 +40.
f '(x) = 0 pour x = ±20 / 3½ ~ ±11,54.
2.b. Représenter
graphiquement f.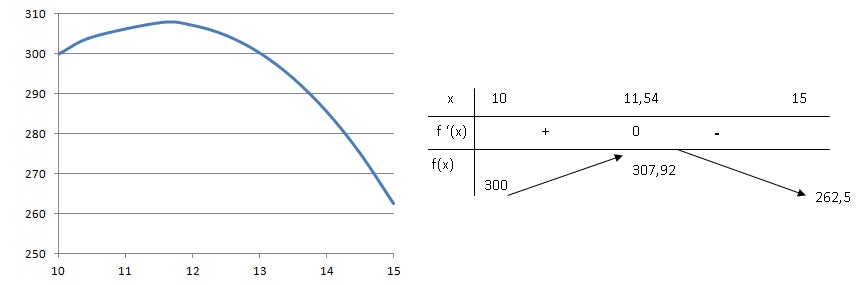
3.a.
En déduire la longueur de la poutre MN permettant de mettre en place le
rideau le plus économique . Quelle est la quantité de toile nécessaire ?
x = 15 ; MN = 30 m ; surface de toile 262,50 m2.
3.b. En
déduire la longueur de MN pouvant supporter le rideau le plus
efficace en matière d'obturation. Quelle est alors la quantité de
toile correspondante ?
x = 11,527 ~11,54 m ; MN = 23,09 m ; surface de toile : 307,92 m2.
|
| .
. |
....
.....
|
Problème
2.
On
considère l'espace vectoriel R3 muni de sa base canonique B
= (i, j, k).
Soit f l'endomorphisme de R3 dont la matrice dans la base B
est M. On note I la matrice unité.
1. Soit l un nombre réel. Montrer
que le déterminant de la matrice M-lI est égal à (1-l)3.
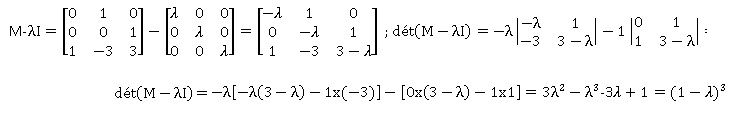
b. Justifier que M admet une seule valeur propre ; déterminer la dimension du sous espace propre associé.
Les valeurs propres de M sont les scalaires tels que dét(M-lI) = 0.
(1-l)3 = 0 admet une seule solution dans R : l = 1. Cette racine est triple.
La matrice M admet une seule valeur propre dont l'ordre de multiplicité est égal à3.
La dimension du sous espace propre associé à cette unique valeur propre est égale à son ordre de multiplicité soit 3.
c. La matrice M est -elle inversible ? La matrice M est-elle diagonalisable ?
M est inversible si et seulement si son déterminant est non nul.
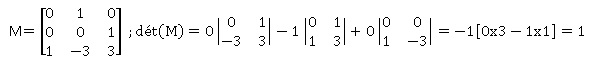
La matrice M est donc inversible.
On a une seule valeur propre triple et M diffère de µI3 avec µ scalaire réel
La matrice M n'est donc pas diagonisable.
2. On pose e1 = i+j+k, e2 = 2i+j.
a. Montrer que B' =(e1, e2, i) est une base de R3.
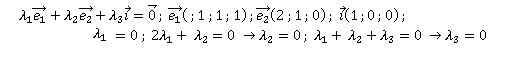
La famille B' est libre ; c'est une base car elle est formée de trois vecteurs en dimension 3.
b. Montrer que la matrice N de l'endomorphisme f dans la base B' est :
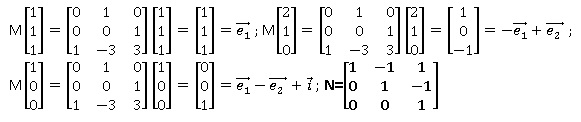
c. Quelle est la matrice P telle que PNP-1 = M ?
PNP-1 P= MP ; PN = MP

3. Montrer que pour tout entier n non nul fn(e2) = -ne1+e2 .
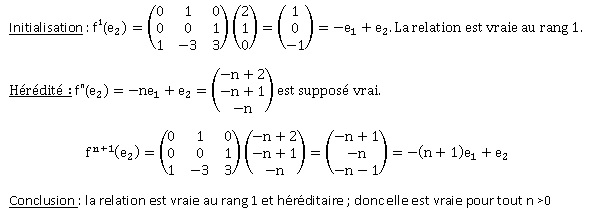
b. On admet que, pour tout entier naturel n, Nn est de la forme suivante. Déterminer les constantes a, b et c.
Pour n = 1 : a+b+c = 1 soit c =1 -a-b.
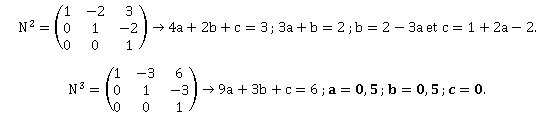
4. Exprimer Mn en fonction de n.
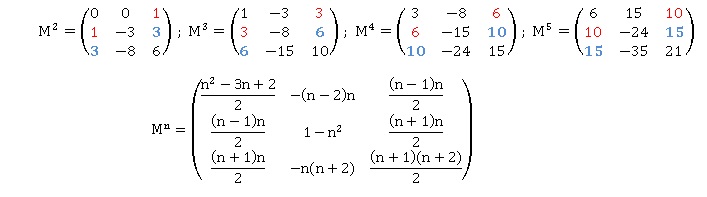
|
|
|
Thermodynamique.(3,5 points)
L’objet du problème est l’étude du refroidissement d'une salle de serveurs.
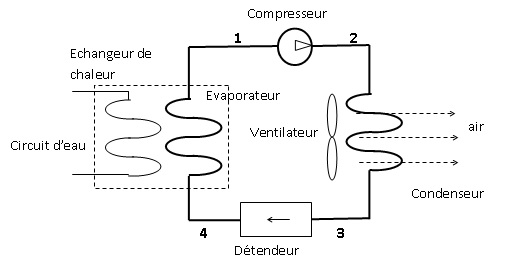
Le fluide subissant le cycle thermodynamique est du fréon. Le circuit est représenté en trait épais.
1, 2, 3, 4 sont les points du circuit correspondant aux entrées et
sorties de chaque élément. Un ventilateur soufflant de l'air sur le
condenseur assure le refroidissement du dispositif et de la salle où
est hébergé le serveur.
L'évaporateur et le circuit d'eau sont mis en contact thermique par un
échangeur de chaleur, représenté en pointillé. Le circuit d'eau est
représenté en trait fin.
La vapeur de fréon est considérée comme un gaz parfait. On désigne
respectivement par P et T sa pression et sa température. On donne les
caractéristiques thermodynamiques du fréon :
Masse molaire M = 121 g/mol.
Chaleur latente massique de vaporisation L = 130 kJ kg-1 à 310 K.
Capacité thermique molaire à pression constante du fréon gazeux : Cp = 49,9 J K-1 mol-1 ; g = Cp / Cv = 1,2.
R = 8,32 J K-1 mol-1.
Au point 1 le fréon est totalement gazeux. P1 = 1,9 105 Pa ; T1 = 272 K.
Au point 2 le fréon est totalement gazeux. P2 = 8,5 105 Pa ; T2 .
Au point 3 le fréon est entierement liquide P3=P2 ; T3 = 310 K.
Au point 4 le fréon est partiellement gazeux. P4 = P1 ; T4.
1. La masse de fréon circculant en un point du circuit en une minute est m = 2,25 kg.
a. En déduire le nombre de moles n de fréon passant en un point du circuit en une minute.
n = m / M = 2,25 / 0,121 =18,595 ~18,6 mol min-1.
b. Quel volume V1 occupe ces n moles de fréon à l'état gazeux sous la pression P1 à la température T1 ?
V1 = n R T1 / P1 =18,595 x8,32 x 272 /(1,9 105)=0,2216 m3 ~221,6 L.
2. On suppose que la transformation réalisée dans le compresseur est adiabatique et réversible. Calculer en litres, le volume V2 occupé par ces n moles de fréon à la pression P2. En déduire T2.
P1V1g = P2V2g ; V2g =(P1 / P2)V1g ; V2 = V1 (P1 / P2)1 /g.
V2 = 221,6 (1,9 / 8,5)1/1,2 = 63,587 ~63,6 L.
T2 = P2V2 /(nR) =8,5 105 x0,0636 /(18,6 x8,32)= 349,4 K.
3. Dans le condenseur, le fréon subit un refroidissement à l'état gazeux de T2 à T3, puis une liquéfaction à la température T3.
a. Calculer la quantité de chaleur Qa échangée par le fréon gazeux , en une minute, lors de ce refroidissement.
Qa = n Cp (T3-T2) =18,595 x49,9 (310-349,4) = -3,65 104 J min-1.
b. Calculer la quantité de chaleur Qb échangée par le fréon, en une minute, lors de sa liquéfaction totale.
Qb = -m L =-2,25 x130 103 = -2,925 105 J min-1.
c. En déduire la quantité de chaleur Q23 échangée par le fréon, en une minute, dans le condenseur pour son refroidissement et sa liquéfaction.
Q23 = -3,65 104 -2,925 105 ~ -3,29 105 J min-1.
4. Dans l'évaporateur, la valeur algébrique de quantité de chaleur Q41 reçue par le fréon, en une minute est Q41 = 240 kJ. En déduire le débit maximal de l'eau, si on veut abaisser la température de celle-ci de 5°C. Ceau = 4180 J K-1 kg-1.
Q41 = Débit Ceau |Dq |; Débit =Q41 / ( Ceau |Dq |) =240 103 / (4180 x5) ~11,5 kg min-1 ou 11,5 L min-1.
|
|
|
|
Electricité. 3 points.
Sortie du transformateur : 800 kVA ; 400 V ; 50 Hz, 3 phases.
On désire alimenter deux moteurs identiques ; pour chaque moteur : Putile = 250 kW ; cos f = 0,75.
1.
Calculer la puissance apparente nécessaire pour alimenter les deux
moteurs fonctionnant au régime nominal, c'est à dire au rendement maxi
de 80 %.
Puissance électrique consommée par chaque moteur au régime nominal : Putile / rendement =250 / 0,80 = 312,5 kW.
Puissance apparente de chaque moteur : S = 312,5 / 0,75 = 416,67 ~417 kVA.
2. Le transformateur de 800 kVA est-il en surcharge ? Justifier.
Puissance apparente des deux moteurs : 2 x416,66 ~ 833 kVA.
Nous compensons cette installation avec une batterie de condensateurs connectée sur le jeu de barres afin d'avoir cos f = 0,92.
3. Calculer la puissance apparente alors appelée.
Les condensateurs ne consomment pas de puissance active.
Puissance apparente de l'installation : S = 312,5 x 2 / 0,92 = 416,67 ~679 kVA.
4. Le transformateur est-il soulagé ? Justifier.
679 est inférieur à 800 ; le transformateur est soulagé.
5. Calculer la batterie de condensateurs à mettre en place pour y parvenir. Vous calculerer la puissance réactive Qc de la batterie de condensateurs nécessaire puis la capacité totale C de cette batterie couplée en étoile.
Puissance réactive des moteurs : (833,32 -6252)½ =551 kvar
Puissance réactive de l'installation : (679,32-6252)½ =266 kvar
|
Puissance active ( kW)
|
Puissance réactive (kvar)
|
Puissance apparente (kVA)
|
Moteurs
|
625
|
551
|
833,3
|
Condensateurs
|
0
|
Qc= 266-551= -285
|
-154
|
Total
|
625
|
266
|
679,3
|
En étoile : C = -Qc / (3V2w) avec w = 2 p f = 6,28*50 =314 rad/s et V = 400 / 3½.
C = 285 103 /(4002*314)~5,7 10-3 F =5,7 mF.
Hydraulique : 3,5 points.
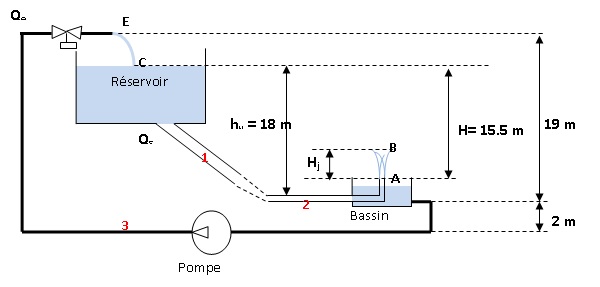
Canalisation 1 : longueur 1,5 km, diamètre 900 mm. Canalisation 2 : diamètre 500 mm.
Canalisation 3 : longueur 1,8 km, diamètre 400 mm.
1.
En considérant le réservoir comme de très grande dimension et donc
en faisant l'hypothèse appropriée sur la vitesse du point C, Vc, calculer la vitesse VA
du jet en sortie de canalisation au niveau du bassin si on néglige les
pertes de charges le long des canalisations 1 et 2 et en considérant un
écoulement laminaire permanent.
Relation de Bernoulli entre A et C : ½reauv2A + PA +reau gzA= ½reauv2c + Pc +reau gzc.
PA = PC = pression atmosphérique.
Vc est voisine de zéro, la surface du bassin étant très grande.
½reauv2A + reau gzA= reau gzc.
½v2A + gzA= gzc ; VA = (2gH)½ =(2 x9,81 x15,5)½ =17,44 ~17,4 m s-1.
2. Calculer alors la hauteur du jet en négligeant les frottements de l'air sur l'eau.
Conservation de l'énergie mécanique de l'eau entre A et B.
½mVA2 = mg HJ ; HJ = 0,5VA2 / g = 0,5 x17,442 / 9,81 ~15,5 m.
Le système devant fonctionner en circuit fermé, il faut transférer
l'eau récupérée vers le réservoir grâce à une pompe hydraulique. Le
débit Qe vaut 65 L / s. ( 0,065 m3 s-1).
3. En prenant le
point D à la surface de l'eau en position la plus défavorable, c'est à
dire avec un bassin presque vide, et le point E en sortie de
canalisation de retour ( à l'air libre), calculer les vitesses en
entrée et en sortie de canalisation de retour en supposant un débit
constant et conservé et un diamètre de canalisation constant sur toute
la longueur.
Le débit étant constant ainsi que le diamètre de la canalisation, la
vitesse de l'eau en E est identique à la vitesse de l'eau en D.
vE = vD= Qe / S avec S = p r2 = 3,14 x0,202 ~0,1256 m s-1.
vE = vD= 0,065 / 0,1256 ~0,517 m s-1.
4. Calculer la
puissance de la pompe en prenant en compte les pertes de charges totale
J du circuit hydraulique ( canalisation de retour ) égales à 18 J
kg-1.
Relation de Bernoulli entre D et E : ½reauv2E + PE +reau gzE- ( ½reauv2D + PD +reau gzD ) =P / Qe -Dp.
P : puissance de la pompe, Qe débit et Dp pertes égales à 18 x reau =1,8 104 J m-3 ( Pa).
PE =PD = pression atmosphérique.
reau g(zE-zD) =P / Qe -Dp.
P =reau g(zE-zD) +Dp) Qe=1000 x9,81 x19 +1,8 104) x0,065 ~13,3 kW.
|
|