Force
de Laplace, concours
officier 1ère classe de la Marine Marchande 2012
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Une
barre de cuivre CD, homogène, de masse m = 0,30 kg, de longueur l =
CD=0,20 m peut glisser sans frottement sur 2 rails métalliques contenus
dans un plan (Q) incliné d’un angle a = 14° sur le
plan horizontal.
Les extrémités supérieures des rails sont reliées à un générateur de
tension continue. La barre CD est perpendiculaire aux rails. L’ensemble
du montage est plongé dans un champ magnétique uniforme B = 0,7 T
orthogonal au
plan (Q) et dirigé vers le haut.
Donner
les caractéristiques de la force électromagnétique F qui s’exerce sur
la tige CD.
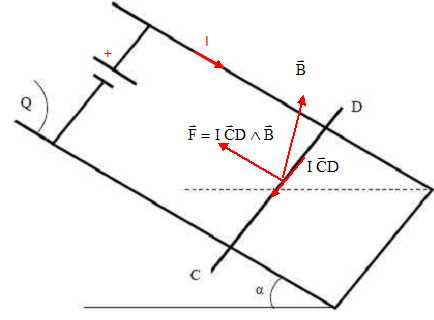
La force de Laplace est perpendiculaire au plan défini par le courant
et le champ. Cette force est contenue dans le plan Q, dirigée vers le
haut. F = I CD B.
Calculer
la valeur du courant que doit fournir le générateur pour que la barre
soit en équilibre.
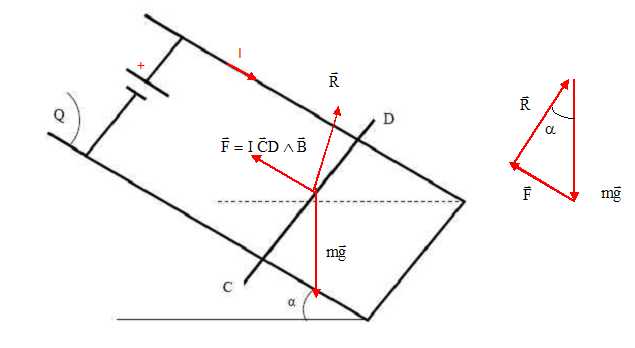
F = I CD B = mg sin a
; I = mg sin a /(CD B) =0,30*10
sin 14 /(0,20*0,70) ~5,2 A.
|
| .
. |
|
|
On modifie le champ magnétique ;
celui-ci est maintenant perpendiculaire au plan horizontal, toujours
dirigé vers le haut avec B = 0,7 T. L’intensité du courant conserve la
valeur trouvée précédemment.
Donner
les caractéristiques de la nouvelle force électromagnétique F’ qui
s’exerce sur la tige CD.
Calculer
le nouvel angle α’ pour que la barre soit toujours à l’équilibre.
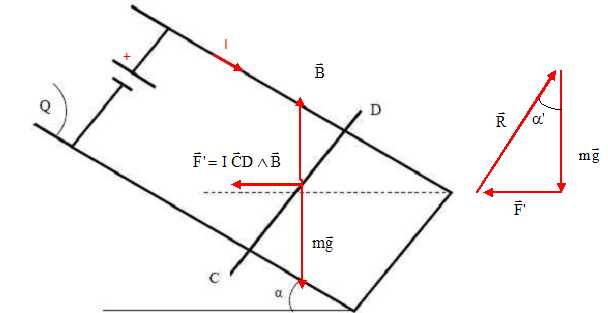
La
force de Laplace est perpendiculaire au plan défini par le courant et
le champ. Cette force est contenue dans le planhorizontal, dirigée vers
la gauche. F = I CD B.
F = I CD B = mg tan a' ; tan a' =I CD B / (mg) =5,2*0,20*0,70 /(0,30*10)
=0,243 ; a'
=13,6°.
|
.
|
|
Deux
rails parallèles, horizontaux et distants de 20 cm, sont
réunis
par un conducteur mobile MN perpendiculaire à ceux-ci, par un rail
conducteur fixe à travers lequel un générateur de f.é.m. E = 1,5 V et de
résistance
interne négligeable, débite un courant électrique. L’ensemble est placé
dans un champ magnétique uniforme vertical ascendant d’induction B =
0,6 T. On suppose que la résistance du circuit est négligeable face à
la résistance r = 2 W du
conducteur mobile MN.
On
maintient le conducteur MN stoppé.
Reproduire
le schéma et représenter la force électromagnétique F. Calculer cette
force électromagnétique F.
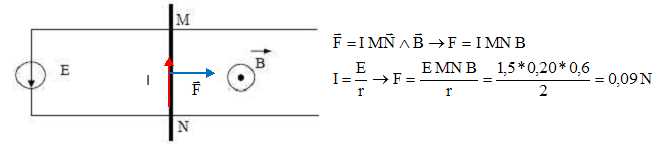
On
relâche le conducteur MN et il se déplace sans frottement
à une vitesse constante v= 1 m.s-1. Calculer :
la
valeur de la f.c.é.m. induite dans le conducteur mobile ;
e = B MN v =0,6*0,2*1 = 0,12 V.
l’intensité
du courant électrique parcourant le circuit ;
Par
ses effets électromagnétiques, cette fem s'oppose à la cause qui lui
donne naisance ; le courant induit i = e/r = 0,12 / 2 = 0,06 A a le
sens contraire à I :
par suite le courant parcourant le circuit est I-i = 1,5/2-0,06 = 0,069
A.
la
force électromagnétique s’exerçant sur le conducteur MN.
F=(E-e)MN B / r = 0,69*0,2*0,6 ~0,083 N.
|
On
considère deux conducteurs parallèles et verticaux, de très grande
longueur, distants de 1 mètre l’un de l’autre dans l’air. Ces
conducteurs coupent un plan (P) qui leur est perpendiculaire aux points
M1 et M2. Le conducteur
de gauche est parcouru par un courant d’intensité I1
égale à 1 ampère.
Calculer
l’excitation magnétique H2 créée par
le courant I1 au point M2.
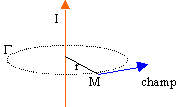
| En tout point de G
le champ magnétique a même module et est tangent à G.
Appliquer
le th. d'Ampère sur le contour G,
cercle de rayon r
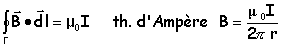
H2
= I / (2pr).
|
|
En déduire
la norme et la direction du champ magnétique B2 existant
en ce point.
|
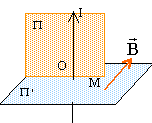
fil
ou cylindre infini parcouru par un courant uniforme
:
|
tout plan
perpendiculaire au fil est plan d'antisymétrie ;
tout plan contenant le fil est plan de
symétrie
invariant par translation le long de l'axe
et invariant par translation le long de laxe :
donc le champ dépend
de la distance OM
B2
= µ0I / (2pr).
|
Le
fil de droite est
traversé par un courant de même sens que I1 et
d’intensité égale à 1 ampère.
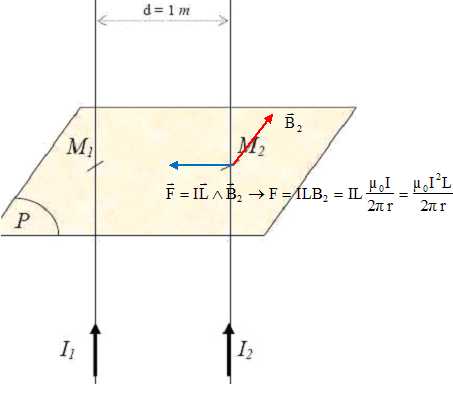
Donner
les caractéristiques, direction et norme, de la force F qui s’exercera
sur une longueur de 1 mètre de ce fil, également répartie de chaque
coté du point M2.
Reproduire
le schéma et représenter le champ magnétique et la force F.
On donne la
perméabilité magnétique de l’air : μ0
= 4p.10-7
H.m-1.rente consommées par
ce récepteur.
A.N : F = 4
p10-7
/ (2p) =2
10-7 N.
|
|
|