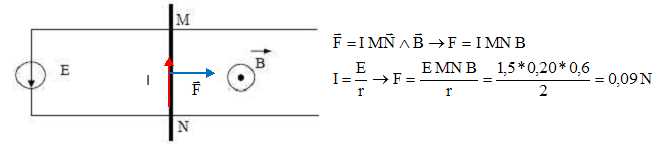Force
de Laplace, récepteur inductif, concours
Marine Marchande 2012 et 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
On
considère deux conducteurs parallèles et verticaux, de très grande
longueur, distants de 1 mètre l’un de l’autre dans l’air. Ces
conducteurs coupent un plan (P) qui leur est perpendiculaire aux points
M1 et M2. Le conducteur
de gauche est parcouru par un courant d’intensité I1
égale à 1 ampère.
Calculer
l’excitation magnétique H2 créée par
le courant I1 au point M2.
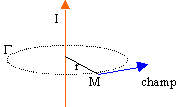
| En tout point de G
le champ magnétique a même module et est tangent à G.
Appliquer
le th. d'Ampère sur le contour G,
cercle de rayon r
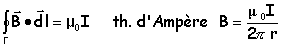
H2
= I / (2pr).
|
|
En déduire
la norme et la direction du champ magnétique B2 existant
en ce point.
|
fil
ou cylindre infini parcouru par un courant uniforme
:
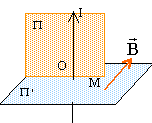
|
tout plan
perpendiculaire au fil est plan d'antisymétrie ;
tout plan contenant le fil est plan de
symétrie
invariant par translation le long de l'axe
et invariant par translation le long de laxe :
donc le champ dépend
de la distance OM
B2
= µ0I / (2pr).
|
Le fil de droite est
traversé par un courant de même sens que I1 et
d’intensité égale à 1 ampère.
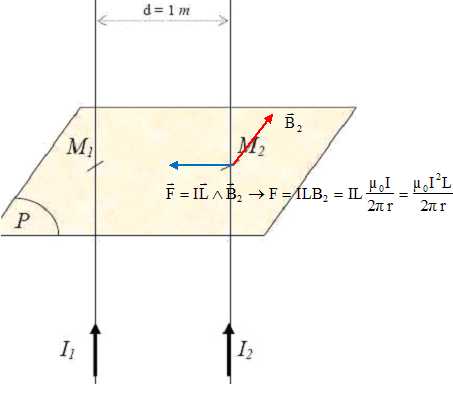
Donner
les caractéristiques, direction et norme, de la force F qui s’exercera
sur une longueur de 1 mètre de ce fil, également répartie de chaque
coté du point M2.
Reproduire
le schéma et représenter le champ magnétique et la force F.
On donne la perméabilité magnétique de l’air : μ0
= 4p.10-7
H.m-1.
A.N : F = 4 p10-7
/ (2p) =2
10-7 N.
|
| .
. |
|
|
.
|
.
|
|
Deux
rails parallèles, horizontaux et distants de 20 cm, sont
réunis
par un conducteur mobile MN perpendiculaire à ceux-ci, par un rail
conducteur fixe à travers lequel un générateur de f.é.m. E = 1,5 V et de
résistance
interne négligeable, débite un courant électrique. L’ensemble est placé
dans un champ magnétique uniforme vertical ascendant d’induction B =
0,6 T. On suppose que la résistance du circuit est négligeable face à
la résistance r = 2 W du
conducteur mobile MN.
On
maintient le conducteur MN stoppé.
Reproduire
le schéma et représenter la force électromagnétique F. Calculer cette
force électromagnétique F.
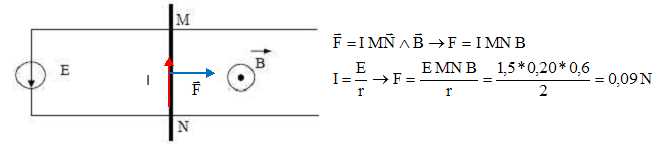
On
relâche le conducteur MN et il se déplace sans frottement
à une vitesse constante v= 1 m.s-1. Calculer :
la
valeur de la f.c.é.m. induite dans le conducteur mobile ;
e = B MN v =0,6*0,2*1 = 0,12 V.
l’intensité
du courant électrique parcourant le circuit ;
Par
ses effets électromagnétiques, cette fem s'oppose à la cause qui lui
donne naisance ; le courant induit i = e/r = 0,12 / 2 = 0,06 A a le
sens contraire à I :
par suite le courant parcourant le circuit est I-i = 1,5/2-0,06 = 0,069
A.
la
force électromagnétique s’exerçant sur le conducteur MN.
F=(E-e)MN B / r = 0,69*0,2*0,6 ~0,083 N.
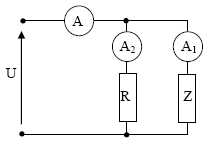
Soit
le circuit électrique suivants, dans lequel R représente une résistance
pure de 5 W
et Z un récepteur dont on veut connaître les caractéristiques
principales au moyen d’un ampèremètre branché successivement en A, A1
et A2. Le circuit étant alimenté à la fréquence
de 50 Hz, on relève les valeurs respectives suivantes : I = 12,0 A ; I1
= 6,0 A et I2 = 6,8 A.
Déterminer
la puissance absorbée par la résistance pure et en déduire la valeur de
la tension d’alimentation U.
Puissance Joule absorbée par R : PJ = RI22
=5*6,82 =231,2 W ; PJ = UI2
; U = 231,2 / 6,8 =34 V.
Déterminer
le diagramme de Fresnel sur les intensités et en déduire le déphasage
de l’intensité sur la tension du récepteur Z.
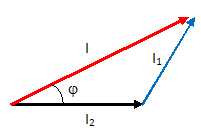
I12 =I2+I22-2I
I2 cos j
; 6,02 = 12,02 +6,82-2*6,8*12
cos j ; 154,24 =163,2 cos j ; cos j =0,945 ; j =19,07 ~19,1°.
I2 et U sont en phase. I est en avance de j = 19,1° sur U.
Déterminer
le facteur de puissance et la puissance absorbée par le récepteur Z.
cos f =
cos 19,07 =0,945 ; Ptotale =UI cos j =34*12,0*0,945
~385,6 W.
Puissance absorbée par le récepteur Z : PZ =Ptotale-PJ=
385,6-231,2 = 154,4 W
Déterminer
l’impédance du récepteur Z et en déduire la valeur de la résistance r
et de l’inductance L composant ce récepteur.
Z = U/I1 = 34/6,0 =5,67 ohms.
r = PZ/I12
= 154,4 / 62 =4,29 ohms.
Z2 = r2 +(Lw)2 avec
w
= 2 p f =
2*3,14*50=314 rad/s.
(Lw)2
=Z2 -r2 =5,672
-4,292 =13,74 ; Lw =3,71 ; L =
3,71/314 = 0,0118 H =11,8 mH.
|
Un
récepteur inductif est alimenté par une tension alternative
sinusoïdale, notée U, de valeur efficace égale à 220 V et de fréquence
égale à 50 Hz tel que représenté sur le schéma ci-dessous.
On donne : L = 0,15 H ; R = 50 W.
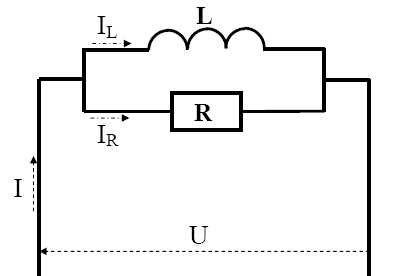
Calculer
la valeur de l’intensité des courants IL et IR ainsi que
leur déphasage par rapport à la tension U.
IR =U/R =220/50 =4,4 A. IR est en phase avec la tension U.
IL = U/(Lw) avec w = 2 p f = 2*3,14*50 = 314 rad/s.
IL =220/(0,15*314) =4,67 ~4,7 A. IL st en avance de ½p sur U.
En déduire l’intensité du courant I et son déphasage par rapport à
la tension U.
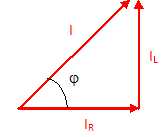
I=(I2R+I2L)½ =(4,42 +4,672)½ =6,416 ~6,4 A ; tan j =IL/IR =4,67/4,4 =1,061 ; j =46,7°.
Calculer les puissances active, réactive et apparente consommées par
ce récepteur.
R consomme de la puissance active : P =RIR2 = 50*4,42 =968 W.
La bobine consomme de la puissance réactive : Q =U sin j =220*6,4 sin 46,7 =1,025 103 ~1,03 103 var.
Puissance apparente S = UI =220*6,416 =1411,5 ~1,41 103 VA.
On veut supprimer la puissance réactive consommée en insérant une
capacité en parallèle à ce récepteur.
Calculer la valeur, notée C, de cette capacité et la valeur de l’intensité du courant I qui sera fourni par la source
au nouveau montage.
Puissance réactive du condensateur : -C w U2
=-1025 ; C =1025/(314*2202) =6,74 10-5 F.
U et I sont en phase et la puissance active reste inchangée : P = UI ; I = P/U =968/220 =4,4 A.
|
|
|