Mathématiques,
fonctions, nombres complexes, intégrales,
concours Puissance 11. 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Exercice 1. bases en analyse.
a. La dérivée de f(x) = x / ex est f '(x) = (x-1) / ex. Faux.
On pose u = x ; v =ex ; u' = 1 ; v' = ex.
(u'v-v'u) / v2 = (ex-xex) / e2x = (1-x) /ex.
b. Quand x tend vers l'infini, la limite de x /ex est l'infini. Faux.
Par croissance comparée x / ex tend vers 0 quand x tend vers l'infini.
Soit g une fonction définie sur ]0 ; +oo[ telle que, pour tout x >0 : 1 /x < g(x) < x/ex.
c. Quand x tend vers +oo, la limite de g(x) est égale à zéro. Vrai.
d. Soit (Un) la suite définie, pour tout entier naturel n non nul, par un = ln(1/n)..
La suite converge vers zéro. Faux.
Quand n tend vers l'infini, 1/n tend vers zéro et ln(1/n) tend vers moins l'infini.
Exercice 2 . Bases de géométrie.
Soit P et Q les plans d'équations respectives :
(P) : 2x+y+z=2 ; (Q) : x+y-z=0
a. L'intersection des deux plans a pour équation x+2z=2. Vrai.
Les coordonnées d'un point M(x, y z) appartenant à leur intersection vérifient :
2x+y+z=2 et x+y-z=0.
2x-x+y-y+z+z=2 soit x+2z=2.
b. Soit (D) la droite dont une représentation paramétrique est :
x=t+3 ; y = -t-1 ; z = 2 avec t réel.
(D) est perpendiculaire au plan (R) d'équation x-y+2z=0. Faux.
Coordonnées du vecteur directeur de la droite (D) : (1 ; -1 ; 0).
Coordonnées du vecteur normal au plan (R) : (1 ; -1 ; 2).
Le produit scalaire de ces deux vecteurs n'est pas nul, (D) et (R)ne sont pas perpendiculaires.
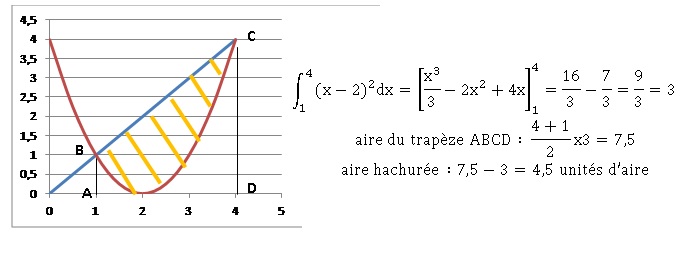
c. Sur le graphe ci-contre, nous avons tracé les courbes représentatives des fonctions f(x) = x et g(x) = (x-2)2. L'aire du domaine hachuré est égal à 4,5 unités d'aire. Vrai.
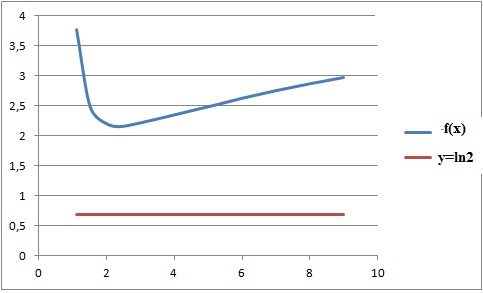
d. La courbe représentative de la fonction fdéfinie sur ]1 ; +oo[ par f(x) = ln[(2x2-x+3) / (x-1)]
admet une asymptote horizontale d'équation y = ln 2. Faux.
Exercice 3. Lecture graphique.
f
est une fonction définie et dérivable sur [−3 ; 5] de courbe
représentative (C). On donne ci-dessous la courbe (Γ) représentative de
sa fonction dérivée f ′.
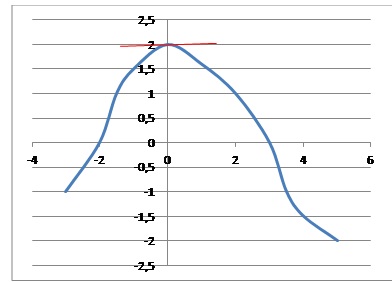
a. (C) admet une tangente horizontale en x = 0. Faux.
La courbe (G) admet une tangente horizontale en x=0.
b. f admet un minimum relatif en x = −2. Vrai.
f '(x) s'annule et change de signe en x=-2.
c. La fonction f est strictement décroissante sur [0 ; 5]. Faux.
f '(x) est positive entre 0 et 3 : f(x) croissante.
f '(x) est négative entre 3 et 5 : f(x) décroissante.
d. Les tangentes à (C) aux points d’abscisses x = -1,5 et x=2 sont parallèles. Vrai.
f '(-1,5) = f '(2) = 1. Les tangentes en x=-1,5 et x=2 ont même coefficient directeur.
.
Exercice 4. Suite définie par un algorithme.
variables
u est du type nombre
n est du type nombre
k est du type nombre
Lire n
u prend la valeur 2
k prend la valeur 0
Tant que k < n faire
k prend la valeur k +1
u prend la valeur u +2*(k −1)+1
fin tant que
Afficher u.
a. u3=11. Vrai.
k
|
0
|
1 |
2
|
3
|
u
|
2
|
2+2(1-1)+1=3
|
3+2(2-1)+1=6
|
6+2(3-1)+1=11
|
b. Pour tout entier naturel n, un+1 = un +2n +1. Faux.
u1=2+2n-1 =3 ; u2=u1+2n-1=6 ; u3=u2+2n-1=6+6-1=11. u4 = u3 +2n-1 =11+8-1=18.
c. La suite (un) est strictement croissante.Vrai.
d. Pour tout entier naturel n, un = n2 +2. Vrai.
|
| .
. |
|
|
Exercice 5. Bases sur les complexes.
Le plan complexe est rapporté à un repère orthonormal direct. On considère les nombres complexes suivants :
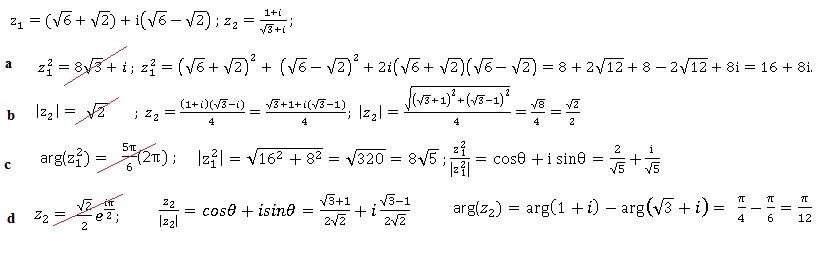
Exercice 6. Bases de logique.
Le plan complexe est muni du repère orthonormé direct . x et y sont deux nombres réels et z est le nombre complexe x +iy.
a. La négation de la proposition : « x >0 et y >0 » est la proposition « x < 0 et y < 0 ». Vrai.
b. Si x = y alors arg(z)= p/4 modulo 2p. Faux.
C'est vrai si x et y sont positifs ; si x et y sont négatiifs, arg( z) = 5p/4(2p).
c : La réciproque de la proposition précédente est vraie. Vrai.
d : On suppose z différent de 0. Si z = 1 / z, alors x = 0 ou y = 0. Faux.
1/z = 1/(x+iy) = x-iy / (x2+y2) = x + iy.
x2+y2= 1 et y = 0 soit x = ±1 et y = 0.
Exercice 7. Calcul de limites.
a. la fonction f(x) = x sin (x) n'a pas de limite quand x tennd vers l'infini. Vrai.
sin(x) est compris entre -1 et +1.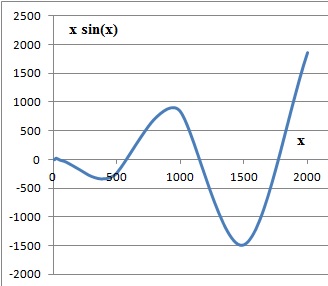
b. Quand x tend vers l'infini, la limlite de (cos(x) +2) / (cos(x)+x) = 1. Faux.
Au voisinage de l'infini cos (x) est négligeable devant x. Le
dénominateur tend vers l'infini et le numérateur est compris enntre 1
et 3. La limite de la limlite de (cos(x) +2) / (cos(x)+x) =0 quand x tend vers l'infini.
c. Quand x tend vers -oo, la limite de (ex+3x) / (x+1) =0. Faux.
Au voisinage de -oo, ex est nul : (ex+3x) / (x+1) est équivalent à 3x / (x+1) = 3 / (1+1/x).
Au voisinage de -oo,1/x est nul ; la limite de (ex+3x) / (x+1) est égale à 3 quand x tend vers-oo.
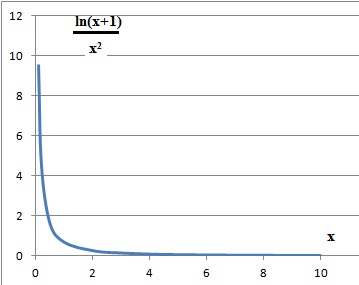
d. La limite de ln(1+x) / x2 =1 quand x tend vers 0. Faux.
Au voisinage de zéro, ln(1+x) est équivalent à x -0,5 x2 +x3 /3.
ln(1+x) / x2 est équivalent à : 1/x -0,5 +x/3.
|
|
|
|
8. Calcul d'intégrales
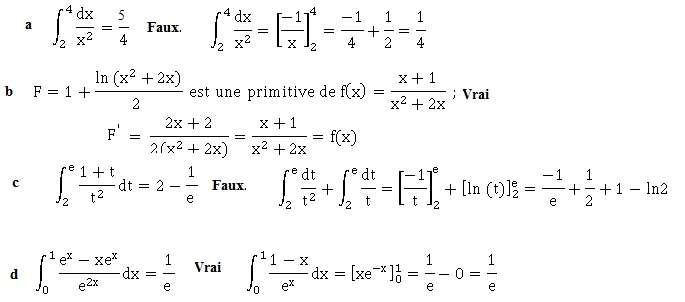
9. Transformation complexe.
Le
plan complexe est rapporté à un repère orthonormal direct. Soit f la
transformation du plan complexe qui, à tout point M d’affixe z, associe
le point M′ d’affixe z′ = (1+i)z +1.
.
a. L’image, par f , du point B d’affixe 2 est le point C d’affixe 3+2i. Vrai.
z = 2 ; z' = 2 (1+i)+1 = 3 +2i.
b. Le point A d’affixe i est le seul point invariant par f. Vrai.
Pour un point invariant : z = z' ; z = (1+i)z+1 ; -1 = z(1+i-1) ; -1 = z i ; z = -1 / i = i.
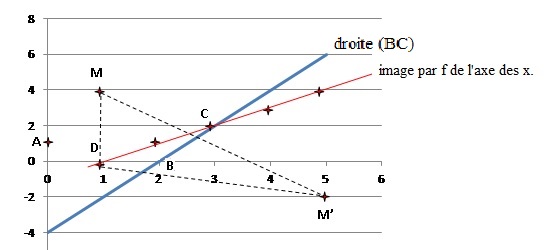
c. L’image, par f , de l’axe des réels est la droite (BC). Faux
Equation de l'axe des réels : y =0.
z = x+iy avec x et y réels ; z = x.
z' = (1+i) x+1 ; z' = x+1 +ix.
Equation de la droite (BC) : y = ax +b.
B(2 ; 0) appartient à cette droite : 0 = 2a+b.
C(3 ; 2) appartient à cette droite : 2 = 3a+b ; a = 2 et b = -4 ; y =2x-4.
d. Soit D le point d’affixe 1. Pour tout point M distinct de A et de D, le triangle DMM′est isocèle en M. Faux.
M(x ; y ) ; D(1 ; 0) ; DM = [(x-1)2 +y2]½.
z' = (1+i)(x+iy) +1 = x-y+1 +i(x+y). M'( x-y+1 ; x+y).
MM' = [(1-y)2+x2]½.
|
|
|
|
Exercice 10. Loi normale.
Dans tout l’exercice, on suppose T une variable aléatoire qui suit la loi normale N(5 ; s2) avec μ et s deux entiers naturels.
N( 3 < T < 7) = 0,68.
a. μ = 5 et s = 4. Faux.
On pose Y = (7-5) / s = 2 /s.
F(Y < 2 / s) = 1-(1-0,68) / 2 = 0,84. Les tables donnent 2 / s ~1,0 soit s ~2.
b. N( 1 < T < 9) = 0,8. Faux.
On pose Y = (9-5) / s = 4 / 2 = 2.
Les tables donnent F(Y<2) =0,977 ; N( 1 < T < 9) =1-(1-0,977) x2 = 0,954.
c. N( 7 < T < 9) = 0,135. Vrai.
On pose Y = (7-5) / s = 2 / 2 = 1. Les tables donnent F(Y<1) =0,841 ;
On pose Y' = (9-5) / s = 4 / 2 = 2. Les tables donnent F(Y'<2) =0,977 ;
N( 7 < T < 9) =0,977 -0,841 =0,136.
d. On admet, dans cette question, que P(T ∈ [μ−2s ; μ+2s]) ≈ 0,95. P(T < 9) ~ 0,975. Vrai.
On pose Y = (9-5) / s = 4 / 2 = 2. Les tables donnent F(Y<2) =0,977.
Exercice 11. Nombres complexes et géométrie.
Le
plan complexe est muni d’un repère orthonormé direct. À chaque point M
d’affixe z = x+iy, non nul, on associe l’unique point M′ d’affixe z′ =
x' + iy' tel que :
z' = [(x-iy) / |z| ]2.
a. On a x' = (x2-y2) / (x2+y2) et y' = 2xy /(x2+y2). Faux.
x' + iy' = (x-iy)2 / (x2+y2) = (x2-y2-2ixy) / (x2+y2).
b. M′ appartient à l’axe des ordonnées si et seulement si M appartient à la droite d’équation y = x privée de O. Faux.
Si x = y : M(x ; x) ; M'( 0 ; -1).
Si M' appartient à l'axe des ordonnées : x'=0 : M'(0 ; y ) ; x2-y2 = 0 soit x = ±y.
c. M′ est un point du cercle trigonométrique. Vrai.
x'2 +y'2 = [ (x2-y2)2 +(-2xy)2 ] / (x2+y2)2 =(x2+y2)2 / (x2+y2)2 = 1.
d. M′ a pour affixe −1 si et seulement si z = i ou z = −i. Faux.
Si M' a pour affixe -1 : x' = 0 ; x2-y2 = 0 soit x = ±y.
y' = -1 ; 2xy =(x2+y2) ; 2xy = 2x2 ; y = x.
Exercice 12. Etude d'une fonction logarithme.
On considère la fonction f définie sur R par f (x) = ln(x2 +x +1) de courbe représentative (C ).
a. f est croissante sur R. Faux.
f '(x) = (2x+1) / (x2 +x +1).
Si x < - 0,5, f '(x) est négative et f(x) est strictement décroissante.
Si x > - 0,5, f '(x) est positive et f(x) est strictement croissante.
Si x = -0,5, f '(x) est nulle et f(x) admet un minimum égal à : f(-0,5) = ln(0,25 -0,5 +1) = ln (0,75).
b. (C ) admet une unique asymptote verticale. Faux.
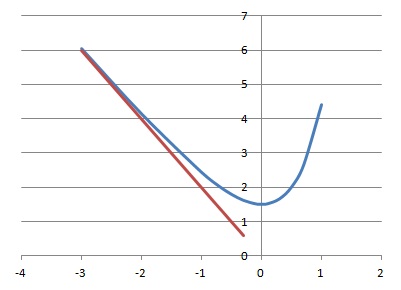
c. Pour tout x réel, f (x)>ln(3/4). Vrai.
d. Il existe deux points de (C ) ayant une tangente à (C ) parallèle à la droite (Δ) d’équation y = x −ln7. Vrai.
Le coefficient directeur des tangentes doit être égal à 1.
f '(x) = (2x+1) / (x2 +x +1) = 1 ; 2x+1 = x2 +x +1 ; x2 -x = 0 soit x = 0 et x = 1.
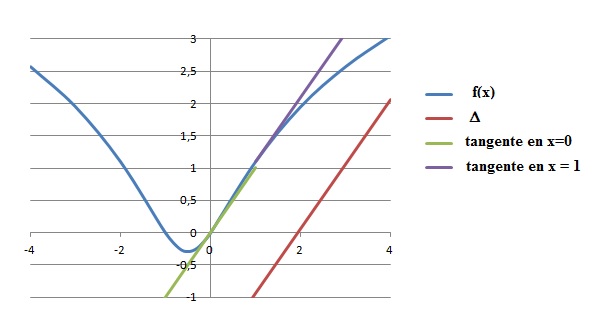
13. Etude d'une fonction exponentielle.
Soit f la fonction définie sur R par f (x) =0,5 e2x+ex-2x
On désigne par C sa représentation graphique dans un repère orthonormé du plan.
a. Pour tout réel x, on a : f ′(x) = (ex −1) (ex +2). Faux.
f '(x) =ex+ex-2 = 2(ex-1).
f '(x) est négative si x <0 et f(x) est strictement décroissante.
f '(x) >0 si x >0 et f(x) est strictement croissante.
f '(x) = 0 si x=0 et f(x) présente un minimum égal à f(0) = 1,5.
b. Pour tout réel x, on a : f (x) >1,5. Faux, il faudrait écrire f(x) >1,5.
c. C admet l’axe des abscisses comme asymptote horizontale en +oo. Faux.
d. Quand x tend vers -oo, f(x) tend vers + oo. Vrai.
Au voisnage de -oo, les termes en exponentielle sont nuls et f(x) est équivalente à -2x.
14. probabilités conditionnelles.
Un joueur effectue des parties successives d’un jeu vidéo.
• La probabilité qu’il gagne la première partie est de 0,2.
• S’il gagne une partie, la probabilité de gagner la suivante est égale à 0,7.
• S’il perd une partie, la probabilité de gagner la suivante est égale à 0,5.
Pour tout entier naturel n non nul, on note :
• Gn l’évènement : « le joueur gagne la n-ième partie » ;
• pn la probabilité de l’évènement Gn.
a. p2 = 0,54. Vrai.
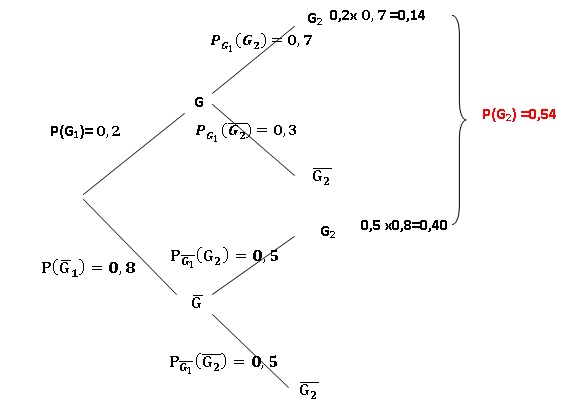
b. Le joueur gagne la deuxième partie. La probabilité qu’il ait perdu la première est 0,6. Faux.
c. Pour tout entier naturel n non nul, on a pn+1 =0,2 pn +0,5. Vrai.
Initialisation : p1 = 0,2 ; p2=0,2 x0,2 +0,5 = 0,54.
Hérédité : supposons l'hypothsèse vrai au rang k : pk =0,2 pk-1 +0,5.
pk+1 = 0,7 pk + 0,5 x(1-pk)=0,3 pk+0,5.
Conclusion : La propriété étant vraie au rang 1 et héréditaire, alors la propriété est vraie.
Pour le d., on donne l’algorithme ci-dessous :
Variables
n est du type nombre
p est du type nombre
i est du type nombre
Lire n
p prend la valeur 0,2
Pour i allant de 2 à n
Début pour
p prend la valeur 0,2 xp +0,5
Fin pour
Afficher p.
d. Si on teste le programme pour n = 5 alors cet algorithme restitue la probabilité que le joueur gagne la cinquième partie. Vrai.
15. Différentes lois de probabilités.
Les quatre questions sont indépendantes.
a. Soit t > 0. Si X suit une loi uniforme sur [0 ; t ] telle que p(X < 5) = 0,4 alors t = 20. Faux.
p(X<5) = (5-0) / (t-0) = 0,4 ; t = 5/0,4 =12,5.
b. Soit n entier naturel non nul. Si X suit une loi binomiale B(n ; 0,3) d’espérance 12, alors n = 40. Vrai.
E(X) = n p = 12 ; n = 12 / 0,3 = 40.
c. Si X suit une loi exponentielle de paramètre l= 2×10−3, alors E(X) = 5000. Faux.
E(X) = 1 /( 210-3) = 500.
d. On considère A et B deux évènements d’une même expérience aléatoire tels que p(A) non nul et p(B) non nul. Si PB (A)= PA(B), alors p(A)= p(B). Vrai.
16. Repérage dans un cube.
On rappelle que :
- Le plan médiateur d'un segment est le plan passant par le milieu de ce segment tout en lui étant perpendiculaire.
- Si M est un point de l’espace et (P) un plan de l’espace, on appelle
distance du point M au plan (P) la plus petite distance d entre le
point M et un point H du plan (P).
L'arête du cube est égale à 1.
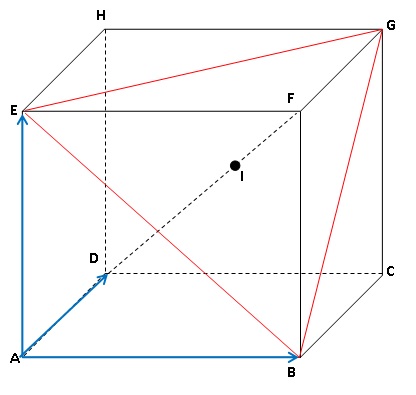
a) (GDF) est le plan médiateur du segment [EB]. Vrai.
b) Le plan (BEG) a pour équation : x – y + z = 1. Vrai.
Equation de ce plan : ax +by +cz =d.
B(1 ; 0 ; 0) appartient à ce plan :a=d.
E(0 ; 0 ; 1) appartient à ce plan : c = d.
G(1 ; 1 ; 1) appartient à ce plan : a+b+c=d.
b+c = 0 ; b=-c =-a ; d'où ax -ay+az =a ; x-y+z=1.
c) I( 2/3 ; 1/3 ; 2/3 ) est le point d’intersection de la droite (DF) avec le plan (BEG). Vrai.
Les coordonnées de I vérifient l'équation du plan (BEG) : 2/3 -1/3 +2/3 = 1
D(0 ; 1 ; 0) ; F( 1 ; 0 ; 1) ; Coordonnées du vecteur directeur de cette droite : (1 ; -1 ; 1)
Equation paramétrique de la droite (DF) :x = t+a ; y = -t +b ; z = t+c.
(DF) passe par D : a = 0 ; b = 1 ; c = 0.
Par suite : x=t ; y = -t+1 ; z = t.
Repport dans l'équation du plan : t -(-t+1)+t =1 ; 3t -1=1 ; t = 2/3.
Coordonnées du point d'intersection de la droite (DF) et du plan (BEG) : 2/3 ; 1/3 ; 2/3.
d) La distance du point D au plan (BEG) est égale à 3½ / 3. Faux.
d = |-yD -1| / (12+(-1)2+12)½=2 / 3½.
|
|