Mathématiques, complexes, intégration, géométrie dans l'espace, concours Avenir 2016

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .
.
.


Nombres complexes.
29. On considère le nombre complexe z = 4+4i, alors un argument de l'opposé de ce nombre complexe conjugué  est, à 2p près :
a. p /4 ;  b. - p /4 ;  c. -3p /4. d. 3p /4. Vrai.


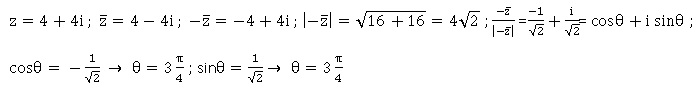
 30. On considère le nombre complexe z = 3 (sin q +i cos q), alors un argument de z, à 2p près, est :
a. q ; b. p/2-q Vrai ; ; c. q+p ;  d. q-p.
z = 3(cos(p/2-q) +i sin(p/2-q).

31. On considère le nombre complexe z = -2 exp(2ip/3) alors un argument de z', à 2p près est :
a : 5p/12 ; b : -5p/12 ;  c : 7p/12 ; d : p/12 Vrai.


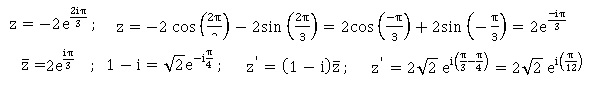
 32. Dans C le trinôme z2-2z+5 admet pour racines :
a : 1+2i et -1-2i ; b : 1+4i et 1-4i ; c : 1+2i et 1-2i Vrai ; d : 1+4i et -1-4i.
Discriminant D = b2-4ac=4-20 = -16 = 16i2.
Solutions : z1 =(2+4i) / 2 = 1+2i et z2=(2-4i)/2 = 1-2i.

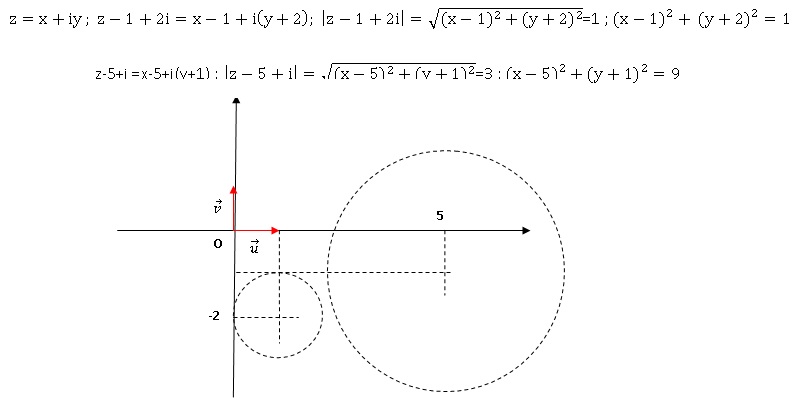
33. On se place dans le plan complexe muni d'un repère orthonormé et on considère l’ensemble E des points M d’affixe z appartenant à C tels que |z-1+2i| =1 et |z-5+i|=3 .
a : E est la réunion de 2 droites.
b : E est la réunion de 2 cercles.
c : E est l’intersection non vide de 2 cercles.
d : Aucune des 3 réponses précédentes n’est exacte. Vrai.
.
.





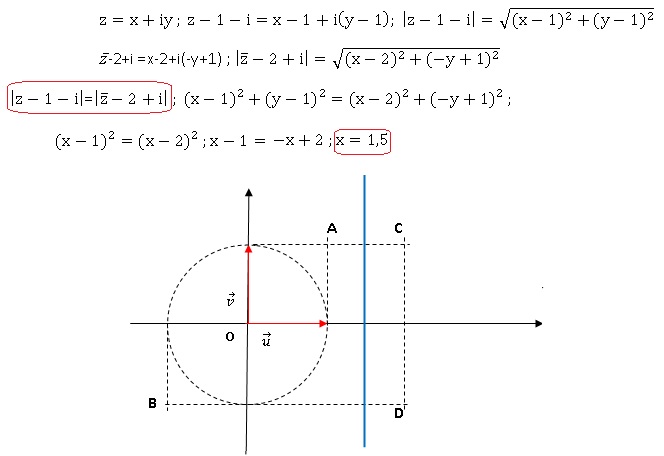
34. On se place dans le plan complexe muni d'un repère orthonormé et on considère les points A, B, C et D d'affixes respectives 1+i, -1-i, 2+i et 2-i. On note E l'ensemble des points d’affixe tels que .
a : E est la droite (AC).
b : E est la médiatrice de [AC]. Vrai.
c : E est la droite(BC)
d : E est la médiatrice de [AD].


35. On se place dans le plan complexe muni d'un repère orthonormé et on considère les pointsM  d'affixe z tels que z2+3i est un nombre imaginaire pur ; ces points sont situés sur :
a : une droite.
b : les axes du repère.
c : un cercle.
d : la réunion de deux droites différentes des axes du repère. Vrai.
z =x+iy ; z2 =x2-y2+2ixy d'où  x2-y2=0 ; y = ±x .

36. On se place dans le plan complexe muni d'un repère orthonormé et on considère l’ensemble E des points M d’affixez tels que l'argument de (z+4i) =p/4 à 2p près. Alors :
a : E est une droite.
b : E est la réunion de 2 droites.
c : E est une demi-droite. Vrai.
d : E est la réunion de 2 demi-droites non parallèles.
z = x+iy ; z+4i= x+i(y+4) = cos q + i sin q avec q appartenant à [0 ; p/2 ].
 tan q >0 ;  y+4 / x =p/4 ; y =  p/4 x-4.

Intégration.
 37.
b. Vrai.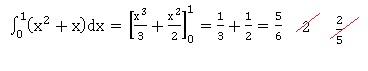
d. Aucune des réponses précédentes.

On considère la fonction définie sur [1 ; 3 ] représentée ci dessous :


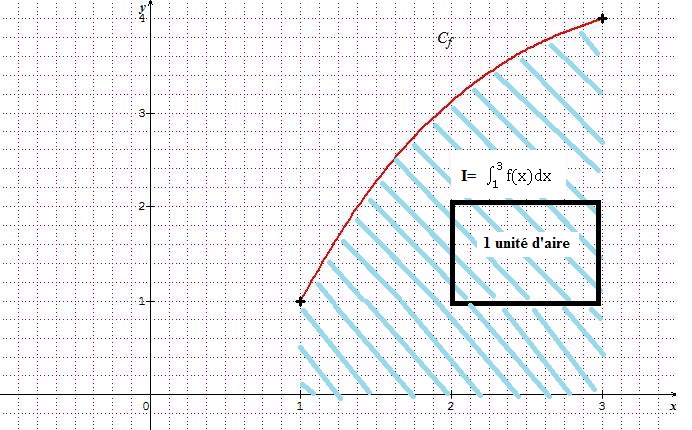
38. a. 3 < I < 4  ; b. 4< I < 5 ; c. 5 < I <6 Vrai ; d.  6 <I <7.

39.  On note m la valeur moyenne de f sur [1 ; 3 ], alors :
a. m=2,5 ; b. m=2 ; c. m<2,5  ; d. m > 2,5 Vrai.
m = aire hachurée  / (3-1) = aire hachurée  / 2 ; 2,5 < m < 6.









Géométrie dans l'espace.
40.  On se place dans l'espace muni d'un repère orthonormé. On considère la droite(d) de représentation paramétrique suivante
x=1+t ; y = -1+3t ; z = 2-t où t appartient à R, alors (d) passe par le point de coordonnées :
a. (1 ; 3 ; -1). b. (1 ; -1 ; 0) ;  c. (0 ; -4 ;-3 ) ; d.(4 ; 8 ; -1). Vrai.
Equation de la droite (d) :-2x +y +z = -2-2t-1+3t+2-t ; -2x+y+z = -1.
 Seul le point de coordonnées  (4 ; 8 ; -1) vérifie cette équation.

41.On se place dans l'espace muni d'un repère orthonormé. On considère le planP d’équation cartésienne 2x-3y+z+1 =0 ;  alors admet pour vecteur normal le vecteur de coordonnées :
a. (6 ; 3 ; 3) ; b. (4 ; -6 ; -2) ; c. (8 ; -12 ; 4) Vrai ; d. (-6 ; 9 ; 2).
Soient  A (0 ; 0 ; -1), B( -½ ; 0 ; 0) et C(1 ; 1 ; 0) des points du plan P.

42. On se place dans l'espace muni d'un repère orthonormé. On considère les deux vecteurs :

Réponse d.

43. On se place dans l'espace muni d'un repère orthonormé. On considère le plan P d’équation cartésienne x-2y+z=3 et le plan P' d’équation cartésienne 2x-y+3z+4=0 . L'intersection de P et P' est :
a.vide ; b. réduite au point A(-5/3 ; 2 /3 ; 0) ;
c. égale à la droite (d) d'équation paramétrique x = -5/3 +5t ; y = 2/3-t ; z = -7t où t est réel ;
 d. Aucune des trois réponse précédente n'est exacte. Vrai.
Les vecteurs normaux à ces deux plans ont pour coordonnées : (1 ; -2 ; 1) et (2 ; -1 ; 3). Ils ne sont pas colinéaires. Les deux plans se coupent donc selon une droite représentée par :


44. On se place dans l'espace muni d'un repère orthonormé. On considère les trois vecteurs suivants :
a. Ces trois vecteurs sont colinéaires ; b. Ces trois versteurs sont non coplanaires. Vrai.
c. Ces trois vecteuurs sont coplanaires. Vrai ; d. Aucune des trois réponses n'est exacte.



On se place dans l'espace muni d'un repère orthonormé. On considère le cube de côté 1. Soit I le milieu de [A'B'].


  

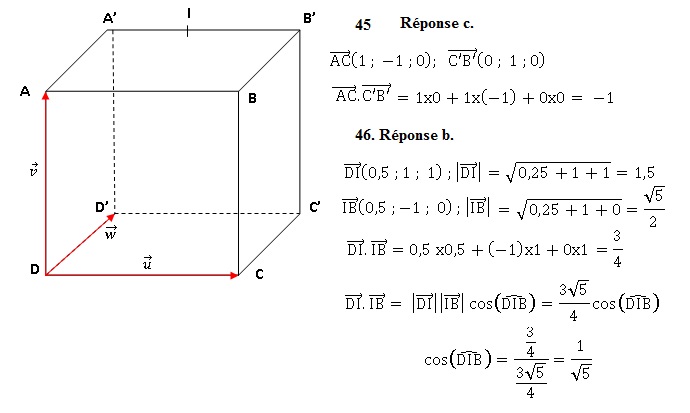
menu