Mathématiques,
suites, logique, fonctions exponentielle et logarithme,
concours Avenir 2016
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Suites.
1. On considère la
suite géométrique (un) de raison q=0,5 et u4=32.
Alors pour tout n entier :
a. un =
32 +(n-4) / 2.
u4 = u0 x (0,5)4 =32 ; un
= u0 x (0,5)n =u0 x (0,5)4
x0,5n-4 =32 x (0,5)n-4.
b. un = 32 x (0,5)n.
c. un =
32 x (0,5)n-4. Vrai.
d.
un = 32 + (0,5)n-4.
2. On considère les deux suites (un)
et (uv) définies par u0=5 ; un+1 =
0,25(3un+vn) et v0=5
; vn+1 = (un+5vn)/6 . On admet que (un)
converge vers l1 relet que (vn) converge vers l2
réel , alors :
a. l1=l2.
Vrai.
b. l1<l2.
c. l1>l2.
d. On ne dispose pas assez
d'informations pour comparer l1 et l2.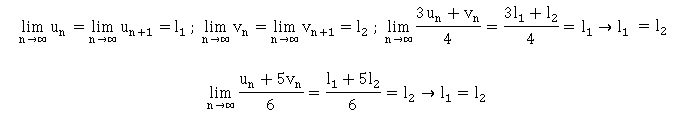
3. On considère une
suite (un) strictement croissante de premier terme u0
=2 et la suite (vn) définie pour tout n entier pa
vn = -2 /(1-3un) . Alors la suite est (vn)
:
a : monotone et
croissante.
b : monotone et
décroissante. Vrai.
c : non monotone
d : Aucune des 3
réponses précédentes n’est exacte.
vn
=-2 /(1-3un) ; vn+1
=-2 /(1-3un+1) ; un+1 >un
entraîne 1-3un+1 <1-3un entraîne 1/(1-3un+1 ) > 1 (1-3un )
entraîne : -2/(1-3un+1 ) < -2 (1-3un )
On
considère la suite (un) définie par u0=7 et un+1=f(un)
pour tout n entier, où est la fonction définie sur [4 : +oo[
représentée ci-dessous :
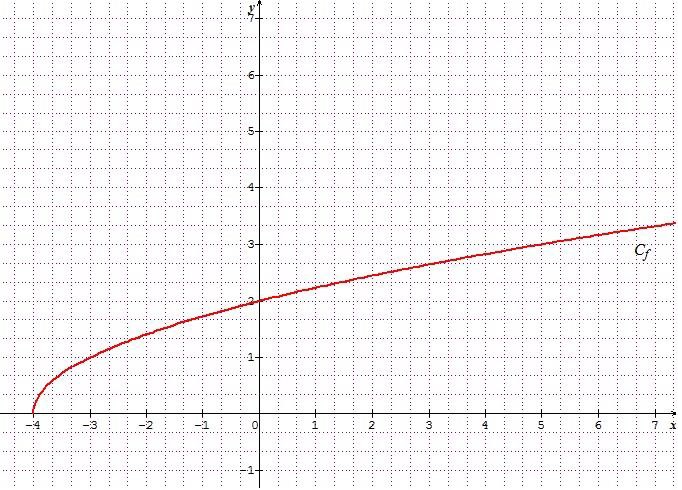
4. La suite (un) est :
a : monotone et
croissante.
b : monotone et
décroissante. Vrai.
c : non monotone.
d : Aucune des 3
réponses précédentes n’est exacte.
u1 = f(u0) = f(7) ~3,33 ; u2 = f(u1)
~2,7 ; u3 = f(u2)
~2,65 ;
u4 = f(u3) ~2,55.
5.
La suite (un):
a : converge vers 2.
b : diverge vers
+oo.
c : converge vers
-4.
d : converge vers l
appartenant à [2 ; +oo[. Vrai.
Logique.
6. La négation de la proposition
suivante "Pour tout x réel, il existe y réel tel que x<y" est :
a : "Il existe x
réel, tel que pour tout y réel , x supérieur ou égal à y ".
Vrai.
b : "Pour tout x réel, il existe y
réel tel que x >y". .
c : "Il existe x
réel , tel que pour tout y réel , x <y "
d : Aucune des 3
réponses précédentes n’est exacte.
7. Parmi les quatre
propositions suivantes, laquelle est vraie ?
a : "Il existe x
entier, tel que pour tout y réel , x<y"
b : "Pour tout x
réel, pour tout y réel, x2-y2 >0"
c : "Il existe x
réel, tel que pour tout y réel, xy=2"
d : "Pour tout x
réel, pour tout y réel, xy2 = yxy". Vrai.
8. Parmi les quatre
propositions suivantes, laquelle est fausse ?
a : "Pour tout x
réel, si x>0 alors 1/x >0".
b : "Pour tout e appartenant à ]0 ; +oo[,
il existe h appartenant
à ]0 ; +oo[, tel que pour tout x réel, si |x|< h alors |3x| < e
c : "Pour
tout e
appartenant à ]0 ; +oo[, il existe h appartenant
à ]0 ; +oo[, tel que pour tout x réel, si |x|< h alors |1/x| < e Vrai.
d : "Pour tout réel, s ix=0 alors
(x+)(x-1)x=0".
Représentation
graphique d'une fonction.
9. Quelle que soit
la fonction définie sur R, sa courbe représentative admet :
a : exactement une
droite asymptote horizontale
b : au maximum une
droite asymptote horizontale
c : au maximum deux
droites asymptotes horizontales. Vrai.
d: au minimum une
droite asymptote horizontale.
On considère une fonction définie sur R-{3}. La fonction est continue
sur son domaine de définition, elle est strictement monotone sur les
intervalles. Le tableau de variation de est le suivant :
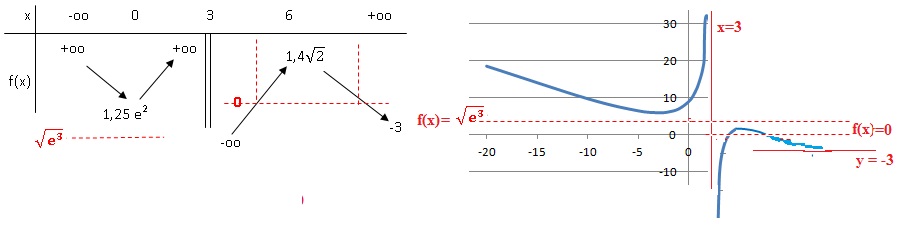
10.
La limite de f(x) quand x tend vers moins l'infini est :
a : 3.
b : +oo. Vrai.
c : -oo.
d: -3.
11. Dans le domaine
de définition de f, l’équation f(x)=0 admet :
a : aucune solution.
b : exactement 1
solution.
c : exactement 2
solutions. Vrai.
d : exactement 3
solutions.
12. La courbe
représentative de f(x) admet :
a : aucune droite
asymptote.
b : exactement 1
droite asymptote, horizontale ou verticale.
c : exactement 2
droites asymptotes, horizontales ou verticales. Vrai.
Droite d'équation x = 3 et droite d'équation y = -3
d : exactement 3
droites asymptotes, horizontales ou verticales.
13. Dans le domaine
de définition, l’équation f(x) = e3/2 admet :
a : aucune solution. Vrai.
b : exactement 1 solution.
c : exactement 2
solutions.
d : exactement 3
solutions.
e3/2 ~4,48 ; 1,25 e2
~9,1 >4,48, donc aucune solution dans ]-oo ; +3[.
1,4 x2½ ~1,98< 4,48, donc aucune solution dans ]3 ; +oo[.
14. On considère la
fonction définie par pour tout x réel par g(x) =f(x2+4).
Alors la limite de g(xpour x tendant vers l'infini est :
a : 3 ; b : +oo ; c : -oo ; d . -3. Vrai.
Quand x tend vers l'infini :
x2+4 tend vers l'infini ;
de plus f(x) tend vers l'infini.
Donc, f(x2+4) tend vers l'infini.
|
| .
. |
|
|
Equations.
15. Dans R le trinôme z2+6z+11=0 admet :
a :
deux racines réelles.
b : deux racines
complexes conjuguées.
c : aucune racine. Vrai.
d : une racine
réelle double.
Discriminant D = b2-4ac
= 36-4x11 = 36-44 = -9
Le discriminant étant négatif, ce trinôme n'admet aucune racine réelle.
16. On considère la
fonction f définie par f(x) = cos (x+p/3) sin(x-p/4) pour tout x réel. Alors
l'équation f '(x)=0 admet pour solutions dans [0
; p] :
a. 5p/24 et 17p/24. Vrai.
b. p/6
et p/4.
c.
-7p/24 et -19p/24.
d.
Aucune des 3 réponses précédentes n’est exacte.
On pose u = cos
(x+p/3) et v = sin(x-p/4); u' = -sin (x+p/3) ; v' = cos(x-p/4)
f '(x) = u'v +v' u = -sin (x+p/3)sin(x-p/4)+cos(x-p/4) cos
(x+p/3).
f '(x)=0,5 cos [(x-p/4)+(x+p/3)]=0,5 cos(2x+p/12).
f '(x) = 0 entraîne 2 x +p/12
=±p/2 +2kp ;
x =± p/4
-p/24
+kp ; x =5p/24
et x = 17p/24.
17.
Dans R l'équation admet e2x+ex+4 = ln((e-1) /17).
a. aucune solution.
Vrai.
b. exactement une
solution.
c. exactement deux
solutions.
d. exactement trois
solutions.
e2x+ex+4
est positif quel que soit x réel ; (e-1) /17 est inférieur à 1 ; ln((e-1) /17) est négatif.
18. Dans ]-p ; +p] l'équation sin(x) = ln
[exp(2x+3) / exp(2+2x) ] cos (x) admet :
a. aucune solution.
b. exactement une
solution.
c. exactement deux
solutions. Vrai.
d. exactement trois
solutions.
exp(2x+3)
/ exp(2+2x) = exp(2x+3-2x-2) = exp(1) = e ; ln(e) = 1.
sin(x) = cos(x) = sin ( p/2-x)
;
x = p/2-x +2kp et x =- p/2-x +2kp.
Fonction exponentielle.
19. On considère la fonction f
définie sur R par f(x)=(ex-2) / (ex+2), alors
pour tout x réel on a :
a. f '(x) = 2e2x
/(ex+2)2.
b.
f '(x) = (e2x -4)/(ex+2)2.
c.
f '(x) = 2ex /(ex+2)2.
d.
f '(x) = 4e2x /(ex+2)2. Vrai.
On pose u = ex-2 et v = ex+2 ; u' = v' = ex.
(u'v -v'u ) / v2=ex(ex+2 -ex+2) / (ex+2)2= 4ex
/ (ex+2)2.
20.
Quand x tend vers l'infini, la limite de x exp(1/x) est égale à :
a. 0 ; b. 1 ; c. -oo ; d. +oo. Vrai.
Quand x tend vers l'infini :
1/x tend vers zéro ; exp(1/x) tend vers 1 ; x exp(1/x) tend
vers + oo.
21.
Soient x et y deux nombres réels quelconques, on note A = exp((x+y)/2)
[exp((x-y)/2) +exp((y-x)/2)] et ,B = (exp(x) +exp(y) ) /e alors :
a. A=B ; b. A < B ; c. A >B Vrai ; c. On ne peut pas comparer A et B sans informations sur x et y.
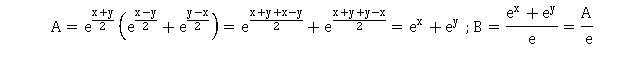 . .
22 . Quand x tend vers zéro, la limite de (e11x-e7x) / x est égale à : a. 0 ; b. +oo ; c. 4 Vrai ; d. 11 / 7.
e7x(e4x-1)/ x avec, au soisinage de zéro, e4x~1+4x.
(e4x-1) ~4x ; (e4x-1)/ x ~4 ; e7x ~1 ; e7x(e4x-1)/ x ~4.
Fonction logarithme népérien.
23. ln(16) +2 ln(3) -ln(24) est égal à :
a. 0 ; b. 2ln(3) ; c. ln(6) Vrai ; d. ln(5).
ln(16) +ln(9)-ln(24) = ln (16 x9 /24) = ln(6).
|
|
|
|
24. Pour tout x appartenant à ]-3 ; 3 [, ln(9-x2) est égal à :
a. 2ln(3)-ln(x).
b. ln(-3-x) +ln(-3+x).
c. ln(-3-x) ln(-3+x).
d. Aucune des 3 réponses précédentes n'est exacte. Vrai.
ln(9-x2)=ln[(3-x)(3+x)]= ln(3-x) +ln(x+3).
25. Quand x tend vers l'infini, la limite de 4x-3ln(x) est égale à :
a. 0 ; b. +oo Vrai ; c. -oo ; d. Aucune des 3 réponses précédentes n'est exacte.
Par croissance comparée, 4x croît plus vite que 3ln(x).
26. Quand x tend vers zéro, la limite de A est égale à :
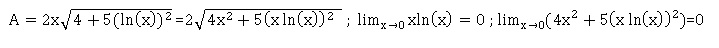
a. 0 Vrai; b. +oo ; c. -oo ; d. Aucune des 3 réponses précédentes n'est exacte.
27. On considère la fonction f définie sur ]0 ; +oo[ par f(x) = xlnx-x alors pour tout x de cet intervalle :
a. f '(x) = 1/x-1 ; b. f '(x) = ln(x)-2 ; c. f '(x) = 1-x ; d. f '(x) = ln(x). Vrai.
On pose u = x et v = ln(x) ; u'=1 ; v' = 1/x ; u'v+v'u=ln(x)+1 ; f '(x) = ln(x)+1-1 = ln(x).
28. On considère la fonction f définie sur R par f(x) =x3/(x4+2), alors une primitive de f est :
a. f(x) = ln(x4+2) ; b. f(x) = 4 ln(x4+2) ; c. F(x) = 0,25 ln(x4+2) Vrai ; d. F(x) =ln(x4+2) / 3.
On pose u = x4+2 ; u' = 4x3 ; f(x) = (u' / u) / 4 ; F(x) = ln(u) / 4.
|
|