Mathématiques, nombres complexes, géométrie dans l'espace,suites concours Avenir 2015

Mathématiques, nombres complexes, géométrie dans l'espace, suites, concours Avenir 2015

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

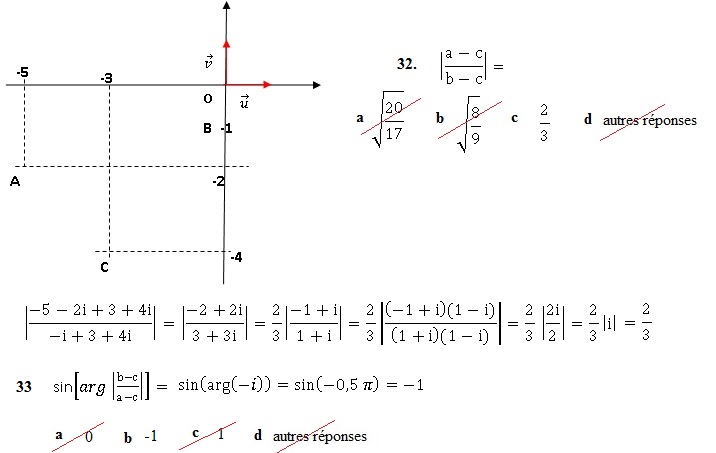
Géométrie plane et nombres complexes.
Soient les points A, B, C du plan complexe, d’affixes respectives a = −5−2i, b = −i et c = −3−4i

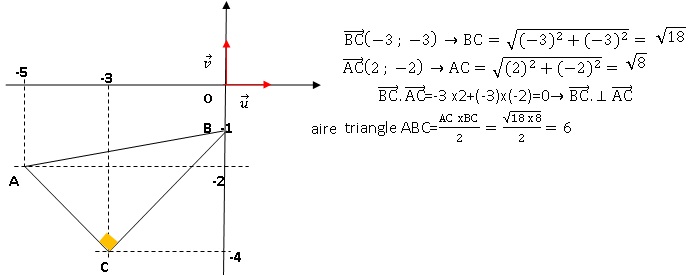
34. En unités d'aire, l'aire du triangle ABC est égale à
a. 2. b. 3. c. 6 Vrai .d. 12.

35. L’équation réduite de la droite (d) passant par C et parallèle à (AB) est
a. y=0,2x-17/5 Vrai; b. y=0,2x+17/5 ; c.y=5x+11 ; d. y=5x-11. Vrai.
La droite (AB) est dirigée suivant le vecteur de coordonnées (5 ; 1).
La droite (d) est dirigée suivant le vecteur de coordonnées (5 ; 1) et passe par C(-3 ; -4) :
Equation paramétrique de cette droite : x = 5t-3 ; y = t-4.
t = y+4 soit x = 5y+20-3 ; y = 0,2x-17/5.

36. L’équation réduite de la médiatrice du segment [CB] est :
a : y=x-1. . b :y= -x+1 . c : y=x+4. d : y=-x-4. Vrai.
La droite (BC) est dirigée suivant le vecteur de coordonnées (-3 ; -3).
La médiatrice au segment [BC] est dirigée suivant le vecteur de coordonnées (+1/3 ; +1 / 3)
Cette médiatrice passe par le point sde coordonnées : (0-3) / 2 ; (-4-1)/2 soit -1,5 ; -2,5.
Equation paramétrique de cette médiatrice : x = 1/3t-1,5 ; y = 1/3t-2,5.
1/3t= -x-1,5 ; y=-x-4
.
37. La parabole d’équation y = ax² +ßx +g passant par les points A, B et C est telle que :
a : ß >0 et g >0. b : ß >0 et g <0. . c : ß <0 et g >0. d : ß <0 et g <0.
La parabole passe par B(0 ; -1) : -1 = g.
La parabole passe par A(-5 ; -2) : -2 = 25a -5ß+g ; -2 = 25a -5ß-1 ; -1 = 25a -5ß ;
La parabole passe par C(-3 ; -4) : -4 = 9a -4ß+g ; -4 = 9a -4-1 ; -3 = 9a -4ß ;
-9=225a -45ß ; -75 = 225a -100ß ; soustraire : 66=55ß. ß = 6/5.

.
.

Algorithme.
On considère l’algorithme suivant :
Saisir un entier N inférieur ou égal à 4
Saisir un entier P supérieur ou égal à 6
Tant que N +1 est inférieur ou égal à P
Affecter à N la valeur N +1,5
Affecter à P la valeur P −N
Fin de Tant que
Si N est un entier alors afficher N
Sinon afficher P
Fin de Si
38. Pour N = 4 et P = 6, le nombre affiché est
a : 0,5 Vrai b : 2. c : 5,5. d : aucune des réponse précédentes. Vrai..

N
4
4+1,5=5,5

P
6
6-5,5=0,5

39.Pour N = 1 et P = 9, le nombre affiché est
a : 3 Vrai.. b : 3,5. c : 4. Vrai. d : aucune des réponses précédentes.

N
1
1+1,5=2,5
2,5+1,5=4

P
9
9-2=6,5
6,5-4=2,5

Géométrie dans l'espace.
Dans le repère orthonormé de l’espace, on considère les points A(1 ; 3 ; 2), B(−1 ; 3 ; 3), C(0 ; 3 ; −2), D(2 ; -2 ; 0) et E(8 ; −2 ; −3).
40.

41. Une équation paramétrique de la droite (BD) est
a. x = -6t+5 ; y = 10t-7 ; z = 6t-3. Vrai. b. x=-t+2 ; y =3t-2 ; z = 3t.
c : x=3t+1 ; y = -5t-3 ; z = -3t-3. d : aucune des réponse précédentes. Vrai.
La droite (DB) est dirigée suivant le vecteur de coordonnées [-1-2 ; 3 -(-2) ; 3-0) soit (-3 ; 5 ; 3).
De plus elle passe par le point B(-1 ; 3; 3).
Une représentation paramétrique de cette droite est : x = -3t-1 ; y = 5t+3 ; z = 3t+3, t réel.
Le point de coordonnées (5 ; -10 ; -3 ) appartient à cette droite, il suffit de prendre t = -2.

42. Une équation cartésienne du plan passant par D et perpendiculaire à (AB) est
a. -2x+z= -6.
b. 6x-3z =18.
c. 6y+5z =12
d. aucune des propositions précédentes. Vrai.
La droite (AB) est dirigée suivant le vecteur de coordonnées ( -1-1 ; 3-3 ; 3-2) soit (-2 ; 0 ; 1)
Equation cartésienne de ce plan : -2x +z = a.
Le point D(2 ; -2 ; 0) appartient à ce plan : -2 x2 +0 = a ; a = -4.

43. Le nombre de plans parallèles à (AB) passant par les points D et E est
a. 0 ; b. 1 ; c. 2 .; d. infini. Vrai

44. Une équation cartésienne du plan passant par les points A et C et parallèle à (BD) est
a. x-y+z=0; b. 4x+2y-z=8 ; c. 2x+3y-3z=5; c. aucune des propositions précédentes. Vrai.
Une représentation paramétrique de la droite (BD) est : x = -3t-1 ; y = 5t+3 ; z = 3t+3, t réel.
Cette droite est dirigée suivant le vecteur de coordonnées (-3 ; 5 ; 3).

45 . Le triangle BCD est : a. rectangle, non isocèle ; b.rectangle isocèle ; c. isocèle non rectangle ; d. aucune des propositions précédentes.Vrai.

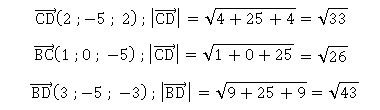
Les côtés ont des mesures différentes et la relation de Pythagore n'est pas vérifiée..

Suites d'intégrales.
Soient (A_n) et (B_n) les suites définies pour n supérieur ou égal à 1 par :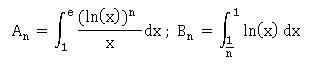
50. (B_n) est :
a. constante ; b. strictement décroissante. Vrai c. strictement croissante. d.non monotone.
Primitive de ln(x) :F= x (ln(x)-1) ; F(1) = -1 ; F(1/n) = -1/n (ln(n)+1) ; B_n = -1+1/n (ln(n)+1).

51 Pour tout n supérieur ou égal à 2, (B_n) est :
a. strictement négatif Vrai ; b. strictement pôsitif ; c. nul ; d. Aucune des 3 réponses précédentes n'est exacte.

52. A₁=
a. 1/4 ; b. 1/3 ; c. 1/2, Vrai ; d. 1.
Primitive de ln(x) / x ; on pose u = ln(x) ; u' = 1/x ; primitive de u u' = ½u² soit 0,5 (ln(x))².
A₁ = 0,5 (ln(e))²-(ln(1))²=0,5 x1-0=0,5.

53. A₂=
a.1/4 ; b. 1/3 Vrai ; c. 1/2 ; d. 1.
On pose U = ln(x) ; U' = 1/x ; (ln(x)² / x =U²U' ; primitive de U²U' =U³ / 3 =( ln(x))³ / 3.
A₂ =( ln(e))³ / 3 -( ln(1))³ / 3 = 1/3-0=1/3.

54. (A_n) est :
a. constante ; b. strictement décroissante Vrai ; c. strictement croissante ; d. non monotone.

55. (A_n)
a. converge Vrai ; b. diverge vers -oo ; c. diverge vers +oo ; d. diverge sans limite.

.

menu