Mathématiques, concours Avenir 2014

Mathématiques, concours Avenir 2014

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

On lance deux fois de suite et de manière indépendante un dé parfaitement équilibré à six faces dont : deux sont blanches marquées chacune du chiffre 2 ; une est blanche marquée du chiffre 1 ; une est noire marquée du chiffre 1 et les deux autres sont noires marquées du chiffre 3. On considère les variables aléatoires X correspondant à la somme des deux chiffres obtenus et Y le nombre de couleurs différentes obtenues.

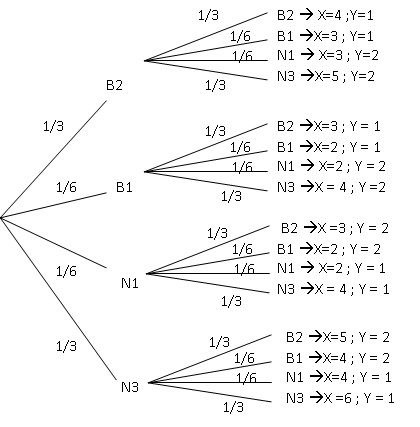
33. Le nombre de valeurs différentes pouvant être prises par X est :
a.3. b. 4. c. 5. Vrai. d. 6.
X peut prendre les valeurs 2, 3, 4, 5 et 6.

34.P(X=2)= :
a.1 / 6
b. 2 / 36.
c.4 / 36. Vrai.
d. aucune des trois propositions ci-dessus n'est correcte.
Probabilité d'obtenir une face marquée 1 : 2 / 6.
P(X=2) = 2 / 6 x 2 / 6 = 4 /36

35. P(Y=1)-P(Y=2) est :
a. nul. vrai : b. strictement négatif : c. strictement positif. d. aucune des valeurs précédentes.
Probabilité d'obtenir deux fois un blanc : 0,5 x0,5 = 0,25.
Probabilité d'obtenir deux fois un noir : 0,5 x0,5 = 0,25.
P(Y=1 )= 0,5.
Probabilité d'obtenir un blanc et un noir P(Y=2) = 0,5.

36. P(X=Y) = :
a : P(X=1). b : P(X=2). c : P(X=1) +P(X)=2). d : aucune des trois propositions ci-dessus n'est correcte. Vrai.
X = 2 ; Y =2. P(X=Y) = 1 / 36 +1 / 36 = 1 / 18.

37. L'espérance mathématique est E(Y) = :
a : 0,5. b : 2 . c :1,5. Vrai. d : 2.
1 (2 /9 +4 /18 +2 /36 )+2( 4/18 +2 /9 +2 /36)=0,5 +2 x0,5=1,5.

38.P_Y=2(X=2)= :
a. 0,5 ; b. 1 /9, vrai ; c. 1/18.
d : aucune des trois propositions ci-dessus n'est correcte.
P(X=Y=2) / P(Y=2) = (1 /18 ) /0,5= 1 /9.

39. P_X=2(Y=2)= :
a : 0,5. Vrai.
b : 1/9.
c :1/18.
d : aucune des trois propositions ci-dessus n'est correcte.
P(X=Y=2) / P(X=2) = (1 /18 ) / (4 /36)= 0,5.

Géométrie non analytique dans l'espace.

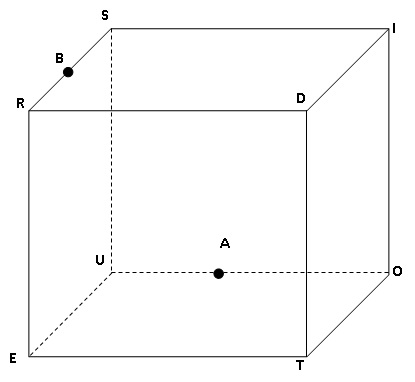
A milieu de [OU) et B milieu de [RS]
40. La section de ce cube par le plan (EAS) est :
a. un segment ; b. un triangle, Vrai ; c. un quadrilatère ;
d : aucune des trois propositions ci-dessus n'est correcte.
Cette section est le triangle EAS.

41. La section de ce cube par le plan (EAB) est :
a. un segment ; b. un triangle ; c. un quadrilatère, Vrai ;
d : aucune des trois propositions ci-dessus n'est correcte.
La section par le plan (EAB) est un quadrilatère ayant pour sommets EAB et un point sur l’arête SI.

.
.

42. La section de ce cube par le plan (EAD) est :
a. un segment ; b. un triangle ; c. un quadrilatère Vrai ;
d. aucune des trois propositions ci-dessus n’est correcte.
La section par le plan (EAD) est un quadrilatère de sommets EAD et un point de l’arête IO.

Géométrie analytique dans l'espace.
Dans le repère orthonormé de l’espace, on considère les points A(0 ; −5 ; 0), B(1 ; 0 ; 1),
C(−1 ; −7 ; 0), la droite D d’équation paramétrique :
x = −6a +6
y = 4a −9
z = 0
où a appartient à R et le plan P d’équation cartésienne : 3x −2y −10 = 0.
43. Le point A :
a : appartient à D et à P. Vrai. b : appartient à D mais pas à P . c : appartient à P mais pas à D. d : n'appartient ni à D ni à P.
3x_A −2y_A −10 = 0-2(-5)-10 =0 ; A appartient à P..
x_A = −6a +6=0 soit a = 1
y_A = 4a −9=-5 soit a = 1
z = 0. Le point A appartient à D.

44. Le triangle ABC est :
a : rectangle en A. b : rectangle en B. c :-rectangle en C. d : aucune des réponse précédentes. Vrai.

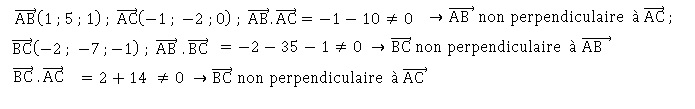
45. D et P sont :
a. parallèles b. sécants non perpendiculaires. c : perpendiculaires. Vrai. d : aucune des réponse précédentes.

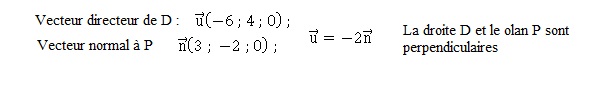
46. Les droites (AD) et D sont :
a. parallèles. b. sécantes non perpendiculaires. Vrai. c. perpendiculaires. d. aucune des solutions précédentes.

47. C est sur la sphère de centre B et de rayon r où r appartient à l’intervalle :
a. [5 ; 6] ; b. [6 ; 7 ] ; c. [7 ; 8] vraii ; d. [8 ; 9]..
R²=BC² = (-2)² +(-7)²+(-1)² =54. R = 54^½.

Algorithmique. On considère l’algorithme suivant :
Saisir un entier N >1
Affecter à S la valeur 1
Affecter à T la valeur 1
Tant que T < N
Affecter à S la valeur S +ln(T )
Affecter à T la valeur T +1
Fin de tant que
Affecter à L la valeur S −1
Afficher L
48. La valeur de L affichée pour N = 1 est ::
a. 0 vrai ; b. 1. c. 2 ; d. aucune des propositions précédentes.
S = 1 + ln 1 = 1 ; L = S-1 = 0.
49 . La valeur de L affichée pour N = 3 est :
a. ln(5) ; b. ln(6), vrai . c. ln(7) ;
d. aucune des propositions précédentes.

S
1
1+ln(1)=1
1+ln(2)
1+ln(2) +ln(3)

T
1
2
3
4

L = ln(2) +ln(3) = ln (6).

50. La plus grande valeur de N telle que L <ln(25) est :
a. 3 ; b. 4, vrai . c.5;
d. aucune des propositions précédentes.

N

1
2
3
4
5

S
1
1+ln(1)=1
1+ln(2)
1+ln(2) +ln(3)=1+ln(6)
1+ln(6) +ln(4)=1+ln(24)
1+ln(24)+ln(5)=1+ln(120)

T
1
2
3
4
5
6

L

0
ln(2)
ln(6)
ln(24)
ln(120)

51. La plus petite valeur de N telle que e^L >25 est :
a. 3 ; b. 4, . c. 5; vrai
d. aucune des propositions précédentes.
L > ln(25).

Lois de densité.
X suit la loi normale de moyenne −2 et de variance V telle que P(X < 0) = a et Y suit la loi exponentielle de paramètre 0,2.
52. Ainsi :
a.0,5 ; b. < 0,5. c. a > 0,5. Vrai.
d. Aucune des 3 réponses précédentes n'est exacte.
P(X<0) >P(X =-2)=0,5.

53. P(X=0) = :
a. 0 vrai; b. 0,5 ; c. 1; d. Aucune des 3 réponses précédentes n'est exacte.
P(X=0) = P(X=a), quelque soit a.

54. P(-2 <X <0)= :
a. a-0,5 vrai ; b. a+0,5; c. 2 ; d. aucune des proposition proposée.
P(X<0) -P(X<-2) = a-0,5.

55. P(X<-2) = b où :
a. b=0,5 vrai; b. b <0,5 ; c. b >0,5 ; d. aucune des proposition proposée.
(-2+1) / 2= -0,5.

56. E(Y) = :
a. 0,2; b. 5, vrai ; c. 5 ln(2) ;
d. Aucune des trois propositions proposées n'est correcte.
E(Y) = 1 / 0,2 = 5.

57. P(-1 < Y < 1)= :
a. e^0,2-e^-0,2 ; b. e^-0,2-e^0,2; c. 1-e^0,2 ; d. 1-e^-0,2. Vrai.
P(-1 < Y < 1)= P(Y<1)=1-e^-0,2.

58. La valeur de q telle que P(Y < q) = P(Y > q) est :
a. 0 ; b. 0,5 ; c. 1 ; d. aucune des propositions précédentes.
1-e^-0,2q =e^-0,2q ; e^-0,2q= 0,5 ; -0,2q=ln(0,5) = -ln(2) ; q=5ln2. Vrai.

59. P_Y>8(Y<5) :
a. ( P(Y<8) -P(Y<5) ) / P(Y<8) ; b. ( P(Y>8) -P(Y<5) ) / P(Y>8) ; c. 1-P(Y<3) ; d. aucune des propositions précédentes. vrai
Y ne peut pas être à la fois supérieur à 8 et inférieur à 5.

60. P_Y<8(Y<5) :
a. ( P(Y<8) -P(Y<5) ) / P(Y<8) vrai; b. ( P(Y>8) -P(Y<5) ) / P(Y>8) ; c. 1-P(Y<3) ; d. aucune des propositions précédentes.

.

menu