Mathématiques,
concours Avenir 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
Algorithmique.
On considère l'algorithme suivant :
Saisir un entir N supérieur ou égal à 1
Affecter à S la valeur 0
Affecter à I la valeur 0
Tant que S < N
Affecter à S la valeur S+I2
Affecter à I la valeur I+1
Fin de tant que
Afficher S
Afficher I.
34. La valeur de S affichée pour N=30 est :
a.14.
b. 30. Vrai.
c. 35.
d.
aucune des trois propositions ci-dessus n'est correcte.
S
|
0
|
1
|
1+4=5
|
5+9=14
|
14+16=30
|
I
|
1
|
2
|
3
|
4
|
5
|
35. La valeur de I affichée pour N=30 est :
a. 4 : b. 5 vrai : c. 6. d. aucune des valeurs précédentes.
36. La plus petite valeur de N telle que I = 3 est :
a : 1. b : 2 . vrai. c : 3. d : aucune
des trois propositions ci-dessus n'est correcte.
Pour N = 1 : S=1 et I = 2 ; pour N=2 : S=5 et I = 3.
37. La plus grande valeur de N telle que I = 3 est :
a : 1. b : 3 . c : 5 vrai. d : aucune
des trois propositions ci-dessus n'est correcte.
Pour N = 1 : S=1 et I = 2 ; pour N=2 : S=5 et I = 3.
Pour N = 4 : S= 5 et I=3 ; pour N = 5 : S=5 et I = 3 ; pour N = 6 : S=14 et I=4.
Les complexes.
38. l'écriture exponentielle de 3½-i est :
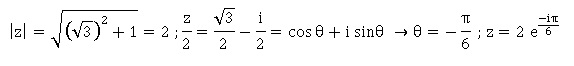
Réponse c.
39. (3½-i)9 est :
a : un réel strictement négatif.
b : un réel strictement positif.
c :un imaginaire pur. Vrai.
d :
aucune des
trois propositions ci-dessus n'est correcte.
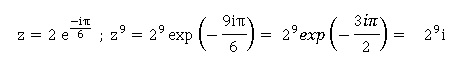
Dans
un repère orthonormé direct du plan complexe, on considère
l'application f qui a tout point M d'affixe z différent de -2 associe
le point M' d'affixe z' = (z-1) / (z+2)
40. Si z = -i alors z' = :
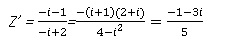
Réponse a.
41. Si z' = -i alors z = :
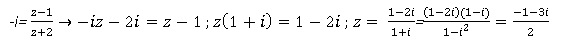
Réponse b.
|
| .
. |
|
|
42. L'ensemble des points M tels que OM' = 1 est :
a : une droite privée d'un point. b : un cercle privé d'un point . c
:une droite. vrai. d : un cercle
|z'|=1 =|z-1| / |z+2| avec z = x +iy x et y réels.
|x+2+iy| = |x-1+iy| ; (x+2)2 +y2 = (x-1)2 +y2 ;
(x+2)2 =( x-1)2 ; x+2 = ±(x-1) ; x = -½.
z doit être différent de -2 soit (-2)2 différent de (-0,5)2 +y2.
4 différent de 0,25 +y2 ; y2 différent de 3,75 ; y différent de ±15½ / 2.
43. l'ensemble des points M tels que est z' soit égal à l'opposé de son conjugué est:
a : une droite privée d'un point. b : un cercle privé d'un point . c
:une droite. vrai. d : un cercle
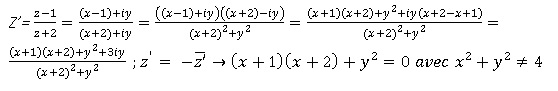
Réponse b.
Géométrie analytique dans l'espace.
Dans le repère orthonormé de l'espace, on considère les points A(0 ; -5
; 0), B(1 ; 0 ; 1), C( -1 ; -7 ; 0) et D(a ; 0 ; -1) où a est un réel.
44. Une équation du plan ( ABC) est
:
a : 3x+y+2z+5=0. b :
x+y-6z+5=0. c :-2x+y-3z+5=0. Vrai. d : aucune des réponse précédentes.
A appartient à ce plan : 3x0 +(-5) +2x0 +5 = 0 est vérifié.
B appartient à ce plan : 3x1 +0 +2x1 +5 = 0 n'est pas vérifié. (a) est faux.
A appartient à ce plan : 0 +(-5) -6x0 +5 = 0 est vérifié.
B appartient à ce plan : 1 +0 -6x1 +5 = 0 est vérifié.
C appartient à ce plan : -1-7-6x0+5 =0 n'est pas vérifié. ( b) est faux.
A appartient à ce plan : -2x0 +(-5) -3x0 +5 = 0 est vérifié.
B appartient à ce plan : -2x1 +0 -3x1 +5 = 0 est vérifié.
C appartient à ce plan : -2x(-1)-7-3x0+5 =0 est vérifié. ( c) est vrai.
45. Le triangle ABD est rectangle en B lorsque a =
a. 1. b. 3. Vrai. c : 4. d : aucune des réponse précédentes.
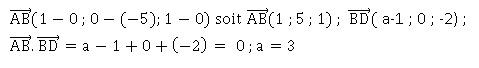
46.
Les droites (AD) et BC) sont parallèles lorsque a = :
a. -10 / 7. b. 10 / 7.
c. 4.
d. aucune des
solutions précédentes. Vrai.
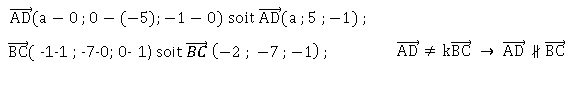
47. Le nombre de valeurs de a tel que AD=BC est : :
a. 0 ; b. 1 ; c. 2 vrai ; d.
aucune des réponses précédentes.
AD2 = a2 +52+(-1)2 =a2 +26 ; BC2 = (-2)2 +(-7)2 +(-1)2 = 54.
AD2 =BC2 ; a2 +26 =54 ; a2 = 28 ; a = ±28½.
48. x2-4x+y2+3y=4 est une équation :
a. de cercle Vrai ; b. de sphère. c. de plan ; d. aucune des propositions
précédentes. Vrai.
(x-2))2 +(y+1,5)2 -4-2,25=4 ; (x-2))2 +(y+1,5)2 =10,25 ; équation d'un cylindre d'axe Oz.
49 . Une équation de la sphère de centre C et de rayon OA est :
a. x2+2x+y2+14y+z2 = -25 vrai ; b. x2+2x+y2+14y+z2 = 25
.
c. x2-2x+y2-14y+z2 = -25 ;
d.
aucune des propositions précédentes.
(x-xC)2 +(y-yC)2+(z-zC)2 = (OA)2 ;
(x+1)2 +(y+7)2+z2 = (-5)2 ;
x2+2x+1+y2+14y+49+z2=25.
Les probabilités.
Soient deux événement A et B non impossibles, non certains et indépendants l'un de l'autre.
De manière générale :
50. 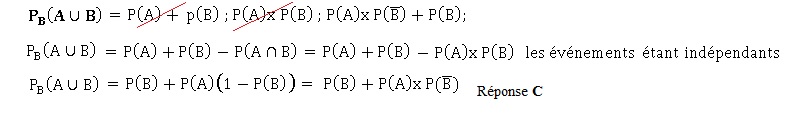 . .
51.

|
|
|
|
Soit
X une variable aléatoire qui suit la loi binomiale de paramètre (8 ;
0,3) ; Y suit une loi aléatoire qui suit une loi uniforme sur [-2 ; 1)
et Z est une varaible aléatoire qui suit la loi normale centrée réduite.
52. P(X=1)-P(X=7) est :
a. nul ; b. srictement négatif.
c. strictement positif. Vrai.
d. Aucune des 3
réponses précédentes n'est exacte.
P(X=1)=C81 x0,3 x0,77 = 8 x0,3 x0,77 ~0,1976.
P(X=7)=C87 x0,37 x0,7 = 8 x0,37 x0,7 =0,00122.
53. E(X)= :
a. 7,7 ; b. 8,3 ; c. 2,4 vrai; d. Aucune des 3
réponses précédentes n'est exacte.
8 x0,3 =2,4.
54. P(-1 <Y <2)= :
a. 1; b. 2/3 vrai ; c. -1 ; d. aucune des
proposition proposée.
Y suit une loi uniforme sur [-2 ; 1]: P(-1 <=Y <=2)= P(-1 <=Y <=1)=(1-(-1)) / (1-(-2))= 2 / 3.
55. E(Y) =
a. -1/3; b. 1 ; c. 1/3 ; d. aucune des
proposition proposée. Vrai.
(-2+1) / 2= -0,5.
56. P(Z< -2)- P(Z > 2) :
a.est nul, vrai ; b. est strictement négatif ; c. eqt strictement positif ;
d. Aucune des trois
propositions proposées n'est correcte.
57. E(Z) est :
a. nulle vrai ; b. strictement négative; c. strictement positive
; d. Aucune des trois
propositions proposées n'est correcte.
Les statistiques.
Mesdames Ave et Nir se présentent à une élection nationale.
Un sondage effectué sur un échantillon de n personnes (où n > 50) donne 52% des suffrages à Ave et 48 % à Nir. Soit p la proportion de votants pour madame Ave.
58. Pour n = 400, un intervalle de confiance de, au niveau de 95 % est :
a. [0,51 ; 0,53] ; b. [0,49 ; 0,55] ; c. [0,47 ; 0,57], vrai ; d. [0,47 ; 0,57]
1/ 400½ =0,05 ; [0,52 -0,05 ; 0,52 +0,05]
59. Le nombre minimal de personnes interrogées permettant d’affirmer, au niveau 95% que madame Ave va être élue est ::
a. 1500 ; b. 2000 ; c. 2500 vrai ; d. 3000.
0,52-n-½ doit être supérieur à 0,50 ; 0,02 >n-½ ; n > 1/0,022 ; n > 2500.
60. Pour
obtenir une amplitude 2 fois plus petite de l'intervalle de confiance
de p, il suffirait de multiplier le nombre initial de votants par :
a. 0,25 ; b. 0,5 ; c. 2 ; d. 4 vrai.
Amplitude = 2 / n½ ; en multipliant n par 4, l'amplitude est divisée par 2.
|
|