Etude de fonctions et de graphiques, brevet 2013

Etude de fonctions et de graphiques, brevet 2013.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

(sujet 2013)
Dans un jeu vidéo on a le choix entre trois personnages : un guerrier, un mage et un chasseur.
La force d’un personnage se mesure en points. Tous les personnages commencent au niveau 0 et le jeu s’arrête au niveau 25. Cependant ils n’évoluent pas de la même façon :
Le guerrier commence avec 50 points et ne gagne pas d’autre point au cours du jeu.
Le mage n’a aucun point au début mais gagne 3 points par niveau.
Le chasseur commence à 40 points et gagne 1 point par niveau.
Au début du jeu, quel est le personnage le plus fort ? Et quel est le moins fort ?
Le guerrier possède 50 points, c'est le plus fort. Le mage débute avec zéro point, c'est le plus faible.
Compléter le tableau suivant :

Niveau 0 1 5 10 15 25

Points du guerrier 50 50 50 50 50 50

Points du mage 0 3 15 30 45 75

Points du chasseur 40 41 45 50 55 65

À quel niveau le chasseur aura-t-il autant de points que le guerrier ?
Au niveau 10 le chaaseur et le guerrier ont le même nombre de points.
Dans cette question, x désigne le niveau de jeu d’un personnage.
Associer chacune des expressions suivantes à l’un des trois personnages : chasseur, mage ou guerrier :
Mage : f (x) = 3x ;
Guerrier : g (x) = 50 ;
Chasseur : h(x) = x +40.
Dans le repère suivant, la fonction g est représentée.
Tracer les deux droites représentant les fonctions f et h.
Déterminer à l’aide du graphique, le niveau à partir duquel le mage devient le plus fort.

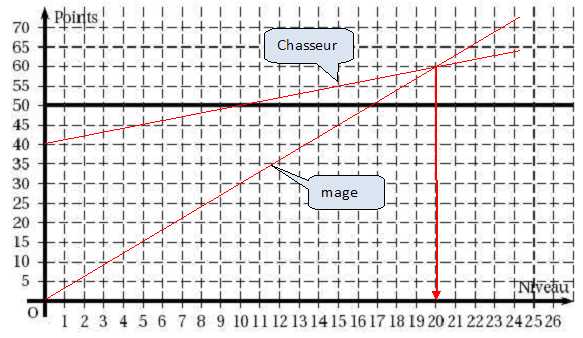
Le mage devient le plus fort à partir du niveau 20.

Dans cet exercice, on considère un rectangle ABCD tel que son périmètre soit égal à 31 cm.
Si un tel rectangle a pour longueur 10 cm, quelle est sa largeur ?
(31-2*10 ) /2 =5,5 cm.
Proposer une autre longueur et trouver la largeur correspondante.
L = 8 cm ; largeur : (31-2*8)/2 =7,5 cm.
On appelle x la longueur AB.
En utilisant le fait que le périmètre de ABCD est de 31 cm, exprimer la largeur BC en fonction de x.
BC =(31-2x) / 2 = 15,5-x.
En déduire l’aire du rectangle ABCD en fonction de x.
Longueur fois largeur = x(15,5-x) = 15,5 x-x².
On considère la fonction f définie par f (x) = x(15,5−x). Calculer f (4).
f(4) = 4(15,5-4) = 4*11,5 = 46 cm².
Vérifiez qu’un antécédent de 52,5 est 5.
52,5 = x(15,5-x) =5(15,5-5) =5*10,5 =52,5.
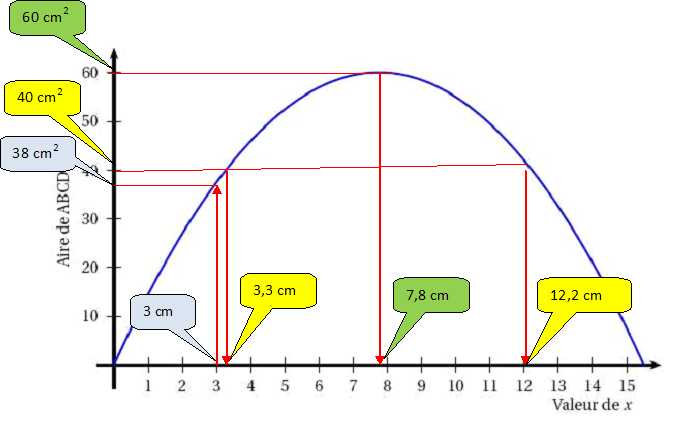
Sur le graphique ci-dessous, on a représenté l’aire du rectangle ABCD en fonction de la valeur de x.

.
.

À l’aide de ce graphique, répondre aux questions suivantes en donnant des valeurs approchées :
Quelle est l’aire du rectangle ABCD lorsque x vaut 3 cm ?
Pour quelles valeurs de x obtient-on une aire égale à 40 cm² ?
Quelle est l’aire maximale de ce rectangle ? Pour quelle valeur de x est-elle obtenue ?
Que peut-on dire du rectangle ABCD lorsqu’AB vaut 7,75 cm ? ABCD est un carré.

.

Lorsqu’on absorbe un médicament, la quantité de principe actif de ce médicament dans le sang évolue en fonction du temps.Cette quantité se mesure en milligrammes par litre de sang.
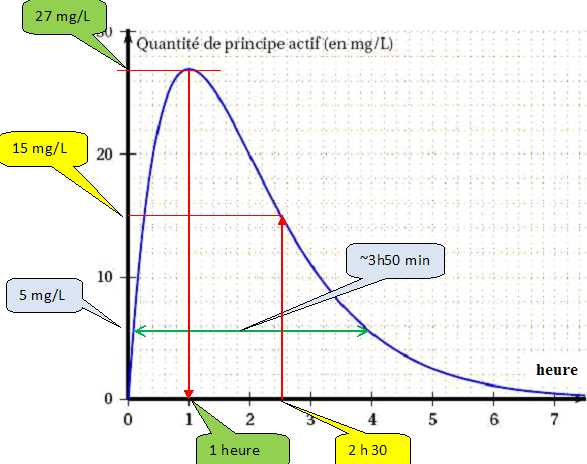
Le graphique ci-dessous représente la quantité de principe actif d’un médicament dans le sang, en fonction du temps écoulé, depuis la prise de ce médicament.
Au bout de combien de temps la quantité de principe actif de médicament dans le sang est-elle maximale ?
Quelle est la quantité de principe actif de médicament dans le sang au bout de 2 h 30 min?
Pour que le médicament soit efficace, la quantité de principe actif de médicament dans le sang doit être supérieure à 5 mg/L.
Pendant combien de temps le médicament est-il efficace ?

Comme cuve de récupération d’eau de pluie, Torres utilise un pavé droit dont les dimensions sont indiquées sur le schéma ci-dessous :

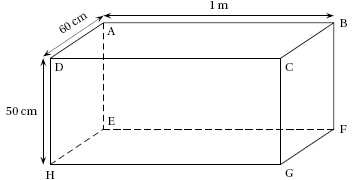
Montrer que le volume de la cuve est de 300 000 cm³. En déduire sa contenance en litres.
V = largeur fois longueur fois hauteur =60*50*100 =300 000 cm³ = 300 dm³ = 300 L.
Montrer que l’aire de la surface ABCD de récupération de l’eau de pluie est de 0,6 m².
Largeur fois longueur = 0,6*1 = 0,6 m².
En 2011 la quantité d'eau de pluie tombée à Poindimié est égale à 2550 mm.
On précise que 1 mm d’eau récupéré, c’est 1 litre d’eau lorsque la surface est 1 m².
Calculer le volume maximal x d’eau récupérée en 2011 par Torres.
0,6 *2550 =1530 L.
En 2011, Torres a récupéré 1 530 L d’eau de pluie.
Il faut en moyenne 1,5 L d’eau par semaine pour abreuver une poule.
Torres a-t-il eu suffisamment d’eau pour abreuver « gratuitement » ses 16 poules durant l’année 2011 ? Justifier.
Il y a 52 semaines dans une année.
Volume consommé : 16*1,5*52 =1248 L.
Combien de litres ne seront pas consommés ?
1530-1248=282 L
En se basant sur les résultats précédents, combien de poules supplémentaires pourrait-il abreuver ?
282 / (52*1,5) =3,6 soit 3 poules supplémentaires.

À partir du 2 Janvier 2012, une compagnie aérienne teste un nouveau vol entre Nantes et Toulouse. Ce vol s’effectue chaque jour à bord d’un avion qui peut transporter au maximum 190 passagers.
L’avion décolle chaque matin à 9 h 35 de Nantes et atterrit à 10 h 30 à Toulouse.
Calculer la durée du vol.
10 h30 -9 h 35 = 55 minutes.
Le tableau suivant donne le nombre de passagers qui ont emprunté ce vol pendant la première semaine de mise en service. L’information concernant le mercredi a été perdue.

Jour Lundi Mardi Mercredi jeudi Vendredi Samedi Dimanche Total

Nombre de passagers 152 143 145 164 189 157 163 1113

Combien de passagers ont emprunté ce vol le mercredi ?
1113-152-143-164-189-157-163 =145.
En moyenne, combien y avait-il de passagers par jour dans l'avion cette semaine là ?
1113 / 7 = 159.
À partir du mois de Février, on décide d’étudier la fréquentation de ce vol pendant douze semaines. La compagnie utilise une feuille de calcul indiquant le nombre de passagers par jour.
Cette feuille de calcul est donnée.

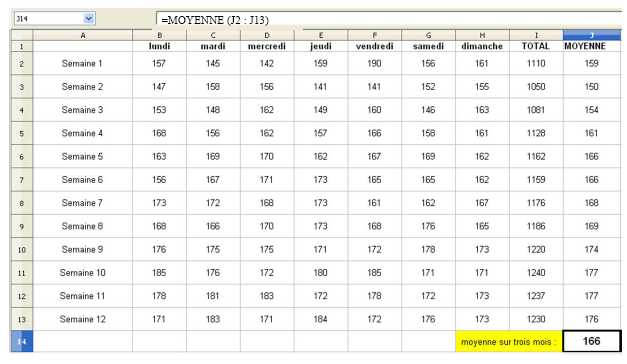
Quelle formule a-t-on saisie dans la cellule I2 pour obtenir le nombre total de passagers au cours de la semaine 1 ?
=SOMME(B2:H2).
Quelle formule a-t-on saisie dans la cellule J2 pour obtenir le nombre moyen de passagers par jours au cours de la semaine 1 ?
=MOYENNE(B2:H2) ou bien =I2/7.
Le nombre moyen de passagers par jour au cours de ces douze semaines est égal à 166. La compagnie s’était fixé comme objectif d’avoir un nombre moyen de passagers supérieur aux 80 %
de la capacité maximale de l’avion. L’objectif est-il atteint ?
190*0,80 =152 passagers, valeur inférieure à la fréquentation réelle : l'objectif est atteint.

Quand l’avion n’est plus très loin de l’aéroport de Toulouse, le radar de la tour de contrôle émet un signal bref en direction de l’avion. Le signal atteint l'avion et revient au radar 0,0003 secondes après
son émission. Sachant que le signal est émis à la vitesse de 300 000 kilomètres par seconde, vérifier qu’à cet instant, l’avion se trouve à 45 kilomètres du radar de la tour de contrôle.
Distance aller + retour =300 000*0,0003 =90 km ; distance aller ou retour 90 /2 = 45 km.
Le dessin n’est pas à l’échelle.

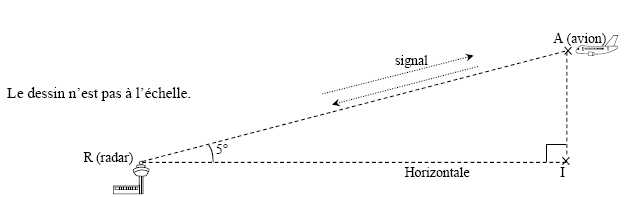
La direction radar–avion fait un angle de 5° avec l’horizontale. Calculer alors l’altitude de l’avion à cet instant. On arrondira à la centaine de mètres près.
On négligera la hauteur de la tour de contrôle. sin 5 = H / 45 ; H = 45 sin 5 =3,9 km.
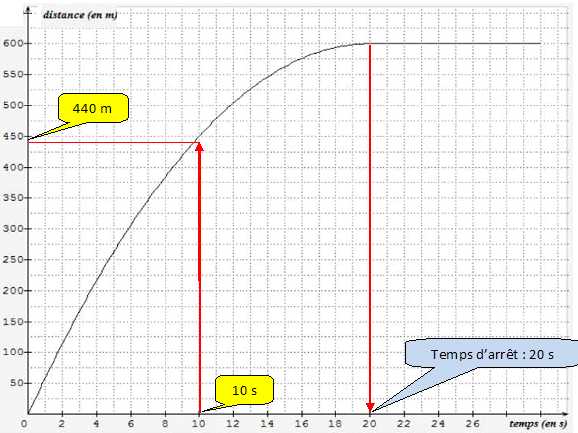
En phase d’atterrissage, à partir du moment où les roues touchent le sol, l’avion utilise ses freins jusqu’à l’arrêt complet. Le graphique suivant représente la distance parcourue par l’avion sur la piste (en mètres) en fonction du temps (en secondes) à partir du moment où les roues touchent le sol.
En utilisant ce graphique, répondre aux questions suivantes :
Quelle distance l’avion aura-t-il parcourue 10 s après avoir touché le sol ?
Expliquer pourquoi au bout de 22 s et au bout de 26 s la distance parcourue depuis le début de l'atterrissage est la même.
L'avion est à l'arrêt.
À partir du moment où les roues touchent le sol, combien de temps met l'avion pour s'arrêter ?

menu