Probabilités,
statistiques, tableur, brevet 2013.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
(sujet
2013)
Un restaurant propose cinq variétés de pizzas, voici leur carte :
CLASSIQUE : tomate, jambon, oeuf, champignons
MONTAGNARDE : crème, jambon, pomme de terre, champignons
LAGON : crème, crevettes, fromage
BROUSSARDE : crème, chorizo, champignons, salami
PLAGE : tomate, poivrons, chorizo.
Je
commande une pizza au hasard, quelle est la probabilité qu’il y ait des
champignons dedans ?
Nombre de pizzas contenant des champignons : 3
Nombre total de pizzas : 5.
Probabilité qu'il y ait des champignons :3/5 = 0,6.
J’ai
commandé une pizza à la crème, quelle est la probabilité d’avoir du
jambon?
Nombre de pizzas contenant de la crème : 3 ; nombre de pizzas contenant
de la crème et du jambon : 1.
Probabilité qu'une pizza à la crème contienne du jambon : 1/3 = 0,33.
Il est possible de commander une grande pizza composée à moitié d’une
variété et à moitié d’une autre. Quelle est
la probabilité d’avoir des champignons sur toute la pizza ?
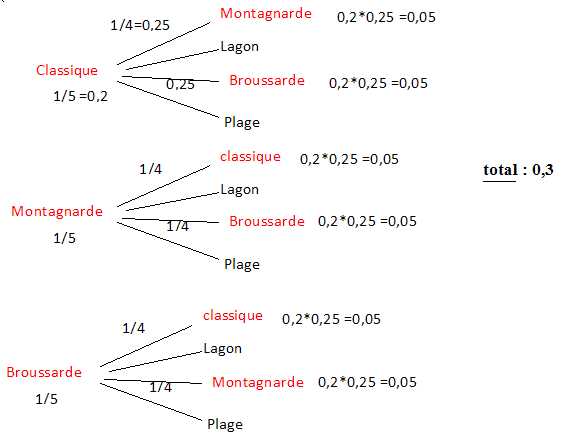
On pourra s’aider d’un arbre des possibles.
Probabilité d'aoir des champignons sur la première moitié : 3/5 = 0,6.
probabilité d'avoir des champignons sur la seconde moitié :2 / 4 = 0,5
Probabilité d'avoir des champignons sur toute la pizza : 0,6*0,5 = 0,3
 . .
On suppose que les pizzas sont de forme circulaire. La pizzeria propose
deux tailles :
moyenne : 30 cm de diamètre ; grande : 44 cm de diamètre.
Si
je commande deux pizzas moyennes, aurai-je plus à manger que si j’en
commande une grande ? Justifier la réponse.
On suppose que les pizzas grande et moyenne ont la même hauteur
Aire de deux pizzas moyennes : 2 pR2
=2*3,14*152 ~1414 cm2.
Aire d'une grande pizzas : pR2
=3,14*222 ~1520 cm2.
J'aurai le plus à manger en commandant une grande pizza.
|
.
.
|
|
|
L’épreuve
du concours
australien demathématiques est divisée en trois catégories :
• « Junior » qui regroupe les classes de 5e et 4e
• « Intermédiaire » pour les classes de 3e et 2nde
• « Senior » avec les classes de 1re et de
terminale.
Cette
année 25 établissements se sont inscrits. Plus de 3 000 élèves,
répartis comme l’indique le tableau suivant, ont participé à ce
concours.
Compléter
ce tableau . Les cases barrées ne sont pas à
remplir.
|
A |
B |
C |
D |
E |
F |
G |
| 1 |
Catégorie |
Juniors |
Intermédiaires |
Séniors |
| 2 |
effectifs
par catégorie |
|
1958 |
|
876 |
|
308 |
| 3 |
Niveau |
5e |
4e |
3e |
2nde |
1ere |
terminale |
| 4 |
effectif
par niveau |
989 |
969 |
638 |
238 |
172 |
136 |
| 5 |
Effectif total |
3142 |
638+238 = 876 ;
308-172 =136 ; 1958+876+308=3142.
Quel
est le niveau où il y a le plus d’inscrits ?
Il y a le plus d'inscrits en 5e.
Quelle
est la catégorie ayant le moins d’inscrits ?
Il y a le moins d'inscrits parmi les séniors.
En
moyenne, combien d’élèves par établissement ont participé
? Arrondir à l’unité.
3142/25 ~126.
Le tableau précédent est une copie d’écran d’un tableur.
Quelle
formule faut-il écrire dans la case G5 pour obtenir l’effectif total
?
= C2 + E2 + G2.
|
.
|
|
Le
salairemoyen brut des Français s’établissait en 2010 à 2 764 € par
mois. La population française est estimée en 2010 à 65 millions
d’habitants.
Encore un peu moins d’argent dans le porte-monnaie des
Français en 2010. Le salaire médian brut est celui qui partage la
population en deux parties égales, la moitié qui gagne plus, l’autre
moitié qui gagne moins ; il est égal à 1 610 € par mois.
Le niveau
de vie des français a baissé par rapport à 2009. D’ailleurs, le taux de
pauvreté enregistré en cette année 2010 est le plus haut jamais observé
depuis 1997. Il concerne 8,6 millions de Français qui vivent donc en
dessous du seuil de pauvreté évalué à 964 € par mois. »
Extrait
d’un reportage diffusé sur BFMTV en septembre 2012
En France, le salaire que touche effectivement un employé est égal au
salaire brut, diminué de 22% et est appelé le salaire net.
Montrer
que le salaire net moyen que percevait un français en 2010 était de 2
155,92 €.
2764 (1-0,22) =2764*0,78 =2155,92 €.
Expliquer
à quoi correspond le salaire médian brut.
La moitié des français gagne moins que le salaire médian ; l'autre
moitié gagne plus que le salaire médian.
Comparer
le salaire médian brut et le salaire moyen brut des Français.
Le salaire moyen brut est supérieur au salaire médian brut.
Salaire moyen brut / salaire médian brut = 2764/1610 ~1,72.
Comment
peut-on expliquer cette différence ?
Les salaires supérieurs au salaire moyen et perçus par un petit nombre
de personnes peuvent être très élevés.
Calculer
le pourcentage de français qui vivaient en 2010 sous le seuil de
pauvreté. On arrondira le résultat à l’unité.
8,6 / 65 ~0,13 ou 13 %.
Un
jeu1 est constitué des dix
étiquettes suivantes toutes identiques au toucher qui sont mélangées
dans un sac totalement opaque.
Deux angles droits seulement ;
Quatre angles droits ; Côtés égaux deux à deux ; Deux côtés
égaux
seulement ; Quatre côtés égaux ;
Côtés opposés parallèles ;
Deux côtés parallèles seulement ; Diagonales égales ;
Diagonales
qui se coupent en leur milieu ; Diagonales perpendiculaires.
On choisit au hasard une étiquette parmi les dix.
Quelle
est la probabilité de tirer l’étiquette «Diagonales égales »
?
Un cas favorable sur 10 étiquettes : la probabilité de tirer cette
étiquette est 1/10 = 0,10.
Quelle
est la probabilité de tirer une étiquette sur laquelle est inscrit le
mot « diagonales » ?
Trois étiquettes sur 10 portent le mot diagonales : la probabilité est
3/10 = 0,30.
Quelle
est la probabilité de tirer une étiquette qui porte à la fois le mot «
côtés »et le mot « diagonales » ?
Aucune étiquette ne porte les deux mots diagonales et côtés : la
probabilité est nulle.
On
choisit cette fois au hasard deux étiquettes parmi les dix et on doit
essayer de dessiner un quadrilatère qui a ces deux propriétés.
Madjid tire les deux étiquettes suivantes : Diagonales
perpendiculaires et Diagonales égales.
Julie affirme que la figure obtenue est toujours un carré. Madjid a des
doutes.
Qui a raison? Justifier la réponse.
Julie
a raison : dans un rectangle, les diagonales sont égales mais non
perpendiculaires ; dans un losange, les diagonales sont
perpendiculaires mais pas égales. dans un parallélogramme les
diagonales ne sont ni égales ni perpendiculaires.
Julie tire les deux étiquettes suivantes : Côtés opposés
parallèles Quatre côtés égaux.
Quel
type de figure Julie est-elle sûre d’obtenir ?
Le losange et le carré.
Lionel tire les deux étiquettes suivantes : Deux côtés égaux seulement
Quatre angles droits.
Lionel est déçu. Expliquer
pourquoi.
On ne peut pas construire de quadrilatère ayant 4 angles droits et
seulement deux côtés égaux.
D’après « Géométrie à l’Ecole »de François Boule. Savoir dire et
savoir-faire, IREM de Bourgogne.
|
Le
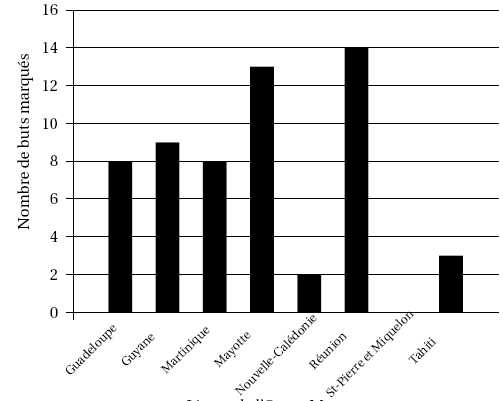
diagramme en bâtons ci-dessous nous renseigne sur le nombre de buts
marqués lors de la seconde édition de la coupe de l’Outre-Mer de
football en 2010.
Nombre de buts marqués par ligue.
Combien de
buts a marqué l’équipe deMayotte ?
Cette équipe a marqué 13 buts.
Quelle
est l’équipe qui a marqué le plus de buts ?
L'équipe de la Réunion a marqué le plus de buts.
Quelle(s)
équipe(s) ont marqué strictement moins de 8 buts ?
Les équipes de Nlle Calédonie, St Pierre et Miquelon, et Tahiti ont
marqué respectivement 2, 0 et 3 buts.
Quelle(s)
équipe(s) ont marqué au moins 10 buts ?
Les équipes de Mayotte et la Réunion ont marqué respectivement 13 et 14
buts.
Quel
est le nombre total de buts marqués lors de cette coupe de l’Outre-Mer
2010 ?
8+9+8+13+2+14+3=57 buts.
Calculer
la moyenne de buts marqués lors de cette coupe de l’Outre-Mer 2010.
57 / 8 ~7 buts.
Compléter
les cellules B2 à B10 dans le tableau ci-dessous.
|
A |
B |
| 1 |
Ligue
d'Outre Mer |
Nombre
de buts marqués |
| 2 |
Guadeloupe |
8 |
| 3 |
Guyane |
9 |
| 4 |
Martinique |
8 |
| 5 |
Mayotte |
13 |
| 6 |
Nlle
Calédonie |
2 |
| 7 |
Réunion |
14 |
| 8 |
Saint
Pierre et Miquelon |
0 |
| 9 |
Tahiti |
3 |
| 10 |
Total
: |
57 |
| 11 |
Moyenne
: |
7 |
Parmi
les propositions suivantes, entourer la formule que l’on doit écrire
dans la cellule B10 du tableau pour retrouver le résultat du nombre
total de buts marqués.
8+9+8+13+2+4+0+3 ; =Total(B2 : B9) ; =Somme (B2 : B9).
Écrire
dans la cellule B11 du tableau précédent une formule donnant la moyenne
des buts marqués.
=Moyenne
(B2:B9)
|
La
24e édition du Marathon International de Moorea
a eu lieu le 18 février 2012.
Des coureurs de différentes origines ont participé à ce marathon :
• 90 coureurs provenaient de Polynésie Française dont 16 étaient des
femmes.
• 7 coureurs provenaient de France Métropolitaine dont aucune femme,
• 6 provenaient d’Autriche dont 3 femmes,
• 2 provenaient du Japon dont aucune femme,
• 11 provenaient d’Italie dont 3 femmes,
• 2 provenaient des Etats-Unis dont aucune femme
• Un coureur homme était Allemand.
Compléter
le tableau ci-dessous à l’aide des données de l’énoncé.
|
Polynésie
française |
Métropole |
Autriche |
Japon |
Italie |
USA |
Allemagne |
| femme |
16 |
0 |
3 |
0 |
3 |
0 |
0 |
Combien de
coureurs ont participé à ce marathon ?
90 +7 +6+2+11+2+1=119.
Parmi les participants à ce marathon, quel
pourcentage les femmes polynésiennes représentent-elles ?
Arrondir au dixième près.
16 / (16+3+3) ~0,73 ou 73 %
À la fin du marathon, on interroge un coureur au hasard.
Quelle
est la probabilité que ce coureur soit une femme Autrichienne
?
3 femmes autrichiennes sur 119 participants : 3 / 119 ~0,025.
Quelle
est la probabilité que ce coureur soit une femme ?
22 femmes sur 119 participants : 22 / 119 ~0,18.
Quelle
est la probabilité que ce coureur soit un homme Polynésien
?
90-16 =74 hommes sur 119 participants : 74 / 119 ~0,62.
Quelle
est la probabilité que ce coureur ne soit pas Japonais ?
1-2 / 119 ~0,98.
Vaitea
dit que la probabilité d’interroger un coureur homme Polynésien est
exactement trois fois plus grande que celle d’interroger un coureur
homme non Polynésien.
A-t-il
raison? Expliquer pourquoi.
Probabilité d'interroger un homme non polynésien : 119-22 =97 hommes
dont 74 polynésiens.
Probabilité d'interroger un homme non polynésien : (97-74) / 119 = 23 /
119.
Probabilité
d'interroger un homme polynésien : 74 / 119.
Il a tord : 23 *3 = 69 diffère de 74.
Tom lance cinquante fois deux dés à six faces parfaitement équilibrés.
Il note dans une feuille de calcul les sommes obtenues à chaque lancer.
Il obtient le tableau suivant :
| B3 |
=B2/M2 |
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
| 1 |
somme obtenue |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
total |
|
| 2 |
nombre
d'apparitions |
3 |
1 |
4 |
6 |
9 |
9 |
7 |
3 |
5 |
3 |
0 |
50 |
|
| 3 |
fréquence
d'apparition |
0,06 |
|
|
|
|
|
|
|
|
|
|
|
|
Quelle
formule a-t-il saisie dans la cellule M2 pour vérifier qu’il a bien
relevé 50 résultats ?
=SOMME(B3:L3)
Tom a saisi dans la cellule B3 la formule =B2/M2 . Il obtient un
message d’erreur quand il la tire dans la cellule C3. Pourquoi
?
N3 ne contient rien, c'est à dire zéro ; en tirant dans la
cellule C3, cela conduit à une division par zéro.
Il aurait fallu saisir dans la cellule B3 : = B2 /$M$2.
Tom déduit de la lecture de ce tableau que s’il lance ces deux dés, il
n’a aucune chance d’obtenir la somme 12. A-t-il
tort ou raison ?
Il a tord, la fréquence d'apparition du nombre 6 est égale à 1/6.
:
|
 .
.