Calculs
d'aires et volumes, mise en équation, PGCD, brevet 2013.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
(sujet
2013)
Un enfant a ramassé 20 coquillages. Les grands mesurent 2 cm de long,
les petits mesurent 1 cm.
Tous les coquillages mis bout à bout font 32 cm au total.
Combien
a-t-il de grands coquillages et combien de petits ?
On
note x le nombre de petits
coquillages et 20-x le nombre de grands coquillages.
Longueur = 32 = x+2(20-x) ; 32 = x+40-2x ; x =8.
8 petits coquillages et 12 grands coquillages.
Un
vendeur de bain moussant souhaite faire des coffrets pour les fêtes de
fin d’année. En plus du traditionnel « pavémoussant », il veut
positionner par dessus une « pyramide moussante » qui ait le même
volume que le pavé.
Les schémas suivants donnent les dimensions (h désigne la hauteur de la
pyramide)
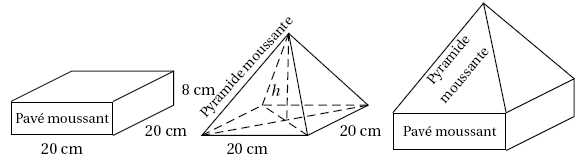 : :
On rappelle les formules suivantes :
Vpavé =
Longueur×largeur×hauteur
Vpyramide =aire de la base×hauteur /3
Calculer le volume d’un « pavé moussant ».
Vpavé
= Longueur×largeur×hauteur =20*20*8 =3200 =3,2
103 cm3.
Montrer
que le volume d’une « pyramide moussante » est égal à 400h/3
cm3. En
déduire la hauteur.
La
pyramide a le même volume que le pavé ; l'aire de la base de la
pyramide est égale à : 20*20 = 400 cm2.
3200 = 400 *h /3 ; 8 = h/3 ; h = 8*3 = 24 cm.
Un
pâtissier a préparé 840 financiers* et 1 176 macarons*. Il souhaite
faire des lots, tous identiques, en mélangeant financiers et macarons.
Il veut utiliser tous les financiers et tous les macarons. *
Les financiers et les macarons sont des pâtisseries.
Sans
faire de calcul, expliquer pourquoi les nombres 840 et 1 176 ne sont
pas premiers entre eux.
Ce sont des nombres pairs : ils admettent 2 comme diviseuur commun.
Le
pâtissier peut-il faire 21 lots ? Si oui, calculer le nombre de
financiers et le nombre de macarons dans chaque lot.
840 / 21 =40 ; 1176/21=56.
Il peutt faire 21 lots comptant chacun 40 financiers et 56 macarons.
Quel
est le nombre maximum de lots qu’il peut faire ? Quelle sera alors la
composition de chacun des lots ?
Rechercher le PGCD de 840 et 1176 :
840 = 40*21 = 8*5*3*7 =2 3*3*5*7 ; 1176 = 21*56 =
3*7*8*7 = 23*3*72.
PGCD(840 ; 1176 )=
23*3*7
=168.
840 / 168 =5 ; 1176 / 168 = 7.
Il peut faire au maximum 168 lots comptant chacun 5 financiers et 7
macarons.
Cette année, chaque lot de 5 financiers et 7
macarons est vendu 22,40 €. L’année dernière, les lots, composés de 8
financiers et de 14 macarons étaient vendus 42 €.
Sachant
qu’aucun prix n’a changé entre les deux années, calculer le prix d’un
financier et d’un macaron.
On appelle x le prix d'un financier et y le prix d'un macaron.
5x +7y = 22,4 ; 8x +14y = 42.
10x
+14y = 44,8 (1) ; 8x +14y = 42.
Soustraire (1)-(2) : 2x =2,8 ; x = 1,4 € ; y = (22,4-5*1,4) / 7 =2,2 €.
|
| .
. |
|
|
Le fleuve Amazone est celui qui
possède le débit moyen le plus important au monde. Il est d’environ 190
000 m3/s.
En France, un foyer de 3 personnes consomme en moyenne 10 000 L d’eau
par mois.
Donner
un ordre de grandeur du nombre de ces foyers que pourrait alimenter ce
fleuve en un an.
Rappel : 1 L = 1 dm3 et 1 m3
= 1 000 L.
Trois personnes consomment en moyenne
10 m3 par mois soit 120 m3
par an.
Volume d'eau débité par le fleuve en un an : 190
000*3600*24*365 ~ 1012 m3.
Nombre de foyers :1012
/120 ~ 5 1010.
|
.
|
|
Heiata
et Hiro ont choisi comme gâteau de mariage une pièce montée composée de
3 gâteaux cylindriques superposés, tous centrés sur l’axe (d) comme
l’indique la figure ci-dessous :
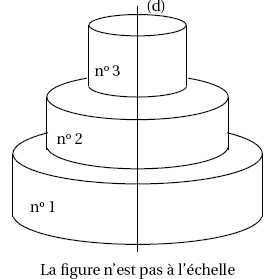
Les
trois gâteaux cylindriques sont de même hauteur : 10 cm. Le
plus grand gâteau cylindrique, le n° 1, a pour rayon 30 cm.
Le rayon du gâteau n° 2 est égal au 2 /3 de celui du gâteau n° 1. Le
rayon du gâteau n° 3 est égal au 3 /4 de celui du gâteau n° 2.
Montrer
que le rayon du gâteau n° 2 est de 20 cm.
30 *2 / 3 = 10*2 = 20 cm.
Calculer
le rayon du gâteau n° 3.
20*3 /4 = 5*3 = 15 cm.
Montrer
que le volume total exact de la pièce montée est égal à 15
250 p cm3.
Rappel : le volume V d’un cylindre de rayon R et de hauteur h est donné
par la formule V = p×R2
×h.
V = p×302
×10 +p×202
×10 +p×152
×10 = 10 p(302 +202 +152)
=10 p(900 +400
+225) =15 250 p cm3.
Quelle
fraction du volume total représente le volume du gâteau n° 2 ? Donner
le résultat sous forme de fraction irréductible.
V2 = p×202
×10 ; V2/ V= 200 / 1525.
200 = 23*52 ; 1525 =52*61
; V2/ V= 8 / 61.
ABCD est un rectangle tel que AB = 30 cm et BC = 24 cm. On colorie aux
quatre coins du rectangle quatre carrés identiques en gris. On délimite
ainsi un rectangle central que l’on colorie en noir.
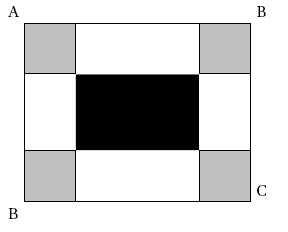
Dans cette question, les quatre carrés gris ont tous 7 cm de côté.Dans
ce cas :
quel
est le périmètre d’un carré gris ?
4*7 = 28 cm.
quel
est le périmètre du rectangle noir ?
Longueur L = AB-2*7 = 30-14 = 16 cm ; largeur = l = BC-2*7
=24-14 = 10 cm.
périmètre du rectangle noir : 2(L+l) =
2(16+10) = 52 cm.
Dans cette question, la longueur du côté des quatre carrés gris peut
varier. Par conséquent, les dimensions du rectangle noir varient aussi.
Est-il
possible que le périmètre du rectangle noir soit égal à la somme des
périmètres des quatre carrés gris ?
On note x la mesure du côté d'un carré gris. Périmètre des 4 carrés
gris : 4*4x = 16 x cm.
L= 30-2x ; l =24-2x
; périmètre du rectangle noir : 2(L+l)
=2(30-2x+24-2x) =108-8x.
108-8x
=16x ;
108 =24 x ; x =108 / 24 =4,5 cm.
|
Flora fait
des bracelets avec de la pâte
àmodeler. Ils sont tous constitués de 8 perles rondes et de 4 perles
longues. Cette pâte à modeler s’achète par blocs qui ont tous la forme
d’un pavé droit dont les dimensions
sont précisées ci-dessous. La pâte peut se pétrir à volonté et durcit
ensuite à la cuisson.
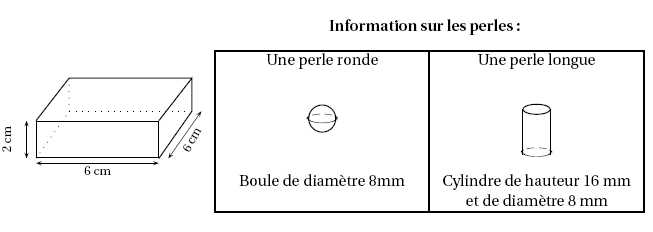
Flora
achète deux blocs de pâte à modeler : un bloc de pâte à modeler bleue
pour faire les perles rondes et un bloc de pâte à modeler blanche pour
faire les perles longues.
Combien
de bracelets peut-elle ainsi espérer réaliser ?
On rappelle les formules suivantes : Volume d’un cylindre : V = p×rayon2
×hauteur
Volume d’une sphère : V =4 / 3p×rayon3.
Volume d'un bloc : 2*6*6 = 72 cm3.
Volume
d'une perle ronde : 4
/ 3p×0,43=0,268
cm3 ; nombre de perles rondes : 72 / 0,268 ~268.
Volume
d'une perle longue :
p×0,42
×1,6=0,804
cm3 ; nombre de perles longues : 72 / 0,804 ~89.
On peut réaliser 89/4 ~ 22 bracelets.
Un oeuf de poule pèse en moyenne 63 grammes. Sachant que :
• le blanc d’oeuf est deux fois plus lourd que le jaune d’oeuf,
• le jaune d’oeuf est deux fois plus lourd que la coquille,
combien
pèse la coquille d’un oeuf de poule ?
On appelle x la masse de la coquille : masse du jaune : 2x ; masse du
blanc : 4 x.
Masse de l'oeuf : x + 2x +4x = 63 ; x = 9 g.
|
QCM.
| Trois mille
trente et trois centimes s'écrit : |
300 030,300 |
3030,300 |
3030,03 |
| 2080+10+10 est
égal à : |
3000 |
2100 |
3100 |
| 3x*2x est égal
à : |
6x |
5x2 |
6x2 |
| 5 10-3
est égal à : |
50-3 |
-5000 |
0,005 |
| Les solutions
de l'équation x(x+7)=0 sont : |
0 et -7 |
0 et 7 |
1 et -7 |
| Racine carrée
16 + racine carrée 9 est égal à : |
4+3=7 |
4½+3½ |
25½
=5 |
Pierre va en
vélo au collège, il part à 6 h 38. Son trajet dure 25 min.
les cours commence à 7 h05. Il arrivera : |
à
l'heure.
6 h38+0h25 =6 h63 ou 7 h03 |
en avance |
en retard |
| Dans un jeu de
52 carte, on tire une carte. Quelle est la probabilité que la carte
soit un as ? |
1/52 |
0,777 |
4 / 52 |
|