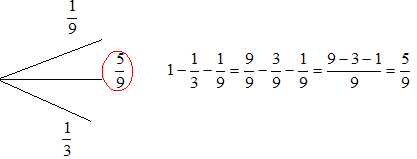Statistiques et probabilités, brevet 2013

Statistiques et probabilités, brevet 2013.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

(sujet 2013)
Les informations suivantes concernent les salaires des hommes et des femmes d’une même entreprise :
Salaires des femmes :
1 200 € ; 1 230 € ; 1 250 € ; 1 310 € ; 1 370 € ; 1 400 € ; 1 440 € ; 1 500 € ; 1 700 € ; 2 100 €.
Salaires des hommes :
Effectif total : 20
Moyenne : 1 769 €
Etendue : 2 400 €
Médiane : 2 000 €
Les salaires des hommes sont tous différents.
Comparer le salaire moyen des hommes et celui des femmes.
Salaire moyen des femmes (1200 +1230 +1250 +1310 +1370 +1400 +1440 +1500 +1700 +2100) /10 =1450 €.
Le salaire moyen des femmes est inférieur au salaire moyen des hommes.
On tire au sort une personne dans l’entreprise. Quelle est la probabilité que ce soit une femme ?
p =ombre de femmes / effectif total = 10/30 =1/3.
Le plus bas salaire de l'entreprise est de 1 000 €. Quel salaire est le plus élevé ?
Salaire le plus élevé chez les hommes : salaire minimum + étendue =1000 +2400 = 3400 €.
Dans cette entreprise combien de personnes gagnent plus de 2 000 € ?
10 hommes gagnent moins de 2000 € et 10 hommes gagnent plus de 2000 €.
10 hommes + une femme = 11 personnes.

Chacune des trois affirmations suivantes est-elle vraie ou fausse ? On rappelle que les réponses
doivent être justifiées.
Affirmation 1 : Vraie.
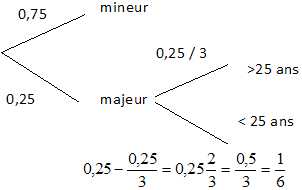
Dans un club sportif, les trois quarts des adhérents sont mineurs et le tiers des adhérents majeurs a
plus de 25 ans. Un adhérent sur six a donc entre 18 ans et 25 ans.

Affirmation 2 : Faux.
Durant les soldes si on baisse le prix d’un article de 30 % puis de 20 %, au final le prix de l’article a baissé de 50 %.
Prix après première remise : 0,70 € pour un prix initial de 1 €.
prix après seconde remise : 0,70-0,70*0,20 =0,56 €.
La remise totale est de 44 %.
Affirmation 3 : Vrai.
Pour n’importe quel nombre entier n , (n + 1 )² – (n – 1 )² est un multiple de 4.
(n + 1 )² – (n – 1 )² =(n+1+n-1)(n+1-(n-1)) =2n *2 = 4 n.

.
.

Soit l'expérience aléatoire suivante :
- tirer au hasard une boule noire, noter son numéro ;
- tirer au hasard une boule blanche, noter son numéro ;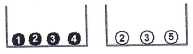
- puis calculer la somme des 2 numéros tirés.
On a simulé I'expérience avec un tableur, en utilisant la fonction ALEA() pour obtenir les numéros des boules tirées au hasard. Voici les résultats des premières expériences :

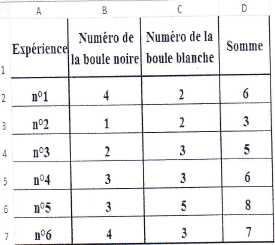
Décris l'expérience n"3.
La boule noire tirée porte le n°2 et la boule blanche tirée porte le n°3. La somme des deux numéros est égale à 5.
Quelle formule est écrite dans la case D5 ?
= B₅ +C₅.
Peut-on obtenir la somme 2 ? Justifie.
Non : le plus petit numéro des boules blanches est 2 et le plus petit numéro des boules noires est égal à 1.
Quels sont les tirages possibles qui permettent d'obtenir la sornme 4 ?
Boule blanche n°2 et boule noire n°2 ; boule blanche n°3 et boule noire n°1 ;
Quelle est la plus grande somme possible ?
Boule blanche n°5 et boule noire n°4 : somme 4+5 = 9.

.

Sur une seconde feuille de calcul, on a copié les résultats obtenus avec 50 expériences, avec 1 000 expériences, avec 5 000 expériences et on a calculé les fréquences des différentes sommes.

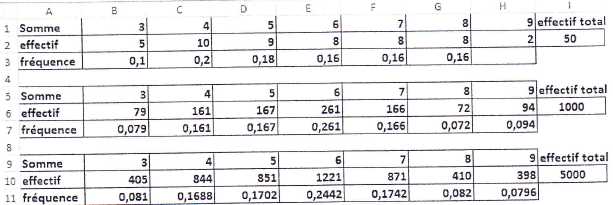
Quelle est la fréquence de la somme 9 au cours des 50 premières expériences ? Justifie.
effectif / effectif total = 2 / 50 = 0,04.
Quelle formule a-t-on écrite dans la case B₇ pour obtenir la fréquence de la somme 3 ?
=B₆ / 1000 ou bien =B₆ /$I$6
Donne une estimation de la probabilité d'obtenir la somme 3.
La somme 3 peut être obtenue uniquement en tirant la boule noire n°1 et la boule blanche n°2.
Probabilité de tirer la boule noire n°1 parmi 4 boules : 1/4 = 0,25.
Probabilité de tirer la boule blanche n°2 parmi 3 boules : 1/3 = 0,33.
Probabilité d'obtenir la somme 3 : 0,25*0,33 ~0,083.

Jeu de fléchettes.
Le jeu de fléchettes consiste à lancer 3 fléchettes sur une cible. La position des fléchettes sur la cible détermine le nombre de points obtenus. La cible est installée de sorte que son centre se trouve à 1,73 m du sol. Les pieds du joueur ne doit pas s’approcher à moins de 2,37 m lorsqu’il lance les fléchettes. Pour cela, un dispositif électronique est installé qui en mesurant l’angle calcule automatiquement la distance du joueur au mûr. Il sonne si la distance n’est pas réglementaire.

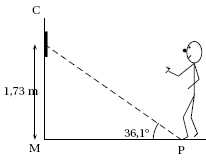
Un joueur s’apprête à lancer une fléchette. La droite passant par le centre de la cible et son pied fait un angle de 36,1° avec le sol. Le mur est perpendiculaire au sol.
Est-ce que la sonnerie va se déclencher ? Justifier la réponse.
tan 36,1 = MC / MP ; MP =MC / tan 36,1 = 1,73 / 0,72921 =2,372 m, valeur supérieure à 2,37 : la sonnerie ne se déclenche pas.
On a relevé dans le tableau ci-dessous les points obtenus par Rémi et Nadia lors de sept parties de fléchettes. Le résultat de Nadia lors la partie 6 a été égaré.

Calculer le nombre moyen de points obtenus par Rémi.
(40 +35+85+67+28+74+28) / 7 =51
Sachant que Nadia a obtenu en moyenne 51 points par partie, calculer le nombre de points qu’elle a obtenus à la 6^e partie.
(12+62+7+100+81+30+x)/7 =51 ; (292+x)/7 =51 ; 292+x = 7*51 =357 ; x = 65.
Déterminer la médiane de la série de points obtenus par Rémi, puis par Nadia.

On considère l’expérience aléatoire suivante : on tire au hasard une carte dans un jeu bien mélangé de 32 cartes (il y a 4 « familles » coeur, trèfle, carreau et pique et on a 8 coeurs, 8 trèfles, 8 carreaux et 8 piques).
On relève pour la carte tirée la « famille » (trèfle, carreau, coeur ou pique) puis on remet la carte dans le jeu et on mélange.
On note A l’évènement : « la carte tirée est un trèfle ».
Quelle est la probabilité de l’évènement A ?
Nombre de trèfle 8, soit 8 cas favorables sur 32 cas possible : p(A) =8/32 = 0,25.
On répète 24 fois l’expérience aléatoire ci-dessus. La représentation graphique ci-dessous donne la répartition des couleurs obtenues lors des vingt-quatre premiers tirages :

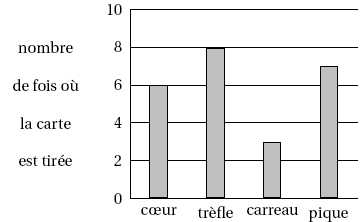
Calculer la fréquence d’une carte de la « famille » coeur et d’une carte de la « famille » trèfle.
f(coeur) = 6/24 =0,25 ; f(trèfle) =8/24 =1/3 ~ 0,33
On reproduit la même expérience. Arthur mise sur une carte de la « famille » coeur et Julie mise sur d’une carte de la « famille » trèfle.
Est-ce que l’un d’entre deux a plus de chance que l’autre de gagner ?
La probabilité de tirer un coeur est la même que celle de tirer un trèfle, c'est à dire 8/32 = 0,25.
Les deux joueurs ont la même chance de gagner.

On considère la série statistique donnant le SMIC horaire brut en euros de 2001 à 2011 (source : INSEE).

Quelle est l’étendue de cette série ? Interpréter ce résultat.
Le smic horaire s'étale de 6,67 € à 9,4 € et croît régulièrement chaque année.
Quelle est la médiane ? 8,27 €.
Paul remarque qu’entre 2001 et 2002, l’augmentation du SMIC horaire brut est de 16 centimes alors qu’entre 2007 et 2008, elle est de 19 centimes.
Il affirme que « le pourcentage d’augmentation en 2011 est supérieur à celui pratiqué entre 2001 et 2002 ». A-t-il raison ?
Pourcentage d'augmentation entre 2007 et 2008 : 0,19 /8,44 = 0,0225 soit 2,25 % .
Pourcentage d'augmentation entre 2001 et 2002 : 0,16 /6,67 ~ 0,024 soit 2,4 %. Il a donc tord.

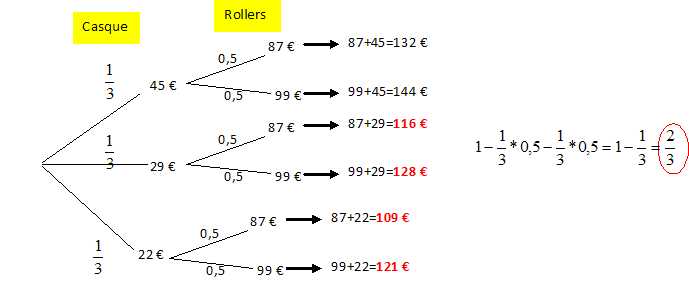
Compléter l'arbre de probabilité ci-dessous.

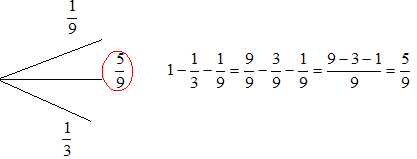
Caroline souhaite s'équiper pour faire du roller. Elle a le choix entre une paire de rollers gris à 87 € et une paire de rollers noire à 99 €. Elle doit choisir un casque parmi 3 modèles dont les prix sont respectivement 45 €, 22 € et 29 €. Elle choisit un casque et une paire de rollers au hasard. Quelle est la probabilité que l'ensemble lui coûte moins de 130 € ?

Elle s'aperçoit qu'en achetant la paire de rollers noire et le casque à 45 € elle bénéficie d'une remise de 20 % sur l'ensemble. calculer le prix payé après remise.
(99+45)*(1-0,2) = 144*0,8 =115,2 €.
La probabilité de payer moins de 130 € devient : 1-1/3 *0,5 = 1-1/6 = 5/6.

menu