Mathématiques,
Diplome national du brevet, Amérique du Sud 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
|
Exercice 1. 5 points.
Dans une urne, il y a huit boules indiscernables au toucher, qui
portent chacune un numéro :
7 ; 7 ; 5 ; 2 ; 7 ; 6 ; 7 ; 4
1. Si on tire au
hasard une boule dans cette urne, quelle est la probabilité qu’elle
porte le numéro 7 ?
4 cas favorables sur 8 cas possibles.
La probabilité de tirer un 7 est 4 / 8 = 0,5.
2. Wacim s’apprête
à tirer une boule. Il affirme qu’il a plus de chance de tirer un numéro
pair qu’un numéro impair.
A-t-il raison ?
Il y a 5 numéros impairs et 3 numéros pairs.
Probabilité de tirer un numéro impair : 5 / 8.
Probabilité de tirer un numéro pair : 3 / 8 < 5 /8. Il n'a pas
raison.
3. Finalement,
Wacim a tiré la boule portant le numéro 5 et la garde : il ne la remet
pas dans l’urne.
Baptiste s’apprête à tirer une boule dans l’urne.
Quelle est la probabilité que cette boule porte le numéro 7 ?
4 cas favorables sur 7 possibilités.
Probabilité de tirer un 7 : 4 / 7.
Exercice 2. 7 points
Madame
Duchemin a aménagé un studio dans les combles de sa maison, ces combles
ayant la forme d’un prisme droit avec comme base le triangle ABC
isocèle en C.
Elle a pris quelques mesures, au cm près pour les longueurs et au degré
près pour les angles. Elle les a reportées sur le dessin ci-dessous
représentant les combles, ce dessin n’est pas à l’échelle.
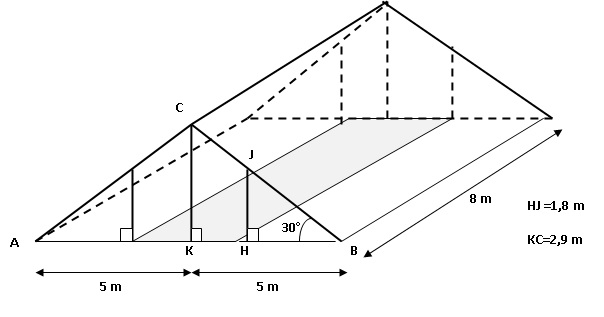
Madame
Duchemin souhaite louer son studio.
Les prix de loyer autorisés dans son quartier sont au maximum de 20 €
par m 2 de surface habitable.
Une surface est dite habitable si la hauteur sous plafond est de plus
de 1,80 m (article R111−2 du code de construction) : cela correspond à
la partie grisée sur la figure.
Madame Duchemin souhaite fixer le prix du loyer à 700 €. Peut-elle
louer son studio à ce prix ?
Dans le triangle BHJ : tan 30 = HJ / BH ;
BH = HJ / tan 30 = 1,8 / 0,577 ~3,12 m.
Donc KH = 5 -3,12 = 1,88 m.
Aire de la surface hachurée : 2 x1,88 x8 ~30,1 m 2.
Prix maximum de la location : 30,1 x20 ~602 €.
Elle ne peut pas louer son studio à 700 €..
|
|
Exercice 3. 6 points
Léa choisit un nombre, le multiplie par 6 puis ajoute 5.
Julie choisit le même nombre, lui ajoute 8, multiplie le résultat par
le nombre de départ, puis soustrait le carré du nombre de départ.
1. Léa et Julie
choisissent au départ le nombre −3.
a. Quel résultat
obtient Léo ?
-3 x6 +5 =-18+5= -13.
b. Quel résultat
obtient Julie ?
(-3 +8)x(-3)- (-3)2 = -15 -9 = -24.
2. Quel nombre positif doivent-ils choisir au départ pour obtenir le
même résultat ?
On note n ce nombre : 6 n +5 = (n+8)n -n2.
6 n+5 =n2+8n-n2 = 8 n.
5 = 2n ; n =2,5.
Exercice 4. 7,5
points.
Indiquer en justifiant si chacune des affirmations suivantes est vraie
ou fausse.
Affirmation 1
: « Les nombres 11 et 13 n’ont aucun multiple commun. » Faux.
11 x13 = 143 est un multiple commun à 11 et 13.
Affirmation 2
: « Le nombre 231 est un nombre premier. » Faux.
231 a pour diviseur 1 ; 3 ; 7 ; 11 ; 33 ; 77 ; 231.
Un nombre premier ne possède que deux diviseurs, 1 et lui même.
Affirmation 3
: « 2 / 15 est le tiers de 6 /15 ». Vrai.
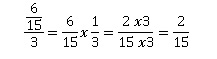
Affirmation 4 :
« 15−5×7+3 = 73 ». Faux.
15 -35 +3 = -17.
Affirmation 5
: « Le triangle ABC avec AB = 4,5 cm, BC = 6 cm et AC = 7,5 cm est
rectangle en B. » Vrai.
AB2 + BC2 = 4,52 +62 =
56,25. AC2 = 56,25.
AB2
+ BC2 = AC2.
Exercice 5. 8
points.
Cet exercice porte sur la consommation d’énergie en France.
Le tableau ci-dessous donne la répartition (exprimée en pourcentages)
de la consommation des différents types d’énergie entre 1973 et 2014.
|
1973
|
1980
|
1990
|
2002
|
2014
|
Electricité
|
4,3
|
11,7
|
36,4
|
41,7
|
45,4
|
Pétrole
|
67,6
|
56,4
|
38,7
|
34,6
|
30,2
|
Gaz
|
7,4
|
11,1
|
11,5
|
14,7
|
14
|
Energies
renouvelables
|
5,2
|
4,4
|
5,0
|
4,3
|
7,0
|
Charbon
|
15,5
|
16,4
|
8,4
|
4,7
|
3,4
|
Source INSEE.
1. Quel pourcentage
de la consommation d’énergie le pétrole représentait-il en 1980 ? 56,4
%.
2. À partir du
tableau précédent, on a créé, pour une des années, un diagramme
représentant la répartition des différents types d’énergie. Déterminer
de quelle année il s’agit.
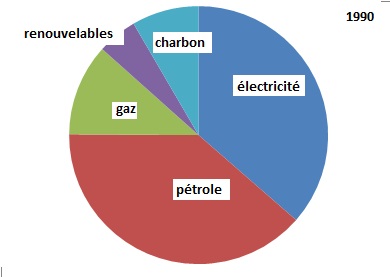
3. On peut observer
l’évolution de la part du pétrole au fil des années à partir d’une
représentation graphique comme celle proposée ci-dessous.
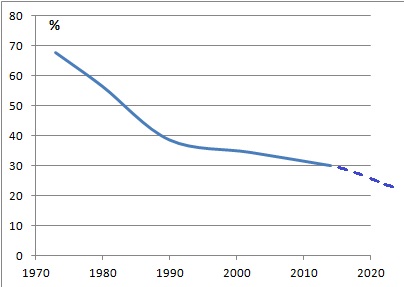
Les pointillés indiquent que l’on suppose que la baisse de la part du
pétrole va se poursuivre sur le rythme observé depuis 2002.
En suivant cette supposition, on peut modéliser la part du pétrole
(exprimée en pourcentage) en fonction de l’année a par la fonction P,
définie ainsi :
P(a) = −17 / 48 a +743,5.
a. Écrire le calcul
permettant de vérifier que P(1990) ~ 38,7.
-17 / 48 x1990 +743,5 ~ -704,8 +743,5 ~ 38,7.
b. D’après
cemodèle, à partir de quelle année la part du pétrole sera-t-elle nulle?
0 = -17 / 48 a +743,5 ; a = 743,5 x48 / 17 ~ 2099.
|
|
|
|
Exercice 6. 6,5
points
Le bloc d’instruction « carré » ci-dessous a été programmé puis utilisé
dans les deux programmes suivants.
.
Définir
carré.
Stylo en position écriture..
Carré
Répéter 4 fois
Avancer de longueur
Tourner de 90° dans le sens contraire des aiguille d'une montre.
Fin repeter.
Relever le stylo |
Programme 1.
Quand le drapeau vert est levé.
mettre longueur à 10
Répéter 4 fois.
Carré
Mettre longueur à longueur +20
Fin répéter.
Cacher. |
Programme 2.
Quand le drapeau vert est levé.
mettre longueur à 10
Répéter 4 fois.
Carré
Mettre longueur à longueur +2
Fin répéter.
Cacher. |
1. Voici trois dessins :
a. Lequel de ces trois dessins obtient-on avec le programme no 1?
b. Lequel de ces trois dessins obtient-on avec le programme no 2?
c. Pour chacun des deux programmes, déterminer la longueur, en pixel,
du côté du plus grand carré
dessiné?
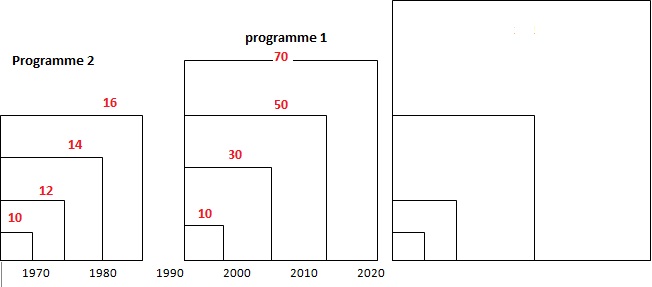
2. On souhaite
modifier le programme n° 2 pour obtenir le dessin ci-dessous.
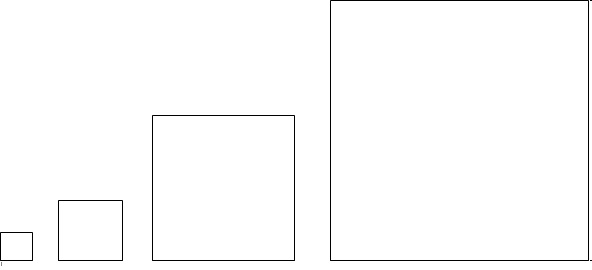
Parmi les trois modifications suivantes, laquelle permet d’obtenir le
dessin souhaité.
Aucune justification n’est attendue pour cette question. Modification 2.
Modification 1.
Quand le drapeau vert est levé.
mettre longueur à 10
Répéter 4 fois.
Carré
Avancer de longueur +10
Mettre longueur à longueur +2
Fin répéter.
Cacher |
Modification 2.
Quand le drapeau vert est levé.
mettre longueur à 10
Répéter 4 fois.
Carré
Mettre longueur à longueur +2
Avancer de longueur +10
Fin répéter.
Cacher |
Modification 3.
Quand le drapeau vert est levé.
mettre longueur à 10
Répéter 4 fois.
Carré
Mettre longueur à longueur +2
Fin répéter.
Avancer de longueur +10
Cacher |
Exercice 7. 5
points.
Le tableau ci-dessous indique l’apport énergétique en kilocalories par
gramme (kcal/g) de quelques nutriments.
Apport énergétique pour quelques nutriments
Lipides 9 kcal/g
Protéines 4 kcal/g
Glucides 4 kcal/g
1. Un oeuf de 50 g
est composé de :
— 5,3 g de lipides ;
— 6,4 g de protéines ;
— 0,6 g de glucides ;
— 37,7 g d’autres éléments non énergétiques.
Calculer la valeur énergétique totale de cetoeuf en kcal.
9 x5,3 + 6,4 x4 +0,6 x4 = 47,7 + 25,6 +2,4 = 75,7 kcal.
2. On a retrouvé
une partie de l’étiquette d’une tablette de chocolat.
Pour 100 g de chocolat :
valeur énergétique : 520 kcal; lipides 30 g ; protéines 4,5 g ;
glucides....
Dans cette tablette de 200 g de chocolat, quelle est la masse de
glucides ?
Pour 200 g de chocolat, la valeur énergétique est de 520 x2 = 1040 kcal.
lipides : 60 x 9 = 540 kcal ;
protéines : 9 x 4 = 36 kcal ;
glucides : 1040 -540 -36 = 464 kcal.
Masse de glucides : 464 / 4 =116 g.
|
|
|