Mathématiques, Brevet Polynésie 2017.

Mathématiques, Brevet Polynésie 2017.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1 (7 points) QCM.
1. Combien faut-il environ de CD de 700 Mo pour stocker autant de données qu'une clé de 32 Go ?
46 ; 4600 ; 4 600 000.
32 000 / 700 ~ 46.
2. La diagonale d'un rectangle de 10 cm par 20 cm est d'environ :
15 cm ; 22 cm ; 30 cm.
10² +20² = 500 ; prendre la racine carrée de 500 : ~22 cm.
3. Une solution de l'équation 2x+3 =7x-4 est : 5 /7 ; 1,4 ; -0,7.
3+4 = 7x-2x ; 7 = 5 x ; x = 7 / 5 = 1,4.
4. La fraction irréductible de 882 / 1134 est : 14 / 9 ; 63 / 81 ; 7 / 9.

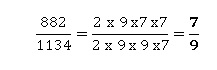5. On considère la fonction f(x) = 3x+4.
Quelle formule doit-on entrer en B2 puis recopier vers la droite afin de calculer les images des nombres de la ligne 1 par la fonction f.
= 3*A1+4 ; =3*5+4 ; =3*B1+4.

A
B
C
D

1
x
5
6
7

2
f(x)

.
.

Exercice 2 : (8 points)
Un TGV est composé de 2 rames.
Chaque rammes est composée de 2 motrices de type A encadrant dix voitures de type B.
Longueur d'une motrice : 19 m ; longueur d'une voiture : 18,3 m.
Tout le train est passé devant moi en 13 s 53 centièmes.
A quelle vitesse ( en km / h) est -il passé sans s'arrêter devant moi ?
Longueur du train ( 2 x( 2 x19 +10 x18,3) =442 m.
Vitesse ( m/s) = distance (m) / durée (s) = 442 /13,53 ~ .32,67 m /s ou 32,67 x3,6 ~118 km /h.

....

.....
Exercice 3 (9 points)
1. Tracer un triangle CDE rectangle en D tel que CD = 6,8 cm et DE = 3,4 cm.
Calculer CE au dixième près.
CE² = CD² +DE² = 6,8² +3,4² = 57,8 ; CE ~7,6 cm.
2. Placer le point F sur [CD) tel que CF = 2 cm.
Placer le point G sur (CE] tel que FG = 1 cm.
Les droites (FG) et (DE) sont-elles parallèles ?

Deux points G₁ et G₂ sont possibles.
D'après la figure, les droiites (DE) et FG₁) ne sont pas parallèles.
Dans le triangle EDC rectangle en D : tan a = ED / CD = 3,4 / 6,8 =0,5.
Hypothèse : ( ED) et (FG₂) sont parallèles.
Dans le triangle CFG₂ rectangle en F : tan a =FG₂ / CF = 1 / 2 =0,5.
L'hypothèse est vérifiée.

Exercice 4 ( 6 points).
Le baklava est une pâtisserie. Dans un sachet non transparent, on a 7 baklavas indiscernables au toucher portant les lettres du mot BAKLAVA.
On tire au hasard un gâteau dans ce sachet et on regarde la lettre inscrite sur le gâteau.
1. Quelle sont les issues de ce tirage ?
A ; B ; K ; L ; V.
2. Déterminer les probabilités suivantes :
la lettre tirée est un L : 1 /7.
La lettre tirée n'est pas un A : 4 / 7.
3. Enzo achète un paquet contenant 10 baklavas tous indiscernables au toucher. Ce sachet contient 2 baklava à base de pistache, 4 kaklava à base de noisettes et les autres baklavas sont à base de noix. Enzo pioche un gâteau au hasard et le mange ; c'est un gâteau à base de noix. Il souhaite en manger un autre.
Son amie Laura affirme que, s'il veut maintenant prendre un nouveau gâteau, il aura plus de chances de piocher un gâteau à base de noix. A-t-elle raison ? Justifier.
Le paquet contient 2 baklavas à base de pistache, 4 kaklavas à base de noisettes et 3 baklavas à base de noix.
Probabilité de tirer un gâteau à base de noix : 3/9 = 1 /3 ~0,33.
Probabilité de tirer un gâteau à base de noisette : 4 / 9 ~0,44.
Probabilité de tirer un gâteau à base de pistache : 2 / 9 ~0,22.
Laura a tord.

.
.

Exercice 5 : (7 points)
On considère le programme de calcul suivant :
Choisir un nombre.
Le multiplier par -4.
Ajouter 5 au résultat.
1. Vérifier que si on choisit -2 ce programme donne 13.
(-2) x(-4) +5 = 8 +5 = 13.
2. Quel nombre faut-il choisir au départ pour obtenir -3 ?
-4 x +5 = -3 ; 4x = 5+3 ; x = 2.
3. Salomé fait exécuter le script suivant :
Demander choisir un nombre et attendre
Si -4 *réponse +5 <0 alors dire Bravo.
Sinon dire Essaie encore.
Quelle sera la réponse si on choisit 12 ?
-4 x12 +5 = -43, donc Bravo.
Quelle sera la réponse si on choisit -5 ?
-4 x(-5) +5 =25, donc Essaie encore.
4. Ce programme de calcul peut se traduire par l'expression littérale -4x+5 avec x représentant le nombre choisi.
Résoudre l'équation -4x+5 <0.
5 < 4x ; 5 / 4 < x soit x > 1,25.
5. A quelle condition, portant sur le nombre choisi, est-on certain que la réponse sera Bravo ?
Le nombre choisi doit être supérieur à 1,25.

Exercice 6 : (8 points)
On donne le plan de deux lignes de bus.

C'est à 6 h 30 que les deux bus des lignes 1 et 2 passent à l'arrêt ""Mairie" dans le sens des aiguilles d'une montre. Le bus de la ligne 1 met 3 minutes entre chaque arrêt ( temps de stationnement compris ), tandis que le bus de la ligne 2 met 4 minutes. Tous les deux vont effectuer le circuit complet un grand nombre de fois. Ils s'arrêteront juste après 20 h.
Est-ce que les deux bus vont se retrouver à un moment de la journée à l'arrêt "Mairie" en même temps ? Si oui, donner tous les horaires précis de ces rencontres.
Le bus 1 met 8 x3 = 24 minutes pour parcpourir la ligne 1.
Le bus 2 met 8 x4 =32 minutes pour parcourir la ligne 2.
Durée de circulation des bus : 20 h -6 h 30 = 13 h 30 soit 13 x 60 +30 = 810 minutes.
24 = 2³ x3 ; 32 = 2⁵ ; Plus Petit Multiple Commun à 24 et 32 = 32 x3 = 96.
Les multiples communs à 24 et 32 inférieurs à 810 sont :
96 ; 192 ; 288 ; 384 ; 480 ; 576 ; 672 ; 768.
Horaires de ces rencontres : 6 h 30 min + 96 min 6 h 30 min +1 h 36 min = = 8 h 06 min.
8 h 06 min +1 h 36 min = 9 h 42 min.
9 h 42 min + 1 h 36 min = 11 h 18 min.
11 h 18 min + 1 h 36 min = 12 h 54 min.
12 h 54 min + 1 h36 min = 14 h 30 min.
14 h 30 min + 1 h36 min = 16 h 06 min.
16 h 06 min + 1 h 36 min = 17 h 42 min.
17 h 42 min + 1 h36 min = 19 h 18 min.

.

menu