Mathématiques, brevet Amérique du Nord 2017 .

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.



. .



.
.


1. Recopier la bonne réponse.
La somme suivante est égale à :
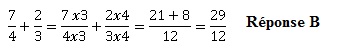
L'équation 5x+12 = 3 a pour solution :
5x = 3-12 ; x = -9 / 5= -1,8. Réponse C.
Une valeur approchée au dixième près du nombre suivant est :


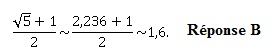2. Avec un logiciel de géométrie, on exécute le programme suivant :
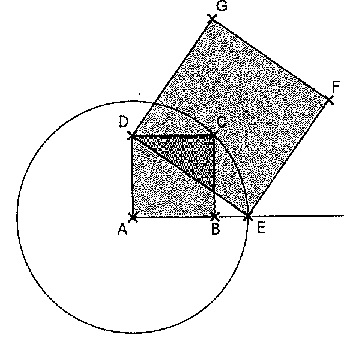
Construire un carré ABCD.
Tracer le cercle de centre A et de rayon [AC]
Placer le point E à l'intersection du cercle et de la demi-droite (aB).
Construire le carré DEFG.

1. Réaliser la construction avec AB = 3 cm.
2. Dans cette question AB = 10 cm.
a. Montrer que AC = racine carrée (200) cm.
ABC est un triangle rectangle isocèle en B.
AC2 = AB2 +BC2 = 102 +102 = 200 ; AC = racine carrée (200) cm.
b. Expliquer pourquoi AE = racine carrée (200) cm.
AC et AE sont les rayons d'un même cercle.
c. Montrer que l'aire du carré DEFG est le triple de l'aire du carré ABC.
Aire du carré ABC = 10 x10 = 100 cm2.
Le triangle DAE est rectangle en A.
DE2 = AD2 +AE2 = 102 +200 =300  cm2.
L'aire du carré DEFG est égale à DE2 = 300 cm2.
3. On admet pour cette question que pour n'importe quelle longueur du côté (AB], l'aire du carré DEFG est toujours le triple de l'aire du carré ABCD.
On souhaite obtenir un carré DEFG ayant une aire de 48 cm2. Quelle longueur AB faut-il choisir ?
Aire du carré ABCD = 48 / 3 = 16 cm2. AB = 4 cm.
.
.

....

.....
 3. Probabilités.
Il y a dans une urne 12 boules indiscernables, numérotées de 1 à 12. On tire une boule au hasard.
1. Est-il plus probable d'obtenir un numéro pair ou bien un multiple de 3 ?
 Nombre pair : 2 ; 4 ; 6 ; 8 ; 10 ; 12.
Probabilité de tirer un numéro pair = 6 / 12 = 0,5.
Multiple de 3 : 3 ; 6 ; 9 ; 12.
Probabilité de tirer un multiple de 3 = 4 / 12 = 1 /3.
Il est plus probable de tirer un numéro pair que de tirer un multiple de 3.
2. Quelle est la probabilité d'obtenir un numéro inférieur à 20 ?
12 cas favorables sur 12 possibilités. La probabilité d'obtenir un numéro inférieur à 20 vaut 1.
3. On enlève de l'urne toutes les boules dont le numéro est un diviseur de 6. On tire à nouveau une boule au hasard. Expliquer pourquoi la probabilité d'obtenir un numéro qui soit un nombre premier est alors 0,375.
Numéros retirés : 1 ; 2 ; 3 ; 6.
Numéros restants : 4 ; 5 ; 7 ; 8 ; 9 ; 10 ; 11 ; 12.
Nombres premiers restants : 5 ; 7 ; 11.
3 cas favorables sur 8 cas possibles.
Probabilité de tirer un nombre premier : 3 / 8 = 0,375.

4. Les données et les questions de cet exercice concernent la France métropolitaine.
En 2015, environ 4,7 % de la population française souffrait d'allergies alimentaires.
En 2010, les personnes concernées par les allergies alimentaires étaient deux fois moins nombreuses qu'en 2015.
En 1970, seulement 1% de la population était concernée.

Partie 1.
1. Déterminer une estimation du nombre de personnes, à 100 000 près, qui souffraient d'allergies alimentaires en France en 2010.
Population française en 2015 : 61 000 000.
Personnes souffrant d'allergies alimentaires en 2015 :
61 000 000 x4,7 / 100 ~2 867 000.
personnes souffrant d'allergies alimentaires en 2010 :
 2 867 000 / 2 = 1 433 500 ~ 1 400 000.
2. Est-il vrai qu'en 2015, il y avait environ 6 fois plus de personnes concernées qu'en 1970 ?.
Population française en 1970 : 50 500 000.
Nombres de personnes souffrant d'alergies alimentaires en 1970 : 505 000.
2 867 000 / 505 000 ~5,7. environ 6. L'affirmation est vraie.
...




Partie II..
En 2015, dans un collège de 681 élèves, 32 souffraient d'allergies alimentaires. le tableau suivant indique le type d'aliments auxquels ils réagissent.
Aliments
 lait
 Fruits
 Arachides
 Poisson
 Oeuf
Nombre élèves concernés
 6
 8
 11
 5
 9

1. La proportion des élèves de ce collège souffrant d'allergies alimentaires est-elle supérieure à celle de la population française ?
32 / 681 x100 ~4,7 %, valeur identique à la proportion d'allergies alimentaires dans la population française en 2015.
2. Jawad est étonné : " j'ai additionné tous les nombres indiqués dans le tableau et j'ai obtenu 39 au lieu de 32". Expliquer cette différence.
Certains élèves sont allergiques à plusieurs produits alimentaires.
3. Lucas et margot ont commencé un diqgramme pour représenter les allergies des 32 élèves de leur collège..
a. Qui de Lucas ou de margot a fait le choix le mieux adapté à la situation ? Justifier.
Reproduire et terminer le diagramme choisi.
Le diagramme de Lucas est plus lisible que celui de Margot.
5. L'image ci-dessous représente la position obtenu au déclenchement du bloc départ d'un programme de jeu.
L'arrière plan est constitué de points espacé de 40 unités.
Dans cette position le chat a pour coordonnées (-120 ; -80).
Le but du jeu est de positionner le chat sur la balle.

 1. Quelles sont les coordonnées du centre de la balle ?
4 x40 = 160 ; 3 x40 = 120.
2. Dans cette question, le chat est dans la position obtenue au déclenchement du bloc départ. Voici le script du lutin chat qui se déplace.
Quand flèche gauche est cliqué ajouter -40 à x
Quand flèche droite est cliqué ajouter 80 à x.
Quand flèche haut est cliqué ajouter 80 à y.
Quand flèche bas est cliqué ajouter -40 à y.
a. Expliquer pourquoi le chat ne revient pas à la position de départ si le joueur appuie sur la touche --> puis sur la touche <--.
--> conduit à x+80 et --> conduit à (x+80)-40 = x+40.
b. Le joueur appuie sur la succession de touches suivante -->  --> , vers le haut , <--, vers le bas.
Quelles sont les coordonnées du chat après ce déplacement ?
Position initiale ; x = 160 ; y = 120.
Position après2 flèches à droites : x =160+80+80 =320 ; y = 120.
Position apprès une flèche vers le haut : x = 320 ; y = 120 +80 = 200.
Position après <-- : x = 320-40 = 280 ; y = 200.
Position après fléche vers le bas :x = 280 ; y = 200-40 = 160.
c. Parmi les propositions ci-dessous laquelle permet au chat d'atteindre la balle ?










6. Le schéma ci-dessous représente le jardin de Leïla. Il n'est pas à l'échelle.
[OB] et [OF] sont des murs, OB = 6 m et OF = 4 m.

La ligne pointillée BCDEF représente le grillage que Leïla veut installer pour délimiter un enclos rectangulaire OCDE.
Elle dispose d'un rouleau de 50 m de grillage qu'elle veut utiliser entièrement. Elle envisage plusieurs possibilités pour placer le point C.
1. En plaçant C pour que BC = 5 m, elle obtient que EF = 15 m.
a. Vérifier qu'elle utilise les 50 m de grillage.
CD = OF +EF = 4 +15 = 19 m ; ED = OB +BC = 6 +5 = 11 m.
FE +ED +CD +BC = 15 +11 +19 +5 = 50 m.
b. Justifier que l'aire A de l'enclos OCDE est 209 m2.
A = ED x CD = 11 x 19 =209 m2.
2. Pour avoir une aire maximale, le proffesseur lui écrit : " en notant BC = x, on a A(x) = -x2 +18x +144".
Vérifier que cette formule est cohérente avec le résultat de la question 1.
A(5) = -25 +18 x5 +144 =209 m2.
3.a. Leïla a saisi une formule en B2 puis l'a étirée jusqu' à la cellule I2.

Quelle formule est alors inscrite dans la cellule F2 ?
=-F1*F1+18*F1+144
b. Parmi les valeurs du tableau, quelle est celle que Leïla va choisir pour BC afin d'obtenir un enclos d'aire maximale ?
A = 225 m2 ; x = 9 m.
c. Donner les dimensions de l'enclos obtenu.
ED = OB +BC = 6 +9 = 15 m. CD = 225 / 15 = 15 m.

.


  

menu