Mathématiques,
Brevet des collèges Amérique du Sud 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1. QCM
1. Le produit 76
×76 est égal à 76+6 = 712.
2. La superficie
d’une maison a été augmentée de 40%. Elle est désormais de 210 m2.
Sa superficie avant l’augmentation était égale à :
S x1,4 = 210 ; S =210 /1,4 = 150 m2.
3. La probabilité
d’obtenir un diviseur de 6 lors d’un lancer de dé équilibré à 6 faces
numérotées
de 1 à 6 est égale à :
Les diviseurs de six sont : 1 ; 2 ; 3 ; 6.
4 cas favorables sur 6 possibilités ; probabilité d'obtenir un diviseur
de six : 4 / 6 = 2 /3.
Exercice 2.
Un avion de ligne transportant des
passagers atterrit à l’aéroport international Galeao
à Rio de Janeiro. On étudie la distance de freinage de l’appareil en
fonction de sa vitesse au moment de l’atterrissage.
Le pilote peut décider d’un freinage « rapide » s’il souhaite
raccourcir la distance de freinage, ou d’un freinage « confort » plus
modéré et donc plus confortable pour les passagers.
Les courbes suivantes donnent la distance de freinage d’un avion en
fonction de sa vitesse au moment de l’atterrissage selon le mode
freinage choisi (confort ou rapide).
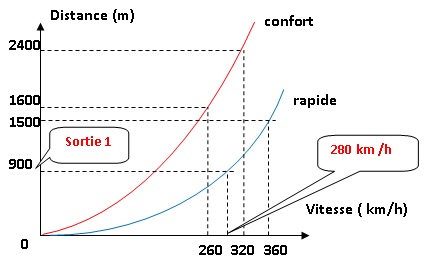
1. Donner par
lecture graphique, sans justification :
a. Une valeur
approchée de la distance de freinage « confort » de l’appareil si
l’avion arrive à une vitesse de 320 km.h−1. 2400 m.
b. Une valeur
approchée de la vitesse d’atterrissage d’un avion dont la distance de
freinage « rapide » est de 1 500 m. 360 km /h.
2. Pour regagner la
zone de débarquement des passagers, l’avion doit emprunter une des
quatre sorties précisées ci-dessous :
Distance des sorties au point d'atterrissage :
Sortie 1 : 900 m ; sortie 2 : 1450 m ; sortie 3 : 2050 m ; sortie 4 :
2950 m.
a. L’avion atterrit
à 260 km.h−1. Le pilote décide un freinage « confort ». Avec
la distance de freinage correspondante, quelle est ou quelles sont les
sorties qu’il va dépasser ?
L'avion parcourt 1600 m ; il dépasse les sorties 1 et 2.
b. Seule la sortie
1 étant disponible, le pilote envisage un freinage « rapide ».
Déterminer avec la précision du graphique, la vitesse maximale avec
laquelle il peut atterrir pour pouvoir emprunter cette sortie.
La distance maximale d'atterrissage rapide est de 900 m ; la vitesse
maximale sera de 280 km /h.
|
| ... |
|
|
Exercice 3.
Carole
souhaite réaliser une mosaïque sur un mur de sa maison. La surface à
paver est un rectangle de dimensions 108 cm et 225 cm et doit être
entièrement recouverte par des carreaux de faïence carrés de même
dimension sans découpe.
1. Carole
peut-elle utiliser des carreaux de 3 cm de côté ? De 6 cm de côté ?
3 est un diviseur de 108 et de 225 ; 6 n'est pas un diviseur de 225.
Elle peut utiliser des carreaux carré de 3 cm de côté. Les catteaux de
6 cm de ccôté nécessiteront une découpe.
2. Quelle est la
dimension maximale des carreaux que Carole peut poser ? Combien de
carreaux utilisera-t-elle ?
108 = 22 x 33 ; 225 = 32 x52.
Le PGCD de 108 et 225 est égal à 9. Les plus grands carreaux
carrés utilisables auront 9 cm de côté. Il lui en faudra :
108 / 9 = 12 en largeur et 225 / 9 = 25 en hauteur.
12 x 25 = 300.
Exercice 4.
TCristo
Redentor, symbole brésilien, est une grande statue dominant la ville de
Rio qui s’érige au sommet du mont Corcovado. Au pied du monument,
Julien et Magali souhaitent mesurer la hauteur de la statue (socle
compris). Julien qui mesure 1,90 m, se place debout à quelques mètres
devant
la statue. Magali place le regard au niveau du sol de telle manière
qu’elle voit le sommet
du Cristo (S) et celui de la tête de Julien (T) alignés ; elle se situe
alors à 10 m de la statue et à 50 cm de Julien. La situation est
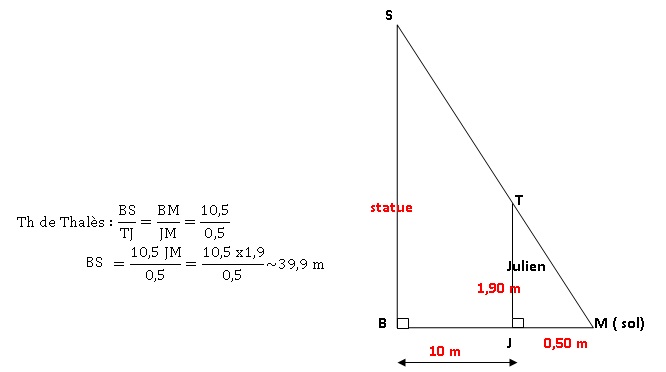
modélisée ci-dessous par la figure qui n’est pas à l’échelle.
Déterminer la hauteur SC de la statue en supposant que le monument et
Julien sont
perpendiculaires au sol.
|
|
|
|
Exercice 5.
Pourmonter
au sommet du Corcovado et accéder à la statue depuis le centre de Rio,
on peut emprunter un minibus. Le prix d’un billet en Réal brésilien
(R$), monnaie brésilienne, comprend le transport vers le site ainsi que
l’accès au monument.
HAUTE SAISON
Total à payer : 329 R$
Entrée valable pour le : 09/02/2016
4 adultes ; 3 enfants de 6 à 11 ans ; 2 enfants de moins de 6 ans.
TARIFS (à partir de 11 ans)
R$ 51,00 Basse saison *
R$ 62,00 Haute saison *
* Tarif réduit pour les enfants de 6 ans à 11 ans.
Gratuit pour les enfants de moins de 6 ans.
1. Déterminer
le prix de la visite pour un adulte le 09/02/2016.
2. Déterminer le
prix de la visite pour un enfant ayant entre 6 ans et 11 ans, le
09/02/2016.
R$ 62,00 prix pour un adulte et x : prix
pour un enfant de 6 à 11 ans.
4* 62+3x = 329 ; 3x=329-248 =81 ; x = 81 / 3 = 27.
Exercice 6.
Inauguré
en 1950, le stade Maracanà est un lieu mythique, place de grands
événements sportifs tels que la coupe dumonde 2014 ou les jeux
olympiques 2016. C’est une structure de forme ovale de dimensions 317 m
et 279 m pour une hauteur de 32 m dont la surface au sol est d’environ
69 500 m2.
Sur la célèbre plage de Copacabana, à Rio, on peut admirer de
nombreuses sculptures de sable.
L’un des sculpteurs souhaite réaliser une reproduction du stade à
l’échelle 1/300.
1. Quelles seront
les dimensions arrondies au centimètre de cette reproduction.
317 / 300 ~ 1,06 m ; 279 / 300 = 0,93 m ; 32 /300 ~0,106 m ~ 11 cm.
2. a. Quelle en
sera la superficie ? On donnera le résultat en m2, arrondi
au centième.
69 500 / 3002 =0,77 m2.
b. Le sculpteur
dispose d’un espace de 1 m2. Est-il certain de pouvoir
réaliser sa reproduction ? On justifiera brièvement la réponse.
Oui, si l'espace au sol est un rectangle de longueur voisine de 1,06 m
et de largeur voisine de 0,93 m.
Non, si l'espace au sol est un carré de 1 m de côté.
|
|
Exercice 7.
Le
mont du Pain de Sucre est un pic situé à Rio à flanc de mer. Il culmine
à 396 mètres d’altitude et est accessible par un téléphérique composé
de deux tronçons. n a représenté ci-dessus le deuxième tronçon du
téléphérique qui mène du point U au sommet S du pic.
On donne : Altitude du point S : 396 m US = 762 m
Altitude du point U : 220 m Le triangle UOS est rectangle en O.
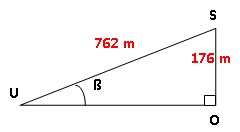
1. Déterminer
l’angle �OUS que forme le câble du téléphérique avec l’horizontale. On
arrondira le résultat au degré.
sin ß = 176 / 762 = 0,231 ; ß ~13°.
2. Sachant que le
temps de trajet entre les stations U et S est de 6 min 30 s, calculer
la vitesse moyenne du téléphérique entre ces deux stations en mètres
par seconde. On arrondira le résultat au mètre par seconde.
6 min 30 = 6 x60 +30 = 390 s ; vitesse moyenne = 762 / 390 =1,954 ~2 m
/s.
3. On a relevé la
fréquentation du Pain de Sucre sur une journée et saisit ces
informations dans une feuille de calcul d’un tableur.
H2=SOMME(B2:G2)
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
1
|
Horaires
|
8
:00 - 10:00
|
10;00
- 12:00
|
12
- 14
|
14
- 16
|
16
- 18
|
18
- 20
|
|
2
|
Nombre
de visiteurs
|
122
|
140
|
.......
|
63
|
75
|
118
|
615
|
On a saisi dans la
cellule H2 la formule : =SOMME(B2:G2)
a. Interpréter le
nombre calculé avec cette formule.
Il s'agit du nombre total de visiteurs.
b. Quel est le
nombre de visiteurs entre 12 h 00 et 14 h 00 ?
615-(122 +140+63 +75 +118)=97.
4. Une formule doit
être saisie pour calculer le nombre moyen de visiteurs par heure sur
cette journée. Parmi les propositions suivantes, recopier sans
justification
celle qui convient : MOYENNE(B2:G2) ; =MOYENNE(B2:G2) ;
MOYENNE(B2:G2)/2 ; =MOYENNE(B2:G2)/2.
Le signe = doit précéder le mot MOYENNE.
L'intervalle de temps étant de deux heures, il faudra diviser la
moyenne par 2 afin de l'exprimer en nombre moyen de visiteurs par heure.
|
|