Mathématiques,
Brevet des collèges Métropole 2016
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Une
société commercialise des composants électroniques qu’elle fabrique
dans deux usines. Lors d’un contrôle de qualité, 500 composants sont
prélevés dans chaque usine et sont examinés pour déterminer s’ils sont
« bons » ou « défectueux ». Résultats obtenus pour l’ensemble des 1 000
composants prélevés :
Usine A : 473 bons et 27 défectueux.
Usine B : 462 bons et 38 défectueux.
1. Si on prélève un composant
au hasard parmi ceux provenant de l’usine A, quelle est la probabilité
qu’il soit défectueux Nombre de composants défectueux / nombre total de
composant =27 / 500 =0,054.
2. Si on prélève un
composant au hasard parmi ceux qui sont défectueux, quelle est la
probabilité qu’il provienne de l’usine A ?
Nombre de composants défectueux issus de A / Nombre total decomposants
défectueux = 27 /(27+38)=0,4153 ~0,42.
3.
Le contrôle est jugé satisfaisant si le pourcentage de composants
défectueux est inférieur à 7% dans chaque usine. Ce contrôle est-il
satisfaisant ?
Probabilité qu'un composant issu de A soit défectueux : 0,054 ( 5,4 %).
Probabilité qu'un composant issu de B soit
défectueux :38 / 500 = 0,076 ( 7,6 %).
Le contrôle n'est pas jugé satisfaisant.
Exercice 2.
On considère les deux programmes de calcul ci-dessous.
Programme A : choisir un nombre. Multiplier
par −2. Ajouter 13.
Programme B : choisir
un nombre. Soustraire 7. Multiplier
par 3.
1. Vérifier qu’en choisissant 2 au
départ avec le programme A, on obtient 9.
2 x(-2) +13 = -4 +13 = 9.
2. Quel nombre
faut-il choisir au départ avec le programme B pour obtenir 9 ?
On note x ce nombre : (x-7) *3 =9 ; 3x-21 = 9 ; 3x = 30 ; x = 10.
3. Peut-on trouver
un nombre pour lequel les deux programmes de calcul donnent le même
résultat ?
Soit x ce nombre : le programme A donne : -2x+13 ;
Le programe B donne : (x-7)*3= 3x-21
-2x+13 = 3x-21 ; 5x = 13+21 ; x = 34 /5 = 6,8.
On peut trouver un nombre entier pour
lequel les deux programmes donnent le même résultat.
|
...
|
|
|
Exercice 3.
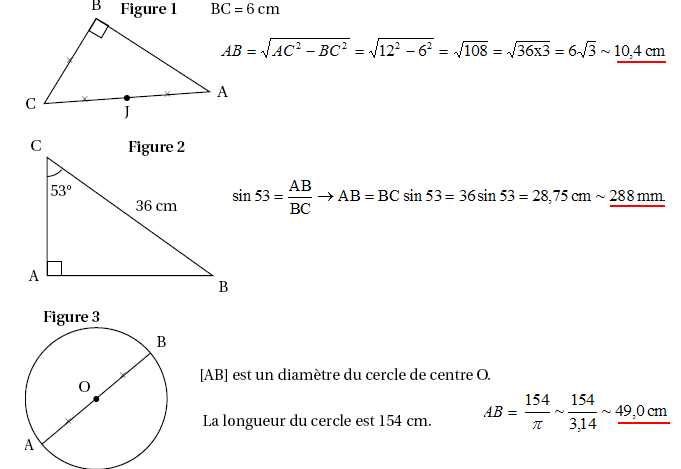
Trois figures codées sont données ci-dessous. Elles
ne sont pas dessinées en vraie grandeur.
Pour chacune d’elles, déterminer la longueur AB au millimètre près.
Exercice 4.
Lors des soldes, un
commerçant décide d’appliquer une réduction de 30% sur l’ensemble des
articles de son magasin.
1. L’un des
articles coûte 54 € avant la réduction. Calculer son prix après la
réduction.
54 (1-0,3) = 54 x 0,7 = 37,8 €.
2. Le commerçant
utilise la feuille de calcul ci-dessous pour calculer les prix des
articles soldés .
|
A |
B |
C |
D |
E |
F |
| 1 |
Prix
avant réduction |
12,00 |
14,80 |
33,00 |
44,20 |
85,50 |
| 2 |
Réduction
de 30 % |
3,60 |
4,44 |
9,90 |
13,26 |
25,65 |
| 3 |
Prix
soldé |
|
|
|
|
|
a. Pour
calculer la réduction, quelle formule a-t-il pu saisir dans la cellule
B2 avant de l’étirer sur la ligne 2 ?
=B1 *0,3
b. Pour obtenir le
prix soldé, quelle formule peut-il saisir dans la cellule B3 avant de
l’étirer sur la ligne 3 ?
=B1 *0,7 ou
bien =B1-B2.
3. Le prix soldé d’un article est
42,00 €. Quel était son prix initial ?
42,00 / 0,70 =60 €.
|
|
|
|
Exercice 5.
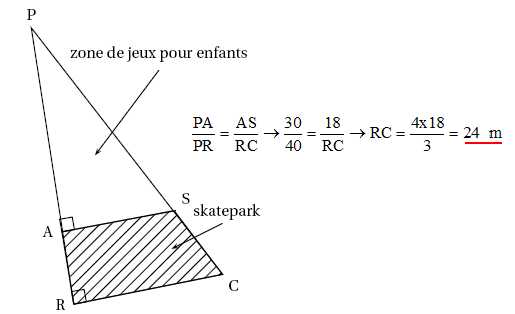
La figure PRC ci-dessous représente un terrain appartenant à une
commune.
Les points P, A et R sont alignés. Les points P, S et C sont alignés.
Il est prévu d’aménager sur ce terrain :
• une « zone de jeux pour enfants » sur la partie PAS ;
• un « skatepark » sur la partie RASC.
On connaît les dimensions suivantes : PA = 30 m; AR = 10 m; AS = 18 m.
1.
La commune souhaite semer du gazon sur la « zone de jeux pour enfants
». Elle décide d’acheter des sacs de 5 kg de mélange de graines pour
gazon à 13,90 € l’unité. Chaque sac permet de couvrir une surface
d’environ 140 m2.
Quel budget doit prévoir cette commune pour pouvoir semer du gazon sur
la totalité de la « zone de jeux pour enfants » ?
Aire de la zone de jeu ( triangle rectangle en A) : PA *AS / 2 = 30 x
18 /2 = 270 m2.
Nombre de sacs : 270 / 140 = 1,93 soit 2 sacs.
Coût : 2 x13,90 = 27,8 €.
2. Calculer l’aire
du « skatepark »
Aire du triangle PRC rectangle en R : PR * RC / 2 = 40 x24 / 2 = 480 m2.
Aire du skatepark : 480 - 270 = 210 m2.
Exercice 6.
Avec des ficelles de 20 cm, on construit des polygones comme ci-dessous
:
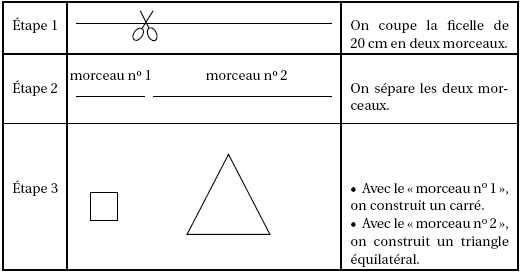
Partie 1 :
Dans cette partie, on découpe à l’étape 1 une ficelle pour que le
«morceau n° 1 » mesure 8 cm.
1. Dessiner en
grandeur réelle les deux polygones obtenus.
2. Calculer l’aire
du carré obtenu.
Côté du carré : 8 / 4= 2 cm ; aire du carré : 2 x2 = 4 cm2.
3. Estimer l’aire
du triangle équilatéral obtenu en mesurant sur le dessin.
Côté du triangle équilatéral : (20-8) / 3 = 4 cm.
Hauteur mesurée de ce triangle ~3,5 cm.
Aire du triangle : 4 x 3,5 / 2 = 7 cm2.
Partie 2 :
Dans
cette partie, on cherche maintenant à étudier l’aire des deux polygones
obtenus à l’étape 3 en fonction de la longueur du «morceau n° 1 ».
1. Proposer une
formule qui permet de calculer l’aire du carré en fonction de la
longueur du «morceau n° 1 ».
On note x la longueur du morceau n° 1. Côté du carré : x / 4 ; aire du
carré : x2 /
16.
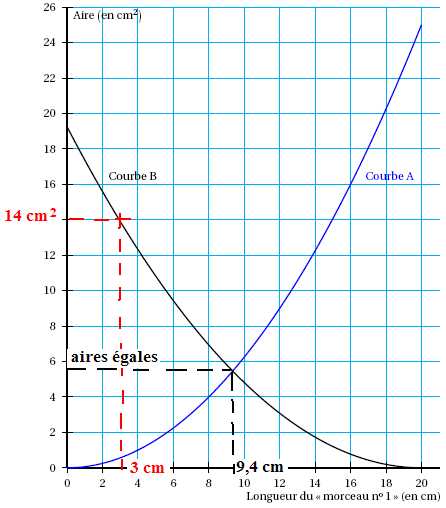
2. Sur le graphique
ci-dessous :
• la courbe A représente la fonction qui donne l’aire du carré en
fonction de la longueur du «morceau n° 1 » ;
• la courbe B représente la fonction qui donne l’aire du triangle
équilatéral en fonction de la longueur du «morceau n° 1 ».
En utilisant ce graphique, répondre aux questions suivantes. Aucune
justification n’est attendue.
a. Quelle est la
longueur du «morceau n°1 » qui permet d’obtenir un triangle équilatéral
d’aire 14 cm2 ?
b. Quelle est la
longueur du «morceau n° 1 » qui permet d’obtenir deux polygones d’aires
égales ?
|
|
Exercice 7.
Antoine
crée des objets de décoration avec des vases, des billes et de l’eau
colorée.
Pour sa nouvelle création, il décide d’utiliser le vase et les billes
ayant les caractéristiques suivantes :
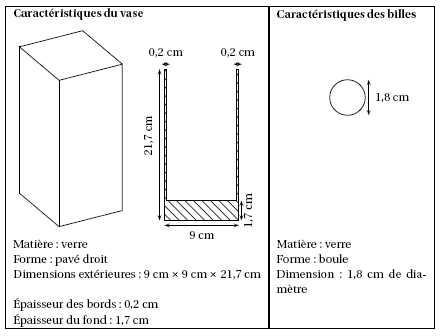
Il met 150 billes dans le vase. Peut-il ajouter un litre d’eau colorée
sans risquer le débordement ?
Dimensions intérieures du vase : 9-0,2-0,2 = 8,6 cm ; 21,7 -1,7 = 20 cm.
Volume du vase : aire du carré de base fois hauteur V = 8,6 x 8,6 x 20
=1479,2 cm3.
Volume d'une bille 4 / 3 p
r3 = 4 /3 x 3,14 x 0,93 =3,054 cm3.
Volume de 150 billes : 150 x 3,054 = 458,04 cm3.
1479,2 -458,04 ~1021 cm3 ou 1,021 L.
En ajoutant 1 L d'eau colorée, il n'y a pas de débordement.
|
|