Mathématiques,
Brevet des collèges Amérique du Sud 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Dans ce questionnaire à choix multiple, pour chaque question, une seule
proposition est exacte. Pour chacune des questions, écrire le numéro de
la question et recopier la bonne réponse. Aucune justification n’est
attendue. Une réponse correcte rapporte 1 point. Une réponse fausse ou
l’absence de réponse ne retire aucun point.
1.(4 x racine carré
2)2 = 42 x2 =32.
32 étant le PGCD de 128 et 96. (proposition 2).
2. La médiane de la
série de valeurs : 7 ; 8 ; 8 ; 12 ; 12 ; 14 ; 15 ; 15 ; 41
Médiane : 12 ; moyenne ( 7+8+8+12+12+14+15+15+41) / 9 ~ 14,67.
La médiane est inférieure à la moyenne ( proposition 2).
3. Dans une classe
de 30 élèves, les 2 /3 des élèves viennent en bus. Combien
d’élèves ne viennent pas en bus ?
30(1-2/3)=30 / 3 = 10.( proposition 3).
4.
Le système suuivant a pour solution :
2x+y=11 et x-3y = -12.
2x+y=11 et 2x-6y = -24.
Soustraire :7y=11+24 = 35 soit y = 35 /7=5
Par suite x = -12+3x5 = 3. ( proposition 3).
Exercice 2.
On considère deux
fonctions f(x) = -8x et g(x) =-6x+4.
On utilise un tableur pour calculer des images par f et g.
|
A
|
B
|
C
|
D
|
E
|
1
|
x
|
-3
|
0
|
2
|
|
2
|
f(x)=-8x
|
24
|
0
|
-16
|
-24
|
3
|
g(x)=-6x+4
|
22
|
4
|
-8
|
-14
|
1. Quelle formule peut-on saisir
dans la cellule B2 avant de la recopier vers la droite ?
= -8*B1
2. Le contenu de
la cellule E1 a été effacé. Peux-tu le retrouver ?
-24 / (-8) = 3.
3. On fabrique une
nouvelle fonction h(x)= f (x)×g (x). La fonction h est-elle une
fonction affine ?
h(x)=-8x(-6x+4)=48x2-32x.
h(x) n'est pas de la forme ax +b avec a et b constants : h(x) n'est pas
affine.
|
| ... |
|
|
Exercice 3.
Un « DJ » possède 96 titres de
musique rap et 104 titres demusique électro. Lors de
ses concerts, il choisit les titres qu’il mixe au hasard.
1. Calculer la
probabilité que le premier titre soit un titre de musique rap.
Cas favorables 96 sur un total de 200 : 96/200 = 0,48.
2. Pour varier ses
concerts, le DJ souhaite répartir tous ses titres en réalisant des «
mix » 2 identiques, c’est-à-dire comportant le même nombre de titres et
la même répartition de titres de musique « rap » et de musique «
électro ».
a. Quel est le
nombre maximum de concerts différents pourra-t-il réaliser ?
96 = 25 x3 ; 104= 23x13.
PGCD(96 ; 104) = 23=8.
b. Combien y
aura-t-il dans ce cas de titres de musique rap et de musique électro
par concert ?
96/8 =12 titres de
rap et 104 / 8 = 13 titres d'électro.
Exercice 4.
Un charpentier doit
réaliser pour un de ses clients la charpente dont il a fait un schéma
ci-dessous :
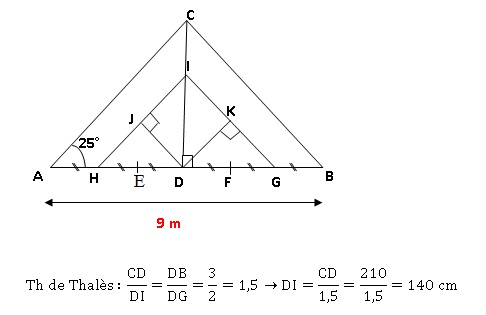
Il ne possède pas pour le moment toutes les dimensions nécessaires pour
la réaliser mais il sait que :
la charpente est symétrique par rapport à la poutre [CD],
les poutres [AC] et [HI] sont parallèles.
Vérifier les dimensions suivantes, calculées par le charpentier au
centimètre près.
Toutes les réponses doivent être justifiées.
1. Démontrer que
hauteur CD de la charpente est égale à 2,10 m.
tan 25 = CD / AD ; CD = AD tan 25 = 4,5 x tan 25 ~2,10 m.
2. Démontrer, en
utilisant la propriété de Pythagore, que la longueur AC est égale à
4,97 m.
AC2 = CD2 +AD2 =2,102 +4,52
=24,65 ; AC ~4,97 m.
3. Démontrer, en
utilisant la propriété de Thalès, que la longueur DI est égale à 1,40 m.
4.
Proposer deux méthodes différentes pour montrer que la longueur JD est
égale à 1,27 m. On ne demande pas de les rédiger mais d’expliquer la
démarche.
sin 25 = JD / HD ; JD = HD sin 25 = 3,0 x0,4226 ~1,27 m.
Calculer HI : HI2 = HD2 +ID2 = 32+1,42=10,96
; HI = 3,31 m.
Aire du triangle HID : ID x HD / 2 = IH x JD / 2 ;
JD = ID x HD / IH= 1,4 x3 / 3,31 =1,27 m.
|
|
|
|
Exercice 5.
Pour chacune des affirmations suivantes, dire si elle est vraie ou
fausse.
On rappelle que les réponses doivent être justifiées.
Affirmation 1 : n désigne un nombre entier naturel.
L’expression n2−6n +9 est toujours différente de 0. Faux.
n2−6n +9=(n-3)2 s'annule pour n = 3.
Affirmation 2 : Un faucon pèlerin vole vers sa proie à une vitesse de
180 km/h. Il est plus rapide qu’un ballon de football tiré à la vitesse
de 51m/s. Faux.
180 /3,6 =50 km/h.
Exercice 6.
Monsieur et Madame Jean vont faire construire une piscine et l’entourer
de dalles en bois sur une largeur de 2m.
Information 1
: les modèles de piscine
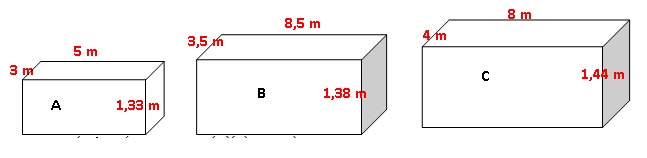
Débit de pompe : A : 8 m3 /h ; B : 10 m3 /h ; C :
12 m3/h.
Information 2
: les dalles en bois
Dalle Jécoba en bois, L 100 cm× larg. 100 cm× ép. 28 mm
Quantité pour 1m2 : 1
Epaisseur du produit (en mm) : 28
Couleur : Naturel
Prix indicatif : 13,90 € (le mètre carré)
Information 3
: la promotion sur les dalles en bois
Vente flash : 15% de remise.
Ils choisissent le modèle de piscine qui a la plus grande surface.
Quel prix payent-ils pour leurs dalles s’ils profitent de la vente
flash ?
Surface de la plus grande piscine C : S = 8 x4 = 32 m2.
Surface couverte en bois : (4+2+2) x ( 8+2+2)-32 = 64 m2.
Prix du mètre carré de bois : 13,90 x 0,85 = 11,815 €.
Coût : 11,815 x 64 = 756,16 €.
|
|
Exercice 7.
Marc veut fabriquer un bonhomme de neige en bois.
Pour cela, il achète deux boules : une boule pour la tête de rayon 3 cm
et une autre boule pour le corps dont le rayon est 2 fois plus grand.
1. a. Vérifier que
le volume de la boule pour la tête est bien 36p cm3.
4 / 3 p r3
= 4 / 3 p x33=36p cm3.
b.
En déduire le volume exact en cm3 de la boule pour le corps.
23x36p = 288 p cm3.
2. Marc coupe les
deux boules afin de les assembler pour obtenir le bonhomme de neige.
Il coupe la boule représentant la tête par un plan situé à 2 cm de son
centre.
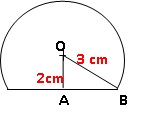
Quelle est l’aire de la surface d’assemblage de la tête et du corps ?
Arrondir le résultat au cm2.
AB2 = OB2 -OA2=9-4=5.
Aire du disque de rayon AB : p
AB2 = 3,14 x5 = 15,7 ~16 cm2.
Exercice 8.
Sophie habite Toulouse et sa meilleure amie vient de déménager à
Bordeaux. Elles décident de continuer à se voir. Sophie consulte les
tarifs de train entre les deux
villes :
- un aller-retour coûte 40 €
- si elle achète un abonnement pour une année à 442 €, un aller-retour
coûte alors moitié prix.
Aider Sophie à choisir la formule la plus avantageuse en fonction du
nombre de voyages.
Formule A : 40 x, avec x le nombre d'aller-retour.
Formule B : 442 + 20x.
Les deux formules sont identiques pôur : 40x = 442+20x ; 20 x = 442 ; x
= 442 / 20 = 22,1.
La formule A est la plus avantageuse pour un nombre d'aller-retour
inférieur ou égal à 22.
La formule B est la plus avantageuse pour un nombre d'aller-retour
supérieur à 22.
|
|