Math�matiques,
Brevet des coll�ges M�tropole septembre 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicit�s adapt�es � vos centres
d’int�r�ts.
|
|
|
|
|
|
Exercice 1.
On appelle f la fonction d�finie par f (x) = (x −1)(2x −5).
On a utilis� un tableur pour calculer les images de diff�rentes valeurs
par cette fonction f :
A2
|
f(x)
|
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
1
|
x
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
2
|
f(x)
|
5
|
0
|
-1
|
2
|
9
|
20
|
35
|
54
|
77
|
3
|
|
|
|
|
|
|
|
|
|
|
1. Pour chacune des
affirmations suivantes, indiquer si elle est vraie ou fausse.
On rappelle que les r�ponses doivent �tre justifi�es.
Affirmation 1
: f (2) = 3. Faux.
f(2) = (2-1)(2*2-5) = 1*(-1) = -1.
Affirmation 2
: L’image de 11 par la fonction f est 170. Vrai.
f(11)=(11-1)(2*11-5)=10* 17 = 170.
Affirmation 3 : La
fonction f est lin�aire. Faux.
f(x) n'est pas de la forme f(x)=ax avec a une constante.
x et f(x) ne sont pas proportionnels.
2. Une formule a
�t� saisie dans la cellule B2 puis recopi�e ensuite vers la droite.
Quelle formule a-t-on saisie dans cette cellule B2 ?
=(B1-1)*(2*B1-5)
3. Quels sont les
deux nombres x pour lesquels (x −1)(2x −5) = 0 ?
x-1 = 0 soit x = 1 et 2x-5 = 0 soit x = 2,5.
Exercice 2.
Le triangle JAB est
rectangle en A.
Les droites (MU) et (AB) sont parall�les.
Les points A,M et J sont align�s.
Les points C, U et J sont align�s.
Les points A, C et B sont align�s.
AB = 7,5 m ; MU = 3 m ; JA = 18 m.
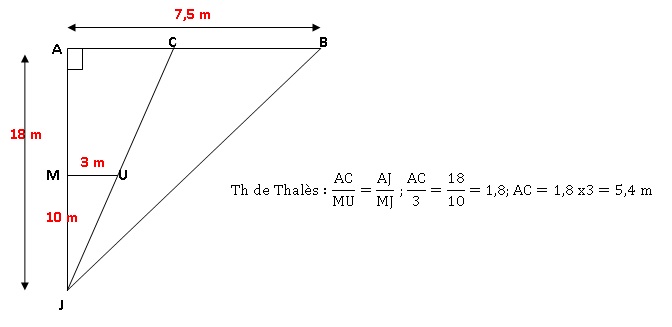
1. Calculer la
longueur JB.
JB2 = AB2 + AJ2 = 7,52+182=380,25
; JB = 19,5 m.
2. Montrer que la
longueur AC est �gale � 5,4 m.
3. Calculer l’aire
du triangle JCB.
Aire du triangle rectangle ABJ : 7,5 x18 / 2 =67,5 m2.
Aire du triangle rectangle ACJ : 5,4 x 18 / 2 = 48,6 m2.
Aire du triangle JCB : 67,5-48,6 = 18,9 m2.
|
| ... |
|
|
Exercice 3.
Principe
de fonctionnement d’un radar tron�on :
�tape 1 : enregistrement de la plaque d’immatriculation et de l’heure
de passage par
un premier portique.
�tape 2 : enregistrement de la plaque d’immatriculation et de l’heure
de passage par
un second portique.
�tape 3 : calcul de la vitesse moyenne du v�hicule entre les deux
radars par un ordinateur.
�tape 4 : calcul de la vitesse retenue afin de prendre en compte les
erreurs de pr�cisions
du radar.
�tape 5 : si la vitesse retenue est au-dessus de la vitesse limite,
l’automobiliste re�oit
une contravention.
Le pont d’Ol�ron est �quip� d’un radar tron�on sur une distance de 3,2
km.
Sur le pont, la vitesse est limit�e � 90 km/h.
1. Les deux
personnes suivantes ont re�u une contravention apr�s avoir emprunt� le
pont d’Ol�ron.
Cas 1 :
Madame Surget a �t� enregistr�e � une vitesse moyenne de 107 km/h.
Quelle est la vitesse retenue ?
On diminue la vitesse enregistr�e de 5 % : 107 x0,95 =101,65 ~102 km
/h.
Cas 2 :
Monsieur Lagarde amis 2 minutes pour parcourir la distance entre les
deux points d’enregistrement. Quelle est la vitesse retenue ?
2 min = 2 /60 = 1 /30 heure.
Vitesse enregistr�e : 3,2 x 30 = 96 km /h.
Dans ce cas, on retire 5 km/h ; vitesse retenue : 91 km /h.
2. La plaque
d’immatriculation de Monsieur Durand a �t� enregistr�e � 13 h 46 min 54
s puis � 13 h 48 min 41 s. A-t-il eu une contravention?
48 min 41 s - 46 min 54 s = 1 min 47 s =107 s.
vitesse enregistr�e : 3200 / 107 = 29,09+ m /s ou 29,09 x 3,6 = 107,7
km /h.
On retire 5 % pour obtenir la vitesse retenue : 107,7 x0,95 ~102 km/h,
donc contravention.
Exercice 4.
Trois amis se
rendent chez un apiculteur pour r�aliser quelques achats.
Le premier ach�te deux pots de miel et trois pains d’�pices pour un
montant de 24 euros.
Le deuxi�me ach�te un pot demiel et deux pains d’�pices pour unmontant
de 14,50 euros.
Le troisi�me ach�te trois pots demiel et un pain d’�pices. Combien
va-t-il payer ?
x : prix du miel et y
prix d'un pain d'�pice.
2x +3y = 24 ;
x +2y = 14,5 ou 2x +4y = 29.
Soustraire : y = 5 ; par suite x = 4,5.
Prix pay� : 3 x4,5 +5 = 18,5 €.
|
|
|
|
Exercice 5.
On consid�re le programme de calcul ci-dessous :
• Choisir un nombre.
• Soustraire 6.
• Multiplier le r�sultat obtenu par le nombre choisi.
• Ajouter 9.
1. V�rifier que
lorsque le nombre choisi est 11, le r�sultat du programme est 64.
(11-6) x 11 +9 =5 x 11 +9= 64.
2. Lorsque le
nombre choisi est −4, quel est le r�sultat du programme ?
(-4-11)(-4) +9 = (-15)(-4) +9 = 60+9 = 69.
3. Th�o affirme
que, quel que soit le nombre choisi au d�part, le r�sultat du programme
est toujours un nombre positif. A-t-il raison ?
Oui : (n-6)x n +9 = n2-6x +9 = (n-3)2. Un carr�
est toujours positif ou nul.
Exercice 6.
Louise a t�l�charg� une liste de lecture sur son lecteur MP4 :
:
Titre
|
Nom
de l'interpr�te
|
Dur�e
de la chanson (s)
|
Mamat�ou
|
Timat�
|
232
|
La
diff�rence
|
Timat�
|
211
|
Amazing
|
Timat�
|
214
|
Tes
racines
|
Timat�
|
175
|
YoungBov
|
Hudad
|
336
|
La
ficelle
|
Maen
|
191
|
Fou
fou fou
|
Maen
|
184
|
Nina
|
Maen
|
217
|
1. a. Quelle est la
dur�e totale de cette liste ? Exprimer cette dur�e en minutes et
secondes.
1760 s ou 29 min 20 s.
b. D�terminer le
pourcentage de chansons dont la dur�e est sup�rieure � 3 min 30 s.
3 min 30 = 180 +30 = 210 s.
5 chansons sur 8 soit 5 / 8 x100 = 62,5 %.
2. Louise d�cide
d’utiliser la fonction � al�atoire � de son MP4. Cette fonction choisit
au hasard une chanson parmi celles qui sont pr�sentes dans la liste de
lecture. Chaque chanson a la m�me probabilit� d’�tre �cout�e.
D�terminer la probabilit� que Louise �coute une chanson de Maen.
3 cas favorables sur 8 soit une probabilit� de 3 / 8=0,375..
3. Elle r�p�te 25
fois l’utilisation de la fonction � al�atoire � de son MP4 et note �
chaque fois le nomde l’interpr�te qu’elle a �cout�. Les r�sultats
qu’elle obtient sont not�s dans le graphique ci-dessous. D�terminer la
fr�quence d’�coute de Hudad.
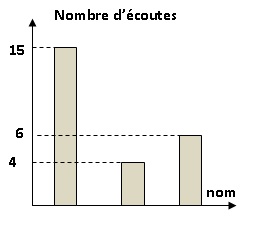
4 / 25 = 0,16.
|
|
Exercice 7.
Une
boulangerie veut installer une rampe d’acc�s pour des personnes �
mobilit� r�duite. Le seuil de la porte est situ� � 6 cm du sol.
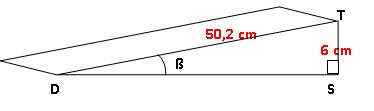
La norme impose que la rampe d’acc�s forme un angle inf�rieur � 3� avec
l’horizontale sauf dans certains cas.
Cas particuliers :
L’angle form� par la rampe avec l’horizontale peut aller :
- jusqu’� 5� si la longueur de l’horizontale est inf�rieure � 2 m.
- jusqu’� 7� si la longueur de l’horizontale est inf�rieure � 0,5 m.
Cette rampe est-elle conforme � la norme ?
sin � =TS / DT =6 / 50,2 =0,1195 ; � = 6,87 �.
Longueur DS : DS2 = DT2 -TS2 = 50,22-62=23484,04
; DS = 49,84 cm, valeur inf�rieure � 0,5 m.
La rampe est conforme.
|
|
