Mathématiques,
Brevet des collèges Métropole 2015
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Une coopérative collecte le lait dans différentes exploitations
agricoles.
Le détail, de la collecte du jour ont été saisis dans une feuille de
calcul d’un tableur.
|
A
|
B
|
1
|
Exploitation
agricole
|
Quantité
de lait collecté ( L)
|
2
|
Beauséjour
|
1250
|
3
|
Le
verger
|
2130
|
4
|
La
fourragère
|
1070
|
5
|
Petit
pas
|
2260
|
6
|
La
Chausse pierre
|
1600
|
7
|
Le
Palet
|
1740
|
8
|
Quantité
totale de lait collecté
|
|
1. Une
formule doit être saisie dans la cellule B8 pour obtenir la quantité
totale de lait collecté. Parmi les quatre propositions ci-dessous,
recopier celle qui convient.
SOMME(B2 : B7) ; SOMME(B2 : B8) ; =SOMME(B2 : B7) ; =SOMME(B2 : B8)
2. Calculer la
moyenne des quantités de lait collecté dans ces exploitations.
S =(1250 +2130+1070 +2260 +1600 +1740 ) / 6=1675 L
3. Quel pourcentage
de la collecte provient de l’exploitation « Petit Pas » ? On arrondira
le résultat à l’unité.
2260 / S x 100= 2260 / 10050 x100 =22,48 ~22 %.
Exercice 2.
Voici un programme de calcul sur lequel travaillent quatre élèves.
• Prendre un nombre
• Lui ajouter 8
• Multiplier le résultat par 3
• Enlever 24
• Enlever le nombre de départ
Voici ce qu’ils affirment :
Sophie : «Quand je prends 4 comme nombre de départ, j’obtiens, 8 »
Martin : « En appliquant le programme à 0, je trouve 0. »
Gabriel : «Moi,j’ai pris −3 au départ et j’ai obtenu −9. »
Faïza : « Pour n’importe quel nombre choisi, le résultat final est égal
au double du nombre de départ. »
Pour chacun de ces quatre élèves expliquer s’il a raison ou tort.
Soit x le nombre choisi :
x+8 ; (x+8) x3 ; (x+8) x3 -24 ; (x+8) x3 -24 -x = 2x.
Sophie, Martin, Faîza ont raison ; Gabriel a tord.
|
| ... |
|
|
Exercice 3.
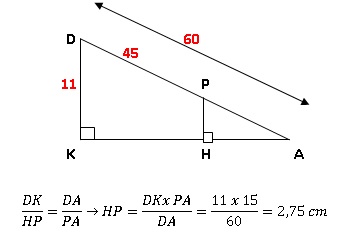
Dans la figure ci-dessous, qui n’est pas à l’échelle
:
• les pointsD, P et A sont alignés ;
• les points K, H et A sont alignés
DA = 60 cm ; DK = 11 cm ; DP = 45 cm.
1. Calculer KA au
millimètre près.
KA2 = AD2 -DK2 = 602-112
=3479 ; KA =58,98 cm ~59,0 cm.
2. Calculer HP.
Exercice 4.
1. On considère la
fonction f définie par f (x) = −6x +7.
Déterminer l’image de 3 par la fonction f .
f(3) = -6 x3 +7 = -11.
2. Arthur a le
choix pour s’habiller aujourd’hui entre trois chemisettes (une verte,
une bleue et une rouge) et deux shorts (un vert et un bleu). Il décide
de s’habiller en choisissent au hasard une chemisette puis un short.
Quelle est la probabilité qu’Arthur soit habillé uniquement en vert ?
Probabilité d'une chemisette verte : 1/3 ; probabilité d'un short vert
: 1 / 2.
Probabilité d'être habillé tout en vert : 1 /3 x 1/2 = 1 /6.
3. Ariane affirme
que 240 est le double de 239. A-t-elle raison ?
Oui : 240 = 2 x 239.
4. Loïc affirme
que le PGCD d’un nombre pair et d’un nombre impair est toujours égal à
1.
A-t-il raison ?
Non : le PGCD de 12 et de 21 est égal à 3
5. Résoudre
l’équation : 5x −2 = 3x +7.
5x-3x=7+2 ; 2x = 9 ; x = 4,5.
|
|
|
|
Exercice 5.
Agnês envisage de peindre la façade de son hangar. Une seule couche de
peinture suffit.
Renseignements concernant un pot de peinture
Volume : 6 L ; temps de séchage : 8 h ; surface couverte : 24 m2
; prix : 103,45 €.
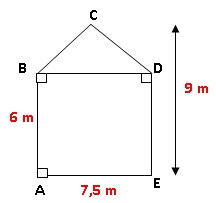
1. Quel est le
montant minimum à prévoir pour l’ achat des pots de peinture ?
Aire du rectangl : 6 x7,5 = 45 m2.
Aire du triangle de hauteur égale à 3 m : 7,5 x3 / 2 =11,25 m2.
Aire de la façade : 45 +11,25 = 56,25 m2.
Il faut prévoir 3 pots de peinture.
Coût : 3 x103,45 = 310,35 €.
2. Agnès achète la
peinture et tout le matériel dont elle a besoin pour ses travaux.
Le montant total de la facture est de 343,50 €.
Le magasin lui propose de régler 2 /5 de la facture aujourd’hui et le
reste en trois mensualités identiques.
Quel sera le montant de chaque mensualité ?
Montant des trois mensualités : 343,50 -343,5 x2 /5 = 343,50 x3 / 5 =
206,1 €
Montant d'une mensualité : 206,1 / 3 = 68,7 €.
Exercice 6.
La distance parcourue par un véhicule entre le moment où le conducteur
voit un obstacle et l’arrêt complet du véhicule est égale à la
distance de réaction ( distance parcourue entre l’instant où le
conducteur voit l’obstacle et celui où il commence à freiner ( ajoutée
à la distance de freinage ( distance parcourue depuis le début du
freinage jusqu’à l’arrêt du véhicule ).
Distance d’arrêt = distance de réaction + distance de freinage
1. Un scooter
roulant à 45 km/h freine en urgence pour éviter un obstacle. À cette
vitesse, la distance de réaction est égale à 12,5 m et la distance de
freinage à 10m. Quelle est la distance d’arrêt ?
12,5 + 10 = 22,5 m.
2. Les deux
graphiques suivants représentent, dans des conditions normales et sur
route sèche, la distance de réaction et la distance de freinage en
fonction de la vitesse du véhicule. En utilisant ces graphiques,
répondre aux questions suivantes :
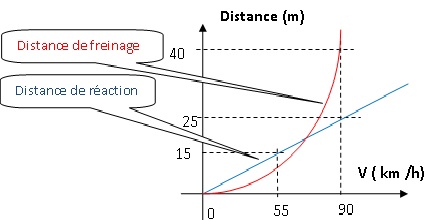
a. La distance de
réaction est de 15 m. À quelle vitesse roule-t-on ? 55 km /h.
b. La distance de
freinage du conducteur est-elle proportionnelle à la vitesse de son
véhicule ?
Non, la courbe rouge n'est pas une droite passant par l'origine.
c. Déterminer la
distance d’arrêt pour une voiture roulant à 90 km/h.
40 +25 = 65 m.
3. La distance de
freinage en mètres, d’un véhicule sur route mouillée, peut se calculer
à l’aide de la formule sui vante, où v est la. vitesse en km/h du
véhicule : v2 / 152,4.
Calculer au mètre près la distance de freinage sur routemouillée à 110
km/h.
1102 / 152,4 ~79 m.
|
|
Exercice 7.
Une descente dont la pente est de 10% signifie que pour un déplacement
horizontal de 100 mètres, le dénivelé est de 10 mètres.
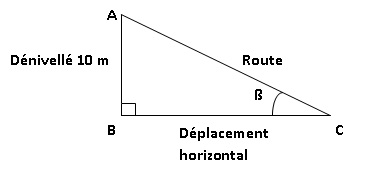
1. Déterminer la mesure de l’angle �BCA que fait
la route avec l’horizontale. Arrondir la réponse au degré.
tan ß = 10 / 100 = 0,10 ; ß = 5,70 ~ 6 °.
2. Dans certains
pays, il arrive parfois que la pente d’une route ne soit pas donnée par
un pourcentage,mais par une indication telle que « 1 : 5 », ce qui veut
alors dire que pour un déplacement horizontal de 5 mètres, le dénivelé
est de 1 mètre.
Lequel des deux indications ci-dessous indique la pente la plus forte ?
15 % : dénivellé de 15 m pour un déplacement horizontal de 100 m
ou encore dénivellé de 15 / 20 =0,75 m pour un déplacement horizontal
de 5 m.
1 : 5 : dénivellé de 1 m pour un déplacement horizontal de 5 m ; cette
indication indique la plus grande pente..
|
|