Mathématiques, Brevet des collèges Métropole septembre 2014

Mathématiques, Brevet des collèges Métropole septembre 2014

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Exercice 1.
Cédric s’entraîne pour l’épreuve de vélo d’un triathlon.
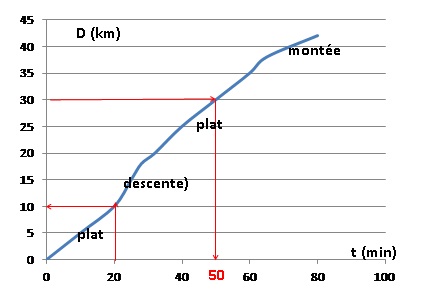
La courbe ci-dessous représente la distance en kilomètres en fonction du temps écoulé en minutes
Pour les trois premières questions, les réponses seront données grâce à des lectures
graphiques. Aucune justification n’est attendue sur la copie.
1. Quelle distance Cédric a-t-il parcourue au bout de 20 minutes ? 10 km
2. Combien de temps amis Cédric pour faire les 30 premiers kilomètres ? 50 minutes
3. Le circuit de Cédric comprend une montée, une descente et deux portions plates. Reconstituer dans l’ordre le trajet parcouru par Cédric.
En descente la vitesse augmente, pente du graphe plus grande que celle du plat..
En montée, la vitesse diminue, pente plus faible que celle du plat.

4. Calculer la vitesse moyenne de Cédric (exprimée en km/h) sur la première des quatre parties du trajet.
10 km parcourus en 20 minutes soit 1 / 3 heure.
v = 10 x3 = 30 km /h.

.
.

Exercice 2.
Dans cet exercice, les figures codées ne sont pas en vraie grandeur.
Affirmation 1 : Le volume du solide (1) est 56 cm³. Faux.

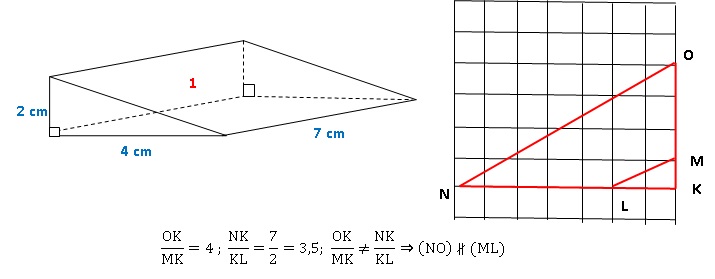
Aire de base triangulaire fois hauteur = 2 x4 / 2 x7 = 28 cm³.
Affirmation 2 : Les droites (ML) et (NO) sont parallèles. Faux.
Affirmation 3 : La diagonale d’un carré d’aire 36 cm² a pour longueur 6 racine carrée(2) cm. Vrai.
côté du carré : racine carrée (36) = 6 ; diagonale = côté fois racine carrée (2).
Affirmation 4 : 0 a un seul antécédent par la fonction qui à tout nombre x associe 3x +5. Vrai.
0 = 3x+5 , 3x = -5 ; x = -5 /3.

Exercice 3.
Dans une classe de collège, après la visite médicale, on a dressé le tableau suivant :

Porte des lunettes
Ne porte pas de lunettes

Fille
3
15

Garçon
7
5

Les fiches individuelles de renseignements tombent par terre et s’éparpillent.
1. Si l’infirmière en ramasse une au hasard, quelle est la probabilité que cette fiche soit :
a. celle d’une fille qui porte des lunettes ?
3 cas favorables sur 30 ; la probabilité qu'une fille porte des lunettes est : 3 / 30 = 0,10.
b. celle d’un garçon ?
12 cas favorables sur 30 ; probabilité que ce soit un garàon : 12 / 30 = 2 / 5 = 0,40.
2. Les élèves qui portent des lunettes dans cette classe représentent 12,5% de ceux qui en portent dans tout le le collège. Combien y a-t-il d’élèves qui portent des lunettes dans le collège ?
10 élèves portent des lunettes dans la classe.
10 /0,125 = 80 élèves portent des lunettes dans le collège.

Exercice 4.
On s’intéresse à la zone au sol qui est éclairée la nuit par deux sources de lumière : le lampadaire de la rue et le spot fixé en F sur la façade de l’immeuble.

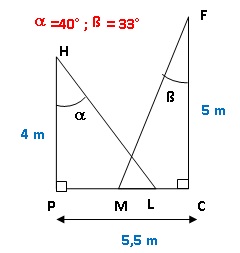
1. Justifier que l’arrondi au décimètre de la longueur PL est égal à 3,4 m.
tan a = PL / PH ; PL =PH tan a =4 tan 40 ~3,36 ~ 3,4 m.
2. Calculer la longueur LM correspondant à la zone éclairée par les deux sources de lumière. On arrondira la réponse au décimètre.
tan b = MC / FC ; MC =FC tan ß =5 tan 33 ~ 3,25 m.
PL +MC -ML= PC ; ML = PL+MC-PC =3,36 +3,25 -5,5 =1,11 ~1,1 m.
3. On effectue des réglages du spot situé en F afin que M et L soient confondus.
Déterminer la mesure de l’angle� CFM. On arrondira la réponse au degré.
tan ß' = LC / FC =(5,5-3,4) / 5 = 0,42 ; ß' ~22,8°~23°.

.
.

Exercice 5.
Léa pense qu’en multipliant deux nombres impairs consécutifs (c’est-à-dire qui se suivent) et en ajoutant 1, le résultat obtenu est toujours un multiple de 4.
1. Étude d’un exemple :
5 et 7 sont deux nombres impairs consécutifs.
a. Calculer 5×7+1.
5 x7 = 35 ; 35+1 = 36.
b. Léa a-t-elle raison pour cet exemple ?
Léa a raison pour cet exemple.
2. Le tableau ci-dessous montre le travail qu’elle a réalisé dans une feuille de calcul.

A
B
C
D
E

1

Nombre impair
Nombre impair suivant
Produit de ces nombres
impairs consécutif
Résultat

2
x
2x+1
2x+3
(2x+1)(2x+3)
(2x+1)(2x+3)+1

3
0
1
3
3
4

4
1
3
5
15
16

5
2
5
7
35
36

6
3
7
9
63
64

7
4
9
11
99
100

8
5
11
13
143
144

a. D’après ce tableau, quel résultat obtient-on en prenant comme premier nombre impair 17 ?
17 x19 +1 = 324
b. Montrer que cet entier est un multiple de 4.
324 / 4 =81.
c. Parmi les quatre formules de calcul tableur suivantes, deux formules ont pu être saisies dans la cellule D3. Lesquelles ? Aucune justification n’est
attendue.
Formule 1 : =(2*A3+1)*(2*A3+3)
Formule 2 : = (2*B3 + 1)*(2*C3 + 3)
Formule 3 : = B3*C3
Formule 4 : = (2*D3+1)*(2*D3+3).
3. Étude algébrique :
a. Développer et réduire l’expression (2x +1)(2x +3)+1.
4x²+2x+6x+3+1 =4x²+8x+4.
b. Montrer que Léa avait raison : le résultat obtenu est toujours un multiple de 4.
4x²+8x+4 = 4 (x² +2x+1) = 4 (2x+1)².

Exercice 6.
Julien veut mesurer un jeune chêne avec une croix de bûcheron comme le montre le schéma ci-dessous.
Il place la croix de sorte que O, D et A d’une part et O, E et B d’autre part soient alignés.
Il sait que DE = 20 cm et OF = 35 cm. Il place [DE] verticalement et [OF] horizontalement. Il mesure au sol BC = 7,7 m.

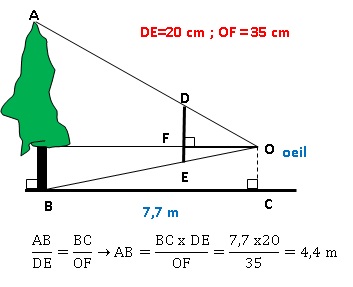
1. Le triangle ABO est un agrandissement du triangle ODE. Justifier que le coefficient d’agrandissement est 22.
BC / OF = 7,7 / 0,35 = 22.
2. Calculer la hauteur de l’arbre en mètres.
3. Certaines croix du bûcheron sont telles que DE = OF. Quel avantage apporte ce type de croix ?
La mesure au sol OF donne directement la hauteur de l'arbre.
4. Julien enroule une corde autour du tronc de l’arbre à 1,5 m du sol. Il mesure ainsi une circonférence de 138 cm.
Quel est le diamètre de cet arbre à cette hauteur ? Donner un arrondi au centimètre près.
pD = 138 ; D = 138 /3,14 = 43,9 ~44 cm.

Exercice 7.
Pour préparer un séjour d’une semaine à Naples, un couple habitant Nantes a constaté que le tarif des billets d’avion aller-retour Nantes-Naples était beaucoup plus élevé que celui des billets Paris-Naples. Il étudie donc quel serait le coût d’un trajet aller retour Nantes-Paris pour savoir s’il doit effectuer son voyage en avion à partir de Nantes ou à partir de Paris.
Voici les informations que ce couple a relevées :
Vol aller-retour au départ de Nantes
Départ de Nantes le 23/11/2014 : 06 h 35 ; Arrivée à Naples le 23/11/2014 : 09 h 50
Départ de Naples le 30/1112014 : 12 h 50 ; Arrivée à Nantes le 30/1112014 : 16 h 25
Prix par personne du vol aller-retour : 530 €.
Vol aller-retour au départ de Paris
Départ de Paris le 23/11/2014 : 11 h 55 ; Arrivée à Naples le 23/11/2014 : 14 h 10
Départ de Naples le 30/11/2014 : 13 h 10 ; Arrivée à Paris le 30/11/2014 : 15 h 30
Prix par personne du vol aller-retour : 350 €.
Les passagers doivent être présents 2 heures avant le décollage pour procéder à l’embarquement.

Prix et horaires des trains pour un passager
Trajet Nantes - Paris (Aéroport) 23 novembre
Départ 06 h22 . Prix 51,00 €. Durée 03 h 16 direct. Voyagez avec TGV
Trajet Paris (Aéroport) - Nantes 30 novembre
Départ 18 h 20. Prix 42,00 €. Durée 03 h 19 direct.Voyagez avec TGV .

Trajet en voiture : Parking de l’aéroport de Paris. Tarif : 58 € pour une semaine.
Consommation moyenne : 6 litres aux 100 km.
Péage Nantes-Paris : 35,90 €. Distance domicile-aéroport de Paris : 409 km.
Carburant : 1,30 € par litre.Temps estimé : 4 h 24 min.
1. Expliquer pourquoi la différence entre les prix des 2 billets d’avion s’élève à 360 ( pour ce couple)
2 x (530-350)=360.
2. Si le couple prend la voiture pour aller à l’aéroport de Paris :
a. Déterminer l’heure avant laquelle il doit partir de Nantes.
4 h 24 + 2h = 6 h24.
Heure du décollage : 11 h 55.
Heure de départ en voiture : 11 h 55 -6 h 24 = 5 h 31 min.
b. Montrer que le coût du carburant pour cet aller est de 31,90 €.
Consommation : 409 /100 x6 =24,54 L.
Prix du carburant : 24,54 x1,30 = 31,90 €.
3. Quelle est l’organisation de voyage la plus économique ?
Voiture. Prix du carburant + péage aller retour : 2(31,90 +35,9) = 135,6 €.
Parking Paris : 58 €. Total 135,6 +58 = 193,6 €.
Trains : 2(51 +42) =186 €.
Prendre le train entre Nantes et Paris, puis l'avion de Paris à Naples.

menu