Mathématiques, Brevet des collèges Asie 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Exercice 1.  QCM On laisse tomber une balle d’une hauteur de 1 mètre. A chaque rebond elle rebondit des 3 /4 de la hauteur d’où elle est tombée. Quelle hauteur atteint la balle au cinquième rebond ? Arrondir au cm près. Après le premier rebond, la hauteur atteinte est 0,75 m= 75 cm. Après le second rebond, la hauteur atteinte est 0,75 x0,75=0,5625 m~ 56 cm. Après le troisième rebond, la hauteur atteinte est 0,5625 x0,75=0,421875 m~ 42 cm. Après le quatrième rebond, la hauteur atteinte est 0,421875 x0,75=0,31640 m~ 32 cm. Après le cinquième rebond, la hauteur atteinte est 0,31640 x0,75=0,237 m~ 24 cm. . . Exercice 2. Une corde de guitare est soumise à une tension T, exprimée en Newton (N), qui permet d’obtenir un son quand la corde est pincée. Ce son plus ou moins aigu est caractérisé par une fréquence f exprimée en Hertz (Hz). La fonction qui à une tension T associe sa fréquence est définie par la relation : f (T ) = 20 racine carrée (T) . 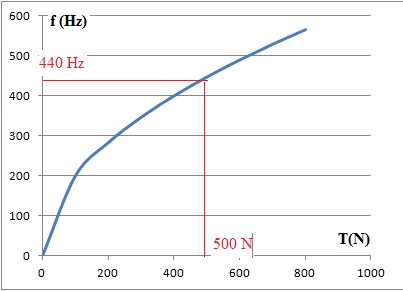On donne ci-dessous la représentation graphique de cette fonction. Déterminer graphiquement une valeur approchée de la tension à appliquer sur la corde pour obtenir un « La3 », f = 440 Hz. Déterminer par le calcul la note obtenue si on pince la corde avec une tension de 220 N environ. f = 20 racine carrée (220) ~297 Hz.  La corde est un Ré3. La corde casse lorsque la tension est supérieure à 900 N. Quelle fréquence maximale peut-elle émettre avant de casser ? f = 20 racine carrée (900) =600 Hz. Exercice 3. 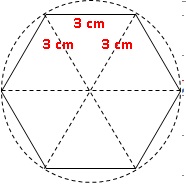Les alvéoles des nids d’abeilles présentent une ouverture ayant la forme d’un hexagone régulier de côté 3 mm environ. Construire un agrandissement de cet hexagone de rapport 10. (aucune justification de la construction n’est attendue). Exercice 4. Dans chaque cas, dire si l’affirmation est vraie ou fausse. Justifier. Cas 1 : À l’entrée d’un cinéma, on peut lire les tarifs ci-dessous pour une place de cinéma. Tarif d’une place de cinéma : Plein tarif : 9,50 € Enfants (−12 ans) : 5,20 € Étudiants : 6,65 € Séniors : 7,40 € Affirmation 1 : Les étudiants bénéficient d’une réduction de 30% sur le plein tarif. Vrai. (9,5 -6,65) /9,50=0,3 ( 30 %). Cas 2 : a et b désignent des entiers positifs avec a > b. Faux. Affirmation 2 : PGCD(a ; b) = a −b. Contre exemple : a = 5 et b = 3. Le PGCD(5 ; 3) = 1 et non pas 5-3=2. Cas 3 : A est égale au produit de la somme de x et de 5 par la différence entre 2x et 1. x désigne un nombre relatif. Affirmation 3 : A = 2x2 +9x −5. Vrai. Somme de x et de 5 : (x+5). Différence entre 2x et 1 :(2x-1). (x+5)(2x-1)=2x2 +10x-x-5 = 2x2+9x-5. . . Exercice 5. En utilisant le codage et les données, dans chacune des figures, est-il vrai que les droites (AB) et (CD) sont parallèles ? Justifier vos affirmations. 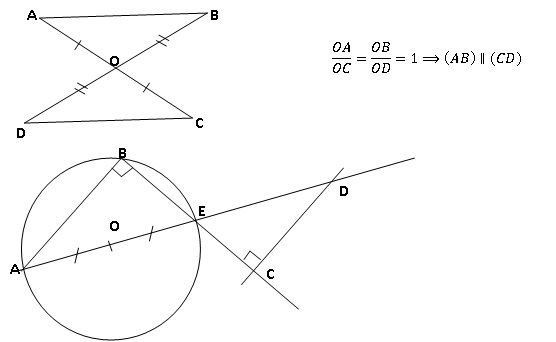Le triangle ABE, inscrit dans un demi-cercle est rectangle en B. Les droites (AB) et (CD), perpendiculaires à une même troisième ( BC), sont donc parallèles. Exercice 6. Une association décide d’organiser une tombola pour financer entièrement une sortie pour ses adhérents d’un montant de 2 660 €. Le 1er ticket tiré au sort fera remporter le gros lot d’une valeur de 300 €, Les 10 tickets suivants tirés au sort feront remporter un lot d’une valeur de 25 € chacun. Les 20 tickets suivants tirés au sort feront remporter un lot d’une valeur de 5 € chacun. L’association finance entièrement les lots. Chaque ticket de tombola est vendu 2 € et les tickets sont vendus durant 6 jours. 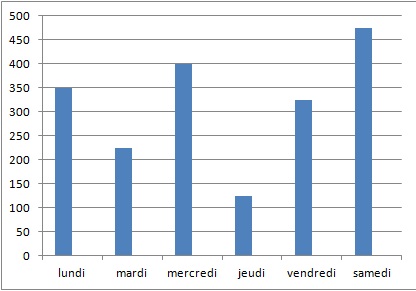On a représenté ci-dessous le diagramme des ventes des tickets durant ces 6 jours. 1. L’association pourra-t-elle financer entièrement cette sortie ? Recettes : (350 +225 +400 +125 +325 +475) x2=1900 x2 = 3800 €. Valeur des lots : 300 +25 x 10 +20 x5 = 650 €. Bénéfice : 3800 -650 = 3150 €, valeur supérieure à 2660 €, la sortie est donc financée. 2. Pour le même nombre de tickets vendus, proposer un prix de ticket de tombola permettant de financer un voyage d’une valeur de 10 000 € ? Quel serait le prix minimal ? 1900 x = (10 000+650) ; x = 10 650 / 1900 =5,61 € 3. Le gros lot a été déjà tiré. Quelle est la probabilité de tirer un autre ticket gagnant ? (donner le résultat sous la forme fractionnaire) 30 tickets gagnants sut 1900-1 = 1899. La probabilité  de tirer un ticket gagnant est : 30 /1899 ~ 0,016. Exercice 7. Les gérants d’un centre commercial ont construit un parking souterrain et souhaitent installer un trottoir roulant pour accéder de ce parking au centre commercial. Les personnes empruntant ce trottoir roulant ne doivent pas mettre plus de 1 minute pour accéder au centre commercial. La situation est présentée par le schéma ci-dessous. Modèle 1: • Angle d’inclinaison maximum avec l’horizontale : 12 °. • Vitesse : 0,5 m/s Modèle 2 :• Angle d’inclinaison maximum avec l’horizontale : 6 °.  • Vitesse : 0,75 m/s. Est-ce que l’un de ces deux modèles peut convenir pour équiper ce centre commercial ? Justifier. PC2 = CH2 +PH2 = 32+252=9+625=634 ; PC ~25,2 m. Durée du parcours PC sur le trotoir : modèle 1 : 25,2 /0,5 =50,4 s. Le modèle 1 convient. Le modèle 2 ne convient pas, la pente est supérieure à 6°.

menu