Mathématiques,
Brevet des collèges Amérique du Nord 2013
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
1. L’arbre
ci-dessous est un arbre de probabilité. La probabilité manquante est :
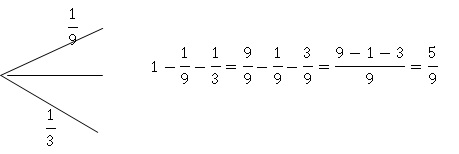
2.
Dans une salle, il y a des tables à 3 pieds et à 4 pieds. Léa compte
avec les yeux bandés 169 pieds. Son frère lui indique qu’il y a 34
tables à 4 pieds. Sans enlever son bandeau, elle parvient à donner le
nombre de tables à 3 pieds qui est de :.
On note y le nombre de tables à 3 pieds.
34 x4 +3y=169 ; 3y =33 ; y =11.
3. 90% du volume
d’un iceberg est situé sous la surface de l’eau.
La hauteur totale d’un iceberg dont la partie visible est 35 m est
d’environ :
35 m correspond au dixième de la hauteur totale ; Htotale =
35 x10 =350 m.
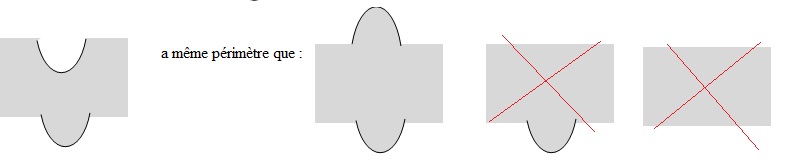
4. 
Exercice 2.
Arthur vide sa tirelire et constate qu’il possède 21
billets.
Il a des billets de 5 € et des billets de 10 € pour une somme totale de
125 €.
Combien de billets de chaque sorte possède-t-il ?
On note x le nombre de billets de 5 € ;
21-x représente le nombre de billets de 10 €.
5 x + (21-x)10 =125 ;
5x+210-10x =125 ;
5x = 85 ; x = 17.
17 billets de 5 € et 4 billets de 10 €.
|
|
|
Exercice 3.
Caroline souhaite s’équiper pour faire du roller.
Elle a le choix entre une paire de rollers gris à 87 € et une paire de
rollers noirs à 99 €.
Elle doit aussi acheter un casque et hésite entre trois modèles qui
coûtent respectivement 45 €, 22 € et 29 €.
1. Si elle choisit
son équipement (un casque et une paire de rollers) au hasard, quelle
est la probabilité pour que l’ensemble lui coûte moins de 130 € ?
Nombre de cas possibles : 6.
Nombre de cas favorables : rollers gris 87 € et casque à 22 € ou 29 € ;
rollers noir et casque à 22
€ ou 29 € ;
Probabilité de dépenser moins de 130 € : 4 / 6 = 2 / 3 ~0,67.
2. Elle
s’aperçoit qu’en achetant la paire de rollers noirs et le casque à 45
€, elle bénéficie d’une réduction de 20% sur l’ensemble.
a. Calculer le prix
en euros et centimes de cet ensemble après réduction.
(99 + 45) x0,80 = 115,2 €
b. Cela
modifie-t-il la probabilité obtenue à la question 1 ? Justifier la
réponse.
Oui, car il y a un cas favorable supplémentaire et la probabilité
devient 5 / 6 ~0,83
.
Exercice 4.
Flavien veut répartir la totalité de 760 dragées au chocolat et 1 045
dragées aux amandes dans des sachets dans des sachets ayant la même
répartition de dragées au chocolat et aux amandes.
1. Peut-il faire 76
sachets ? Justifier la réponse.
Non, car 76 est un diviseur de 760 mais pas un divisuer de 1045.
2. a. Quel nombre
maximal de sachets peut-il réaliser ?
1045=5 x11 x19 ; 760 = 23 x5x19 ; le PGCD de 760 et 1045 est
égal à 5 x19 =95.
b. Combien de
dragées de chaque sorte y aura-t-il dans chaque sachet ?
760 / 95=8 dragées
au chocolat et 1045 / 95 =11 dragées aux amandes.
|
|
|
|
Exercice 5.
Tom doit
calculer 3,52.
« Pas la peine de prendre la calculatrice », lui dit Julie, tu n’as
qu’à effectuer le produit de 3 par 4 et rajouter 0,25.
1. Effectuer le
calcul proposé par Julie et vérifier que le résultat obtenu est bien le
carré de 3,5.
3 x4 +0,25 = 12,25 ; 3,52 = 12,25.
2. Proposer une
façon simple de calculer 7,52 et donner le résultat.
(8-0,5)(7+0,5) = 8x7 -0,25+8 x0,5-7 x0,5 =8 x7 +0,25 = 56+0,25 =56,25.
3. Julie propose la
conjecture suivante : (n +0,5)2= n(n +1)+0,25
n est un nombre entier positif.
Prouver que la conjecture de Julie est vraie (quel que soit le nombre
n).
(n +0,5)2=
n2 +n+0,25 =n (n+1) +0,25.
La conjecture
est vraie.
Exercice 6.
On dispose d’un carré de métal de 40
cm de côté. Pour fabriquer une boîte parallélépipèdique, on enlève à
chaque coin un carré de côté x et on relève les bords par pliage.
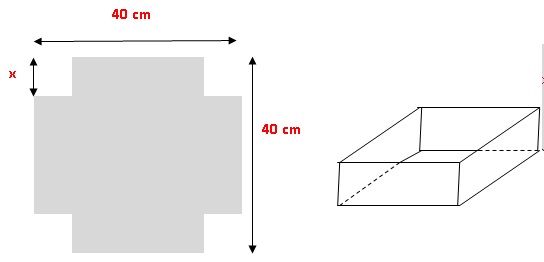
1. Quelles sont les
valeurs possibles de x ?
On enlève 2x à 40 cm. x doit être compris entre 0 et 20 cm. [0 ; 20 cm
].
2. On donne x = 5
cm. Calculez le volume de la boîte.
aire du carré de base x hauteur = 30 x 30 x5 =4,5 103 cm3.
3. Le graphique
suivant donne le volume de la boîte en fonction de la longueur x..
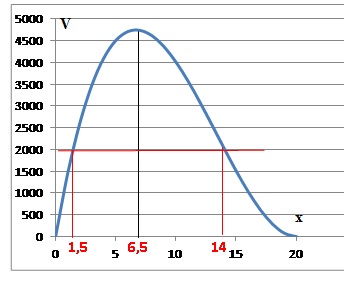
On répondra aux questions à l’aide du graphique.
a. Pour quelle
valeur de x, le volume de la boîte est-il maximum ? 6,5 cm
b. On souhaite que
le volume de la boîte soit 2 000 cm3. Quelles sont les
valeurs possibles de x ?
1,5 cm et 14 cm.
|
|
Exercice 7.
Le
Pentagone est un bâtiment hébergeant le ministère de la défense des
Etats-Unis. Il a la forme d’un pentagone régulier inscrit dans un
cercle de rayon OA= 238 m.
Il est représenté par le schéma suivant :.
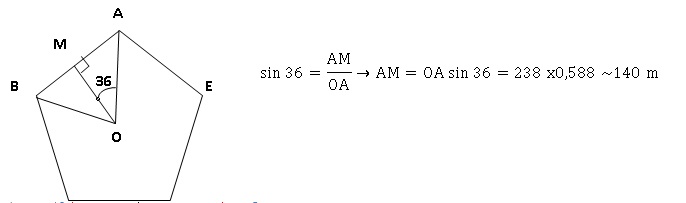
1. Calculer la
mesure de l’angle �AOB.
360 / 5=72°.
2. La hauteur issue
de O dans le triangle AOB coupe le côté [AB] au point M.
a. Justifier que
(OM) est aussi la bissectrice de �AOB et la médiatrice de [AB].
Le triangle AOB est isocèle en O ( OA = OB = rayon du cercle de centre
O).
La hauteur issue du sommet d'un triangle isocèle est également
médiatrice de la base AB et bissectrice de l'angle AOB.
b. Prouver que [AM]
mesure environ 140 m.
c. En déduire une
valeur approchée du périmètre du Pentagone
140 x10 =1400 m.
Exercice 8.
Les longueurs sont données en centimètres. ABCD est
un trapèze.
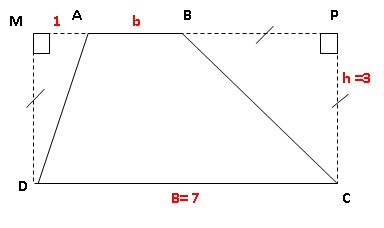
1. a. Donner une
méthode permettant de calculer l’aire du trapèze ABCD.
b. Calculer l’aire
de ABCD.
aire du rectangle CDMP - aire du triangle rec tangleAMD-aire du
triangle rectangle isocèle BCP.
B x h -AM x h / 2 -BP x h / 2.
[B-0,5 (AM +BP) ] h = [ 7-0,5(1+3) ] x3 = 15 cm2.
2. L’aire d’un
trapèze A est donnée par l’une des formules suivantes. Retrouver la
formule juste en expliquant votre choix.
B-0,5 (AM +BP) = 0,5 [2B- (AM +BP] = 0,5 [B +B-AM-BP] = 0,5 [B +b] ;
Aire = 0,5 [B +b] h.
.
|
|