Mathématiques,
Brevet des collèges Pondichéry 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Quatre affirmations sont données ci-dessous.
1. L'expression suivante est un nombre entier. Vrai.
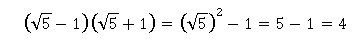
2. 4 n'admet que deux diviseurs. Faux.
1, 2, 4 divisent 4..
3. Un cube, une pyramide à base carrée et un pavé droit totalisent 17 faces. Vrai.
6 pour le cube +5 pour la pyramide à base carrée + 6 pour le pavé droit.
4. Les droites (AB) et (CD) sont parallèles.
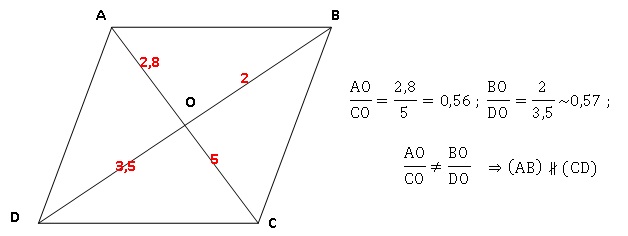
Exercice 2.
Un professeur de SVT demande aux 29 élèves d’une classe de sixième de faire germer
des graines de blé chez eux. Le professeur donne un protocole expérimental à suivre :
- mettre en culture sur du coton dans une boîte placée dans une pièce éclairée, de température entre 20 ° et 25 °C;
- arroser une fois par jour ;
- il est possible de couvrir les graines avec un film transparent pour éviter l’évaporation
de l’eau.
Le tableau ci-dessous donne les tailles des plantules (petites plantes) des 29 élèves à
10 jours après la mise en germination.
Taille en cm
|
0
|
8
|
12
| 14
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
| Effectif |
1
|
2
|
2
| 4
|
2
|
2
|
3
|
3
|
4
|
4
|
2
|
1. Combien de plantules ont une taille qui mesure au plus 12 cm ? 5.
2. Donner l’étendue de cette série.
Plus grande valeur - plus petite valeur = 22-0=22.
3. Calculer la moyenne de cette série. Arrondir au dixième près.
(8 x2 +12 x2+14 x4 +16 x2+17 x2+18 x3 +19 x3+20 x4 +21 x4 +22 x2 ) / 29 ~16,6 cm.
4. Déterminer la médiane de cette série et interpréter le résultat.
La médiane est 18. 14 plantules ont une taille inférrieure à 18 cm et 14 plantules ont une taille supérieure à 18 cm.
5. On considère
qu’un élève a bien respecté le protocole si la taille de la plantule à
10 jours est supérieure ou égale à 14 cm. Quel pourcentage des élèves
de la classe a bien respecté le protocole ?
24 plantules sur 29 plantules ont une taille supérieure ou égale à 14 cm.
24 / 29 x100 ~82,8 %.
6. Le professeur a
fait lui-même la même expérience en suivant le même protocole. Il a
relevé la taille obtenue à 10 jours de germination. Prouver que, si on
ajoute la donnée du professeur à cette série, la médiane ne changera
pas.
Avec 30 valeurs, la médiane se situera entre la 15è et la 16é valeur, soit 18 cm.
|
|
|
Exercice 3.
Le poids d’un corps sur un astre dépend de la masse et de l’accélération de la pesanteur.
On peut montrer que la relation est P =mg ,
P est le poids (en Newton) d’un corps sur un astre (c’est-à-dire la
force que l’astre exerce sur le corps), m lamasse (en kg) de ce corps,
g l’accélération de la pesanteur de cet astre.
1. Sur la terre, l’accélération de la pesanteur de la Terre gT est environ de 9,8.
Calculer le poids (en Newton) sur Terre d’un homme ayant une masse de 70 kg.
P = mg = 70 x9,8 = 686 N.
2. Sur la lune, la relation P =mg est toujours valable. On donne le tableau ci-dessous de correspondance poids-masse sur la Lune :
Masse (kg)
|
3
|
10
|
25
|
40
|
55
|
Poids(N)
|
5,1
|
17
|
42,5
|
68
|
93,5
|
gL =Poids / masse
|
1,7
|
1,7
|
1,7
|
1,7
|
1,7
|
a. Est-ce que le tableau ci-dessus est un tableau de proportionnalité ?
Oui, le rapport Poids / masse est constant.
b. Calculer l’accélération de la pesanteur sur la lune noté gL
c. Est-il vrai que l’on pèse environ 6 fois moins lourd sur la lune que sur la Terre ?
La masse reste constante, mais le poids est divisé par 9,8 / 1,7 ~6.
3. Le dessin ci-dessous représente un cratère de la lune. BCD est un triangle rectangle en D.
a. Calculer la profondeur BD du cratère. Arrondir au dixième de km près.
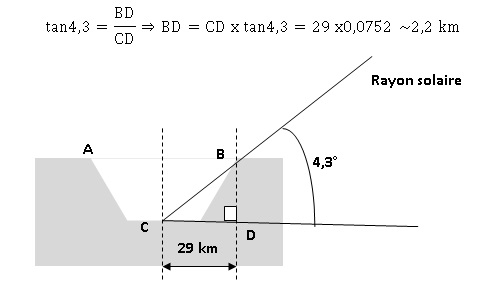
b. On considère que la longueur CD représente 20% du diamètre du cratère.
Calculer la longueur AB du diamètre du cratère.
29 / 0,20 =145 km.
Exercice 4.
On donne la feuille de calcul ci-contre.
La colonne B donne les valeurs de l’expression 2x2−3x−9 pour quelques valeurs de x de la colonne A.
1. Si on tape le nombre 6 dans la cellule A 17, quelle valeur va-t-on obtenir dans la cellule B 17 ?
2 x62-3x6-9=45
2. À l’aide du tableur, trouver 2 solutions de l’équation : 2x2−3x −9 = 0.
-1,5 et 3.
3. L’unité de longueur est le cm.
Donner une valeur de x pour laquelle l’aire du rectangle ci-dessous est égale à 5 cm2. Justifier.
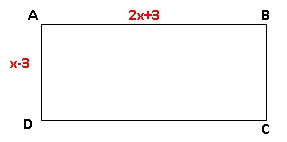
(2x+3)(x-3)=5
2x2-6x+3x-9=5
2x2−3x−9= 5.
x=3,5 cm
|
| A
|
B
|
|
x
|
2x2−3x−9 |
1
|
-2,5
|
11
|
2
|
-2
|
5
|
3
|
-1,5
|
0
|
4
|
-1
|
-4
|
5
|
-0,5
|
-7
|
6
|
0
|
-9
|
7
|
0,5
|
-10
|
8
|
1
|
-10
|
9
|
1,5
|
-9
|
10
|
2
|
-7
|
11
|
2,5
|
-4
|
12
|
3
|
0
|
13
|
3,5
|
5
|
14
|
4
|
11
|
15
|
4,5
|
18
|
16
|
5
|
26
|
17
|
6
|
|
|
.
|
|
|
|
Exercice 5.
Une pyramide régulière de sommet S a pour base le carré ABCD telle que son volume V est égal à 108 cm3.
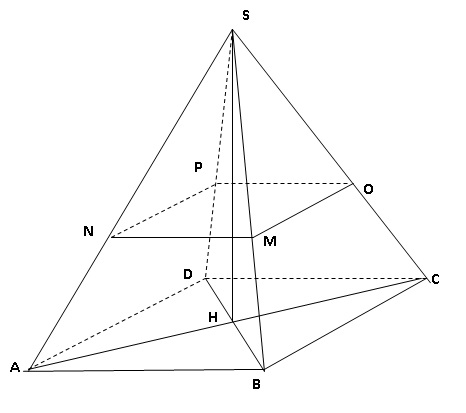
Sa hauteur [SH] mesure 9 cm.
Le volume d’une pyramide est donné par la relation :
Volume d’une pyramide = aire de la base×hauteur / 3.
1. Vérifier que l’aire de ABCD est bien 36 cm2. En déduire la valeur de AB.
Aire de base = 3 V / SH = 3 x108 /9 =36 cm2.
AB = racine carrée (36) = 6 cm.
Montrer que le périmètre du triangle ABC est égal à 12+6 x racine carrée(2) cm.
AB+BC+AC = 2 côtés du carré + diagonale du carré = 2 x6 + 6 x racine carrée (2) cm.
2. SMNOP est une réduction de la pyramide SABCD.
On obtient alors la pyramide SMNOP telle que l’aire du carré MNOP soit égale à 4 cm2.
a. Calculer le volume de la pyramide SMNOP.
Facteur de réduction OM / BC = 2 / 6 = 1 /3.
Hauteur de la petite pyramide : 1 / 3 x9 = 3 cm.
Volume de la petite pyramide : 4 x 3 / 3 = 4 cm3.
b.
Elise pense que pour obtenir le périmètre du triangle MNO, il suffit de
diviser le périmètre du triangle ABC par 3. Êtes-vous d’accord avec
elle ?
A convient.
Oui, le facteur de réduction est de1 / 3. Le préimètre du triangle MNO est égal au périmètre du triangle ABC divisé par trois.
|
|
Exercice 6.
Lancé le 26 novembre 2011, le Rover Curiosity de la NASA est chargé d’analyser la planète Mars, appelée aussi planète rouge.
Il a atterri sur la planète rouge le 6 août 2012, parcourant ainsi une distance d’environ 560 millions de km en 255 jours.
1. Quelle a été la durée en heures du vol ?
255 x24 =6120 heures.
2. Calculer la vitesse moyenne du Rover en km/h. Arrondir à la centaine près.
distance ( km ) / durée ( heure) = 560 106 / 6120 ~9,15 104 km /h.
3. Via le satellite Mars Odyssey, des images prises et envoyées par le Rover ont été retransmises au centre de la NASA.
Les premières images ont été émises de Mars à 7 h 48 min le 6 août 2012.
La distance parcourue par le signal a été de 248×106 km à une vitesse moyenne de 300 000 km/s environ (vitesse de la lumière).
À quelle heure ces premières images sont-elles parvenues au centre de la NASA ? (Arrondir à la minute près ).
distance ( km ) / vitesse ( km /s) = 248 106 / 300000=826,7 s ou 13 min 47 s ( 14 min).
heure d'arrivée : 7 h 48 + 14 min = 8 h 02 min.
|
|