Mathématiques,
Brevet des collèges Nlle Calédonie 03 /2013
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1. QCM
1.Trois mille trente et
trois centièmes s’écrit : 3030,03.
2. 2080+10+10
est égal à : 2100.
3. 3x * 2x est égal
à : 6x2.
4. Les solutions de
l’équation x(x + 7) = 0 sont : x=0 et x = -7.
5. 5×10−3
est égal à : 0,005.
6. Racine
carrée (16) + racine carrée (9)=racine carrée (42) +racine
carrée (32)= 4 +3 = 7.
7. Pierre va à vélo
au collège, il part à 6 h 38. Son trajet dure 25 minutes.
Les cours commencent à 7 h 05. Il arrivera : 6 h38 +25 min = 6 h 63 min
= 7 h 03 min.
8. Dans un jeu de
52 cartes, on tire une carte. Quelle est la probabilité que la carte
tirée soit un as ?
4 cas favorables sur 32 possibles. La probabilité de tirer un as
est 4 / 52 = 1 / 13.
Exercice
2.
Un oeuf de poule pèse en moyenne 63 grammes. Sachant que :
• le blanc d’oeuf est deux fois plus lourd que le jaune d’oeuf,
• le jaune d’oeuf est deux fois plus lourd que la coquille,
combien pèse la coquille d’un oeuf de poule ?
On note x le poids de la coquille.
Poids du jaune : 2x ; poids du blanc : 4x ; x+2x+4x = 7x = 63 ; x = 9.
Exercice 3.
La figure ci-dessous représente un trapèze rectangle
ABCD tel que :
AB = 12 cm ; CD = 9 cm ; BC = 5cm.
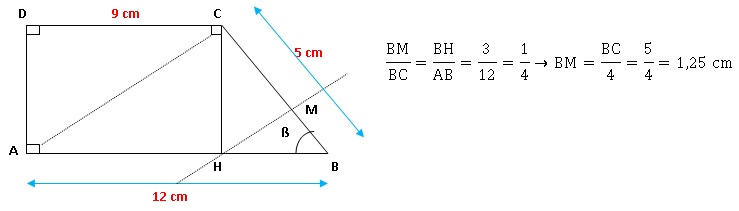
1. H est le pied de
la hauteur issue de C.
a. Montrer que HB =
3 cm.
AHCD est un rectangle ; AH = CD = 9 cm ; BH = AB -AH = 12 -9 = 3 cm.
b. Calculer CH.
CH2 = BC2-BH2 = 52-32
= 25-9 = 16 ; CH = 4 cm.
c. Déduire que le
périmètre de ABCD est égal à 30 cm.
AD + DC +CB +BA = 9 +5 +12 +4 = 30 cm
2. Calculer la
mesure de l’angle ß au degré près.
sin ß = CH / BC = 4 / 5 = 0,8 ; ß ~53°.
3. Représenter sur
la copie la figure aux dimensions réelles.
4. La parallèle à
(AC) passant par H coupe la droite (BC) en M. Compléter la figure.
5. Calculer BM.
|
|
|
|
Exercice 4.
Un
après-midi, Juliette observe son poisson Roméo en se plaçant au dessus
de son aquarium de forme sphérique. Elle remarque le drôle de manège de
son poisson nageant à la surface :
• il part d’une paroi de l’aquarium et nage 12 cm avant d’atteindre à
nouveau la paroi,
• il change alors de direction et nage encore 5 cm avant d’atteindre à
nouveau la paroi se trouvant alors en un point diamétralement opposé à
son point de départ,
• il rejoint directement son point de départ.
Le poisson effectue chaque déplacement en ligne droite.
1. Compléter la
figure en représentant le déplacement de Roméo à la surface de l’eau,
vu de dessus.
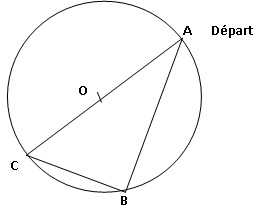
2. Quelle est la
nature de la figure parcourue par Roméo ? Justifier.
Le triangle ABC est inscrit dans un demi-cerccle de diamètre AC : il
est rectangle en B.
3. Calculer la
distance totale parcourue par Roméo.
CA2
= BC2+BA2 = 52+122 = 25+144
= 169 ; CA = 13 cm
13 +5 +12 = 30 cm.
Exercice
5.
Au lycée professionnel,
Jacques et Patrick, futurs maçons, s’entrainent en construisant un mur
chacun.
Leur professeur M. Ecker vient vérifier si chaque mur est bien « droit
», c’est-à-dire perpendiculaire au sol.
Ayant oublié sa caisse à outils dans son atelier, il ne possède que le
mètre ruban qu’il avait dans sa poche.
Pour chacun des murs, M. Ecker place au pied du mur un point I puis un
point H à 60 cm de hauteur sur le
mur et un autre point S au sol à 80 cm de I, puis il mesure la longueur
HS.
Pour le mur de Jacques il trouve 1 m et pour celui de Patrick 95 cm.
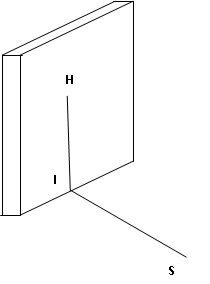
1. Le mur de
Jacques est-t-il « droit » ? Détailler votre raisonnement.
HS2 =12 = 1 ;
HI2+IS2 = 0,62+0,82 =
0,36+0,64 = 1 ;
HS2
=
HI2+IS2 , d'après la réciproque du théorème de
Pythagore, le mur est droit.
2. Et celui de Patrick ? Justifier.
HS2 =0,952 = 0,9025
; HI2+IS2 = 0,62+0,82
= 0,36+0,64 = 1 ;
HS2
diffère de HI2+IS2 , le mur
n'est pas droit.
|
|
|
|
Première partie.
A Poindimié, Torres possède un enclos de 18 animaux avec uniquement des
poules et des chèvres. Torres dit à son petit-fils : « Je compte 40
pattes, peux-tu me dire quel est le nombre de poules et le nombre de
chèvres dans mon enclos ? »Son petit-fils lui répond : « Eh bien ...
oui. »
Déterminer le
nombre de poules et le nombre de chèvres possédées par Torres.
On note x le nombre de poules et 18-x le nombre de chèvres.
2x +4(18-x) =40 ; 2x-4x+72 = 40 ; 2x = 32 ; x = 16 poules et 2 chèvres.
Deuxième partie.
Comme cuve de récupération d’eau de pluie, Torres utilise un pavé droit
dont les dimensions sont indiquées sur le schéma ci-dessous :
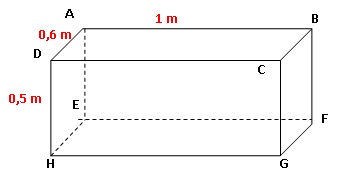
1. Montrer que le
volume de la cuve est de 300 000 cm3. En déduire sa
contenance en litres.
50 x60 x100 = 300 000 cm3= 300
L.
2. Montrer que
l’aire de la surface ABCD de récupération de l’eau de pluie est de 0,6 m2.
0,6 x1 = 0,6 m2.
3. La quantité
d’eau de pluie tombée au cours de l’année 2011 dans la commune où
habite Torres est de 2550 mm.
4. On précise que
1 mm d’eau récupéré, c’est 1 litre d’eau lorsque la surface est 1 m2.
a. Calculer
le volume maximal x d’eau récupérée en 2011 par Torres.
2550 x 0,6 = 1530 L.
5. En 2011, Torres
a récupéré 1 530 L d’eau de pluie.
li faut en moyenne 1,5 L d’eau par semaine pour abreuver une poule.
a. Torres a-t-il eu
suffisamment d’eau pour abreuver « gratuitement »ses 16 poules durant
l’année 2011 ? Justifier.
Rappel : il y a 52 semaines dans une année.
Les poules consomment en une semaine : 1,5 x16 = 24 L
et en une année : 24 x52 =1248 L, valeur inférieure à 1530. Il a
suffisamment d'eau.
b. Combien de
litres ne seront pas consommés ?
1530-1248=282 L.
c. En se basant sur
les résultats précédents, combien de poules supplémentaires pourrait-il
abreuver ?
282 / 52 ~5,4 L ; 5,4 / 1,5 ~ 3,6 soit 3
poules supplémentaires.
|
|