Mathématiques,
Brevet des collèges Polynésie 2012
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
1. L’
inverse de 1 est : 1.
2.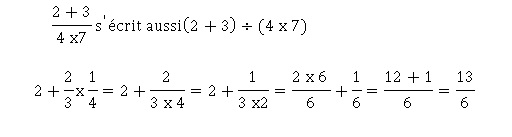
3. Si x = −4 alors x+4+(x+4)(2x−5) est égal à :
-4 +4 +(-4+4)(2*(-4)-5) = 0 +0 x(-13) = 0.
Exercice 2.
L’entreprise « Punu Pua Toro » vend des boîtes de corned-beef.
Ces dernières sont de forme cylindrique de 12 cm de diamètre et de 5 cm
de hauteur.
Elles sont rangées dans un carton de 84 cm de long, 60 cm de large et 5
cm de hauteur de façon à ce qu’elles se calent les unes contre les
autres.
1. Combien de
boîtes peut-on ranger au maximum dans un carton ?
84 / 12 = 7 sur la longueur.
60 / 12 = 5 sur la largeur.
7 x5 = 35 par rangée.
2. Calcule le PGCD
de 84 et 60.
Algorithme d'Euclide : 84 = 60 +24 : 60 = 2 x24 +12 ; 24 = 2 x12.
Le PGCD de 84 et 60 est égal à 12.
3. L’entreprise
peut-elle ranger dans ce carton des boîtes cylindriques de plus grand
diamètre de façon à ce qu’elles se calent les unes contre les autres ?
Justifie ta réponse.
Non, le PGCD de 84 et 60 est égal à 12.
Exercice 3.
L’hôtel « la ora na »accueille 125 touristes :
— 55 néo-calédoniens dont 12 parlent également anglais.
— 45 américains parlant uniquement l’anglais.
— Le reste étant des polynésiens dont 8 parlent également anglais.
Les néo-calédoniens et les polynésiens parlent tous le français.
1. Si je choisis un
touriste pris au hasard dans l’hôtel, quelle est la probabilité des
évènements suivants :
a. Évènement A : «
Le touriste est un américain »
45 cas favorables sur 125 possibles ; la probabilité est : 45 /
125 = 9 / 25 =0,36.
b. Évènement B : «
Le touriste est un polynésien ne parlant pas anglais »
125-55-45=25 polynésiens.
17 cas favorables sur 25 cas possibles : la probabilité est : 17 / 25 =0,68.
c. Évènement C : «
Le touriste parle anglais »
12 +45 +8 =65 touristes parlent anglais.
La probabilité de parler anglais est : 65 / 125 = 13 /25 =0,52.
2. Si j’aborde un
touriste dans cet hôtel, ai-je plus de chance de me faire comprendre en
parlant en anglais ou en français ? Justifie ta réponse.
55 +25 = 80 touristes parlent le français.
La probabilité de parler français est : 80 / 125 = 16 / 25 =0,64.
On a plus de chance de se faire comprendre en français.
|
|
|
Exercice 4.
Teva vient de construire lui-même sa pirogue.
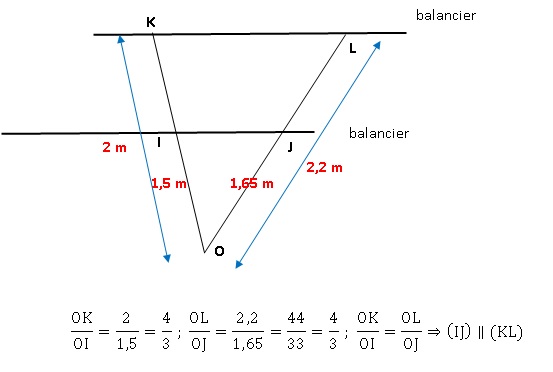
1. Pour
vérifier que les deux bras du balancier sont parallèles entre eux, il
place sur ceux-ci deux bois rectilignes schématisés sur le dessin
ci-dessus par les segments [OK] et [OL] avec I ∈ [OK] et J ∈ [OL].
La mesure des longueurs OI, OJ, OK et OL donne les résultats suivants :
OI = 1,5 m OJ = 1,65 m OK = 2m OL = 2,2 m.
Les deux bras sont-ils parallèles ? Justifie ta réponse.
2. Pour vérifier
que la pièce [AB] est perpendiculaire au balancier il mesure les
longueurs AB, AC et CB et obtient : AB= 15 cm ; AC = 25 cm ; CB= 20 cm
Peut-il affirmer que la pièce [AB] est perpendiculaire au balancier ?
Justifie ta réponse.
AC2 = 252 = 625.
AB2 +BC2 = 152 +202 = 225
+400 = 625.
AB2 +BC2 =AC2
;
d'après la réciproque du théorème de Pythagore, le triangle ABC est
rectangle en B.
|
|
|
|
Exercice 5.
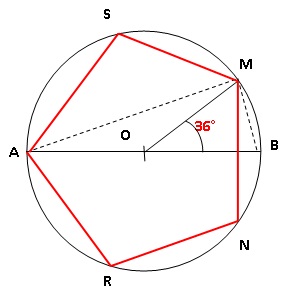
1. Trace le cercle
C de centre O et de diamètre [AB] tel que AB = 8 cm.
2. Place un point
M appartenant à C tel que ƒBOM= 36 °.
3. Calcule la
mesure de l’angle inscrit �MAB qui intercepte le petit arc de cercle MB.
La mesure de l'angle inscrit est égale à la moitié de la mesure de
l'angle au centre interceptant le même arc ;
l'angle MAB mesure 18°.
4. À l’aide des
données de l’énoncé, laquelle de ces propositions te permet de montrer
que AMB est un triangle rectangle en M :
Proposition 1
:
Si dans le triangle AME on a AB2= AM2 + BM2
alors AME est un triangle rectangle en M.
Proposition 2
:
Si le triangle AMB est inscrit dans le cercle C dont l’un des diamètres
est [AB] alors AMB est un triangle rectangle en M. Vrai.
Proposition 3
: Si O est le milieu de [AB] alors AMB est un triangle rectangle
d’hypothénuse [AB].
5. Calcule la
longueur AM et arrondis le résultat au dixième.
cos 18 = AM / AB ; AM = AB cos 18 = 8 x0,951 ~7,6 cm.
6. Trace le
symétrique N deM par rapport à [AB].
7. Place les points
R et S de façon à ce que NMRAS soit un pentagone régulier.
Le pentagone étant régulier, l'angle MON mesure 360 / 5 = 72°. Il
suffit de reporter l'arc MN à partir du point M.
Exercice 6.
Taraina
dirige une école de danse pour adolescents. Elle a relevé dans un
tableau l’âge de ses élèves ainsi que la fréquence des âges.
1. Complète sur
cette feuille le tableau suivant :
Age
des élèves
|
12
|
13
|
14
|
15
|
16
|
Total
|
Nombre
d'élèves
|
5
|
2
|
4
|
5
|
4
|
20
|
Fréquence
en %
|
5
/ 20 = 0,25
25 %
|
2
/ 20 = 0,10
10 %
|
20
|
25
|
20
|
100
|
2. Complète le
diagramme en barres des effectifs à l’aide du tableau précédent.
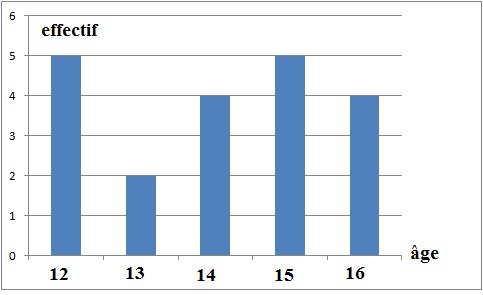
3. Quelle est dans
cette école la fréquence d’élèves ayant 14 ans ? 20 %.
4. Quel est le
nombre d’élèves âgés de 14 ans ou moins ? 5+2+4 = 11.
5. Taraina a
calculé que l’âge moyen de ses élèves est légèrement supérieur à 14
ans, or pour inscrire son groupe au Heiva dans la catégorie «
Adolescents », l’âge moyen du groupe doit être inférieur ou égal à 14
ans. Pour régler ce problème, elle a la possibilité d’accepter dans sa
troupe de danse un nouvel élève, soit de 13 ans, soit de 15 ans.
a. Lequel va-t-elle
choisir ? Pourquoi ?
Avec un nouvel élève de 13 ans, la moyenne vaut : (12 x 5 +13 x 3 +14
x4 +15 x5 +16 x4 ) / 21 = 14 ans.
Avec un nouvel élève de 15 ans, la moyenne vaut : (12 x 5 +13 x 3 +14
x4 +15 x6 +16 x4 ) / 21 = 14,7 ans.
b. Montre que l’âge
moyen de sa nouvelle troupe est maintenant de 14 ans.
|
|
Exercice 7.
Taraina veut inscrire ses 21 élèves aux festivités du Heiva. Deux
tarifs lui sont proposés :
Tarif Individuel : 500 F par danseur inscrit.
Tarif Groupe : Paiement d’un forfait de 4 000 F pour le groupe puis 300
F par danseur inscrit.
1. Complète le
tableau suivant :
Nombre
d'inscrits
|
0
|
10
|
25
|
Prix
au tarif individuel ( en F)
|
0
|
5000
|
25
x500 =12500
|
Prix
au tarif groupe ( en F)
|
0
|
7000
|
4000
+25 x300 = 11500
|
2.
Soit x le nombre d’inscriptions.
Le prix I (x) à payer si l’on choisit le tarif individuel en fonction
de x est I (x) = 500x.
Exprimer en fonction de x, le prix G(x) à payer si l’on choisit le
tarif Groupe.
G(x) = 4000 + 300x.
3. Dans le repère
ci-dessous construire la représentation graphique des deux fonctions
I(x)=500x et G(x)=300x +4000.
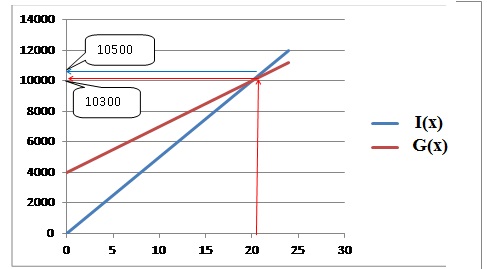
4. Graphiquement, quel est le tarif
le plus avantageux pour l’inscription des 21 élèves ?
Laisser apparaître les tracés utiles sur le graphique.
Le tarif groupe est le plus avantageux.
5. Pour quel nombre
d’inscriptions paye-t-on lemême prix quel que soit le tarif choisi ?
Justifie ta réponse par le calcul.
500 x = 4000 +300x ; 500 x -300x= 4000 ; 200x = 4000 ; x = 4000 / 200 ;
x = 20.
|
|