Mathématiques,
Brevet des collèges Amérique du Nord 2012
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
.
.
|
|
|
|
|
|
Exercice 1.
Quatre affirmations sont données ci-dessous.
Affirmation 1
: 1 /8 est un nombre décimal. Vrai
( 1/8 =0,125)
Affirmation 2
: 72 a exactement cinq diviseurs. Faux.
1 ; 2 ; 3 ; 4 ; 9 ; 8 ; 12 ; 24 ; 36 ; 72.
Affirmation 3
: Si n est un entier, (n −1)(n +1)+1 est toujours égal au carré d’un
entier. Vrai.
(n −1)(n +1)+1 =n2-1 +1 = n2.
Affirmation 4 : Deux
nombres impairs sont toujours premiers entre eux. Faux.
9 et 27 sont impairs ; ils admettent 9 comme diviseur commun. 9 et 27
ne sont pas premiers entre eux.
Pour chacune, indiquer si elle est vraie ou fausse en argumentant la
réponse.
Exercice 2.
Deux classes du collège ont répondu à la question suivante :
« Combien de livres avez-vous empruntés durant les 12 derniers mois ? »
Les deux classes ont communiqué les réponses de deux façons différentes
:
Classe n° 1 : 1 ; 2 ; 2 ; 2 ; 2 ; 3 ; 3 ; 3 ; 3 ; 3 ; 3 ; 3 ; 3 ; 6 ; 6
; 6 ; 6 ; 6 ; 7 ; 7 ; 7
Classe n° 2 : Effectif total : 25
Moyenne : 4 ; Étendue : 8 ; Médiane : 5.
1. Comparer les
nombres moyens de livres empruntés dans chaque classe.
Classe n°1 : moyenne = (1 +2 x 4 +3 x8 + 5 x 6 + 3 x7) / 21 =4.
Les moyennes sont identiques.
2. Un « grand
lecteur » est un élève qui a emprunté 5 livres ou plus. Quelle classe a
le plus de « grands lecteurs » ?
Classe n°1 : 8 grands lecteurs. La médiane est égale à 3
Classe n° 2 : la médiane est égale à 5 ; 25 / 2 = 12,5 , 12 élèves sont
grands lecteurs.
3. Dans quelle
classe se trouve l’élève ayant emprunté le plus de livres ?
Classe n°1 : étendue 7-1 = 6.
Classe n°2 : l'étendue est égale à 8 ; dans cette classe un élève a
emprunté au moins 8 livres.
|
|
|
Exercice 3.
Léa observe à midi, au microscope, une cellule de
bambou.
Au bout d’une heure, la cellule s’est divisée en deux. On a alors deux
cellules.
Au bout de deux heures, ces deux cellules se sont divisées en deux.
Léa note toutes les heures les résultats de son observation.
À quelle heure notera-t-elle, pour la première fois, plus de 200
cellules ?
Temps
(heure )
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Nombre
de cellules
|
2
|
4
= 22
|
8
= 23.
|
16
= 24.
|
25
=32
|
26
=64 |
27
=128 |
28
=256 |
Exercice 4.
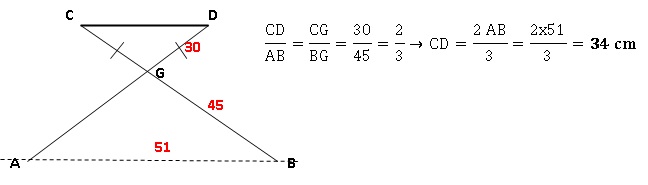
On
a modélisé géométriquement un tabouret pliant par les segments [CB] et
[AD] pour l’armature métallique et le segment [CD] pour l’assise en
toile.
On a CG = DG = 30 cm, AG = BG = 45 cm et AB = 51 cm.
Pour des raisons de confort, l’assise [CD] est parallèle au sol
représenté par la droite (AB).
Déterminer la longueur CD de l’assise.
|
|
|
|
Exercice 5.
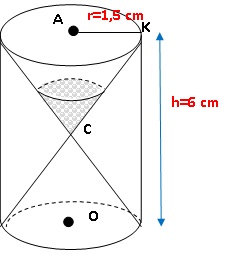
On
considère un sablier composé de deux cônes identiques de même sommet C
et dont le rayon de la base est AK = 1,5 cm. Pour le protéger, il est
enfermé dans un cylindre de hauteur 6 cm et de même base que les deux
cônes.
1. On note V le
volume du cylindre et V1 le volume du sablier. Tous les
volumes seront exprimés en cm3.
a. Montrer que la
valeur exacte du volume V du cylindre est 13,5 p.
V = pr2
h = p x1,52
x 6 = 13,5 p cm3.
b. Montrer que la
valeur exacte de V1 est 4,5 p.
Volume des deux cônes : V1 = 2 /3 x ( pr2 h / 2) =2 / 3
( p x1,52
x 3 )=2 xp x1,52
=4,5 p cm3.
c. Quelle fraction
du volume du cylindre, le volume du sablier occupe-t-il ?
(On donnera le résultat sous la forme d’une fraction irréductible).
4,5 / 13,5 = 1 / 3.
2. On amis 12 cm3
de sable dans le sablier.
Sachant que le sable va s’écouler d’un cône à l’autre avec un débit de
240 cm3 /h, quel temps sera mesuré par ce sablier ?
12 / 240 = 0,05
heure ou 0,05 x60 = 3 minutes.
Exercice 6.
Construire un carré dont l’aire est égale à la somme des aires des deux
carrés représentés ci-dessous.
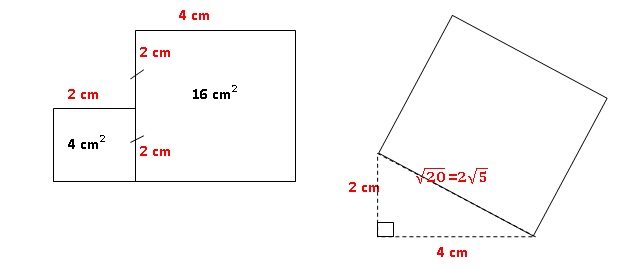
Construire un triangle rectangle dont les côtés de l'angle droit
mesurent 2 et 4 cm.
Construire un carré dont l'un des côtés est l'hypothénuse de ce
triangle.
|
|
Exercice 7.
Dans
un collège de Caen (Normandie) est organisé un échange avec le Mexique
pour les élèves de 3e qui étudient l’espagnol en seconde langue.
Partie 1 -
L’inscription des élèves
Le tableau ci-dessous permet de déterminer la répartition de la seconde
langue étudiée par les 320 élèves de 4e et de 3e de ce collège.
Secone
langue étudiée
|
4e
|
3e
|
Total
|
|
|
|
|
Espagnol
|
84
|
162-84
=78
|
320
-112 -46 =162
|
Allemand
|
22
|
24
|
22+24=46
|
Italien
|
62
|
50
|
50+62
= 112
|
Total
|
|
|
320
|
1. Combien
d’élèves peuvent être concernés par cet échange ? 78.
2. 24 élèves vont
participer à ce voyage. Est-il vrai que cela représente plus de 12% des
élèves de 3e ?
12 *162 / 100 = 19,44 ( 19 élèves). 24 / 162 x100 = 14,8 %.
24 élèves représentent 14,8 % des élèves de 3e.
Partie II - Le
financement
Afin de financer cet échange, deux actions sont mises en oeuvre : un
repas mexicain et une tombola.
1. Le repas
mexicain, où chaque participant paye 15 €.
Au menu, on trouve un plat typique du Mexique, le Chili con carne.
Recette pour 4 personnes
50 g de beurre 500 g de boeuf haché
2 gros oignons 65 g de concentré de tomate
2 gousses d’ail
30 cl de bouillon de boeuf 400 g de haricots rouges
50 personnes participent à ce repas.
a. Donner la
quantité de boeuf haché, de haricots rouges, d’oignons et de concentré
de tomate nécessaire.
500 x50 / 4 = 6 250 g = 6,25 kg
de boeuf.
400 x50 / 4 = 5000 g =
5 kg de haricots.
2 x50 / 4 = 25 oignons.
65 x50 / 4 = 812,5 g de
concentré de tomate.
b. Les dépenses
pour ce repas sont de 261 €, quel est le bénéfice ?
50 x15 -261 =489 €.
2. La tombola, où
720 tickets sont vendus au prix de 2 €.
Les lots sont fournis gratuitement par trois magasins qui ont accepté
de sponsoriser le projet.
Il y a trois lots à gagner : un lecteur DVD portable, une machine à
pain et une mini-chaîne Hifi.
Un élève achète 1 ticket.
a. Quelle
probabilité a-t-il de gagner l’un des lots ?
3 cas favorables sur 720 possibles ; la probabilité de gagner est 3 /
720 = 1 / 240~0,0042.
b. Quelle
probabilité a-t-il de gagner la mini-chaîne Hifi ?
1 / 720.
3. Montrer que la
somme récupérée par les deux actions est de 1 929 €.
720 x 2 + 489 = 1929 €.
Partie II - Le
voyage
Le voyage se décompose en deux parties : le trajet Caen-Paris (256 km)
se fait en bus puis le trajet Paris-Mexico (9 079 km) en avion.
1. Le prix d’un
billet d’avion aller-retour coûte 770,30 € par personne.
L’argent récolté par le repas mexicain et la tombola permet de réduire
équitablement ce prix pour les 24 élèves participants.
Quelle est la participation demandée par élève pour les billets d’avion
? (arrondir à l’unité).
1929 / 24 = 80,375 €.
770,30 -80,375 = 689,925 ~690 €.
2. Le décollage se
fait à 13 h 30. Cependant, les élèves et les accompagnateurs doivent
être impérativement à l’aéroport de Paris-Roissy à 11 h 30.
On estime la vitesse moyenne du bus à 80 km/h. Jusqu’à quelle heure
peut-il partir de Caen ?
Durée du voyage en bus : 256 / 80 = 3,2 heures ou 3 h 12 min.
11 h30. -3 h 12 = 8 h 18 min.
3. L’avion arrive à
Mexico à 17 h 24 heure locale. Il faut compter 7 heures de décalage
avec la France.
a. Quelle est la
durée du trajet ?
7 h + 17 h24 - 13 h30 = 7 h + 3 h 54 min = 10 h 54 min.
b. Quelle est la
vitesse moyenne de l’avion? (arrondir à l’unité)
54 / 60 = 0,9 h ; durée du voyage : 10,9 h ; vitesse moyenne : 9079 /
10,9 ~833 km /h.
|
|