Mathématiques,
bac biotechnologies Métropole 09/ 2017.
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
QCM. 4 points.
Pour chacune des questions, une seule des trois réponses proposées est
exacte.
Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs
réponses ou l’absence de
réponse à une question ne rapportent ni n’enlèvent de point.
Indiquer, sans justification, le numéro de la question et la réponse
correspondante .
1. Une variable
aléatoire X suit la loi uniforme sur [4 , 9], alors la probabilité P(X
≥ 5) est égale à :
a) 5 / 9 ; b) 0,8 exact ; c) une valeur autre que 5 /
9 et 0,8.
P(X > 5)
=P(5 < X < 9)= (9-5) / (9-4) = 4
/ 5 = 0,8.
2. Une variable
aléatoire Y suit la loi normale d’espérance 15 et d’écart type 4 alors
la probabilité
P(Y ≥ 17) est :
a) supérieure à 0,25 exact ;
b) inférieure à 0,15 ; c) supérieure à 0,75.
P(X > 17) = 1- P(X
<17) =
1-0,691 = 0,309.
3. Dans le repère
ci-dessous, la courbe Cf représente la fonction de densité f
d’une variable
aléatoire suivant une loi normale d’espérance μ et d’écart type σ. De
même, la courbe Cg
représente la fonction de densité g d’une variable aléatoire suivant
une loi normale d’espérance
μ' et d’écart type σ'.
D’après le graphique, on a :
a) μ = μ' et σ > σ' exact ;
b) μ < μ' et σ = σ' ; c) μ = μ' et σ < σ' .
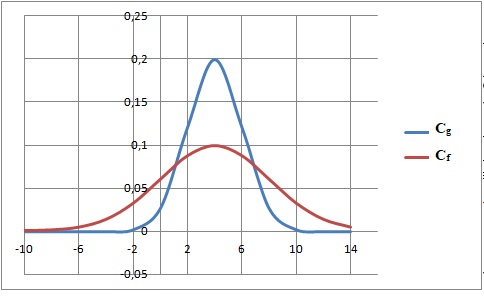
µ =µ'= 4.
L'écart type mesure la dispersion autour de la moyenne. La courbe
Cf est plus étalée que la courbe Cf, donc s' < s.
4. La loi binomiale
de paramètres n = 150 et p = 0,96 peut être approximée par la loi
normale
d’espérance μ et d’écart type σ avec :
a) μ = 144 et σ = 5,76 ; b) μ = 150 et σ = 2,4 ; c) μ = 144 et σ = 2,4, exact.
µ = np = 150 x0,96 =144.
s =
(np(1-p))½ = (150 x0,96 x0,04)½ = 2,4.
|
....
.....
|
Exercice
2. (4 points)
Une
solution contient initialement 5 millions de bactéries par mL. Toutes
les 10 minutes, la concentration en bactéries augmente de 15 %.
1. Pour tout entier
naturel n, on note cn la concentration en bactéries en
millions par mL au bout de n dizaines de minutes.
a) Quelle est la
nature de la suite (cn) ? En préciser le premier terme et la
raison.
On passe d'un terme au suivant en le multipliant par 1,15. Donc suite
géométtrique de premier terme c0=5 et de raison q = 1,15.
b) Vérifier qu’au
bout d’une heure et demie, la concentration des bactéries en millions
par mL, est égale à 17,6 (valeur arrondie à 0,1).
1,5 h = 90 minutes.
u9 = 5 x1,159 ~17,6.
c) En précisant la
démarche, déterminer au bout de combien de minutes la concentration en
bactéries dépasse 20 millions par mL.
5 x1,15n> 20 ; 1,15n>
4 n ln(1,15) > ln 4 ; n > ln 4 / ln(1,15) ; n >9,92.
Soit environ 100 minutes.
Les phages sont des virus infectant les bactéries ; ils peuvent donc
servir d'agents antibactériens. Le but de l'exercice est d'étudier
l'action de phages sur une population de bactéries.
2. On introduit des
phages au bout de 90 minutes. Cette introduction de
phages provoque une diminution globale de la concentration en bactéries
de 40 % toutes les dix minutes. On souhaite connaître le temps
nécessaire pour que la concentration en bactéries devienne inférieure à
10 % de la concentration initiale. Pour ce faire, on utilise
l'algorithme ci-dessous.
Variables : I entier, C réel
Traitement :
C prend la valeur 17,6
I prend la valeur 0
Tant que C > 0,5
I prend la valeur I+1
C prend la valeur Cx0,6
Fin Tant Que
Sortie : Afficher I et C
a) Que
représentent les valeurs 17,6 et 0,5 figurant dans l’algorithme par
rapport à la situation concrète proposée ?
A la date t = 90 minutes, on introduit les virus. Le nombre de
bactéries est alors égal à 17,6 millions.
Concentration initiale des bactéries : 5 millions par mL ; 10 %
de 5 millions = 0,5 millions. L'algorithme tourne tant que C > 0,5.
b) Quelles sont les
valeurs affichées par l’algorithme en sortie ? Comment les interpréter ?
I
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
C
|
17,6
|
17,6
x0,6 = 10,56
|
10,56
x0,6= 6,336
|
6,336
x0,6=3,80
|
3,80
x0,6=2,28
|
2,28
x0,6 ~1,37
|
1,37
x0,6 ~0,82
|
0,82
x0,6 ~ 0,49
|
Au bout de 70 minutes la
concentration des bactéries est inférieure à 0,5 millions par mL.
|
|
|
Exercice
3.
Partie A
Chez un ostréiculteur (producteur d’huîtres) d’un village au bord de
l’Atlantique, la bactérie appelée
vibrio estuarianus est apparue à partir du mois d’août 2014. Le tableau
ci-dessous donne la quantité yi (exprimée en tonnes)
d’huîtres affectées par cette bactérie dans son élevage en fonction de xi
qui représente le numéro du mois depuis l’apparition de la bactérie. Le
numéro 1 correspond au mois d’août 2014, le numéro 2 correspond au mois
de septembre 2014, …
xi
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
yi
|
20
|
210
|
320
|
390
|
440
|
480
|
510
|
540
|
560
|
570
|
1. a) Représenter
graphiquement ce nuage de points dans un repère orthogonal.
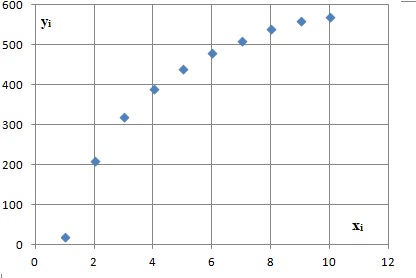
b) Un ajustement
affine semble-t-il pertinent ? Pourquoi ?
Les points n'étant pas alignés, un ajustement affine n'est pas
pertinent.
2. On pose : zi
= 750 /(750-yi).
. Recopier et compléter le tableau suivant en arrondissant les valeurs
de zi au centième.
xi
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
zi
|
1,03
|
1,39
|
1,74
|
2,08
|
2,42
|
2,78
|
3,13
|
3,57
|
3,95
|
4,17
|
3. a) On réalise alors un ajustement
affine de ce nouveau nuage de points Mi (xi , zi).
À l’aide de la
calculatrice, donner une équation de la droite D d’ajustement de z en x
obtenue par la méthode
des moindres carrés (on arrondira les coefficients à 10-4).
z =0,3566 x +0,6647.
b) Déterminer à
l’aide de ce modèle d’ajustement, la quantité d’huîtres affectées par
la bactérie
en décembre 2015 chez cet ostréiculteur (le mois de décembre est la
période de vente la plus
importante pour un ostréiculteur). On arrondira le résultat à la
dizaine de tonnes
x=17 ; z =0,3566 x17 +0,6647 =6,7269.
750 /(750-y)=6,7269 ; 750-y=111,49 ; y =638,5 ~640.
Partie B
Depuis le mois de janvier 2015, on tente d’éradiquer cette bactérie à
l’aide d’un antibiotique mis au
point par un laboratoire pharmaceutique. Le directeur de ce laboratoire
affirme que cet antibiotique
permet de sauver 76 % des huîtres affectées par cette bactérie.
1. Déterminer
l’intervalle de fluctuation asymptotique à 95 % de la fréquence
d’huîtres sauvées par
l’utilisation de l’antibiotique dans un échantillon de 1000 huîtres (on
arrondira les bornes de
l’intervalle à 10-3).
n =1000 > 30 ; np = 1000 x0,76 = 760 > 5 ; n(1-p) = 1000 x0,24 =
240 > 5.
Les conditions sont vérifiées pour déterminer un intervalle de
fluctuation asymptotique au seuil de 95 %.
1,96(0,76 x0,24 / 1000)½ =0,0261.
Intervalle de fluctuation : [0,76 -0,0261 ; 0,76 +0,0261] soit [0,734 ;
0,786]
2. L’ostréiculteur décide d’utiliser cet antibiotique sur un lot de
1000 huîtres de son élevage
affectées par cette bactérie. Il constate, qu’après l’utilisation de
cet antibiotique, 74 % des huîtres
ont été sauvées.
L’observation faite par l’ostréiculteur remet-elle en question
l’affirmation faite par le directeur du
laboratoire ? Justifier la réponse.
0,74 appartient à l'intervalle précédent. Au risque de 5 %, il n'y a
pas de raison de mettre en cause l'affirmation du directeur.
|
|
|
|
Exercice 4 ( 7
points)
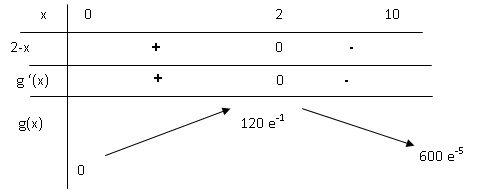
1. Soit la fonction
g définie sur [0, 10] par g(x) = 60 x e-0,5x .
À l’aide d’un logiciel de calcul formel, on obtient deux expressions de
la dérivée de la fonction g :
g'(x) = -30(x-2) e(-0,5x).
a) Déterminer le
signe de la dérivée de la fonction g.
e-0,5x est toujours positif. Le signe de la dérivée est le
signe de 30(x-2) soit le signe de 2-x.
g'(x) >0 sur [0 ; 2[ ; g(x) est strictement croissante.
g'(x) < 0 sur ]2 ; 10] ; g(x) est strictement décroissante.
g'(x) = 0 pour x = 2 ; g(x) présente un maximum.
b) Établir le
tableau de variations de g sur [0, 10]
.
2. Un laboratoire
teste l’efficacité d’une nouvelle crème solaire. Pour cela, il mesure
le taux d’hydratation, en pourcentage, de la peau d’une personne, qui
est exposée au soleil pendant 10 heures. On admet que pour tout réel t
de [0, 10], g(t) est le taux d'hydratation de la peau au
bout de t heures après l’application de la crème.
a) Calculer le taux
d’hydratation, en pourcentage, de la peau au bout d’une demi-heure
après l’application de la crème. On arrondira au dixième
g(0,5) = 60 x0,5 e-0,25 =23,4 %..
b) Déterminer à
quel moment le taux d’hydratation, en pourcentage, est maximal
L'étude de la fonction g indique un taux d'hydratation maximal au bout
de 2 heures..
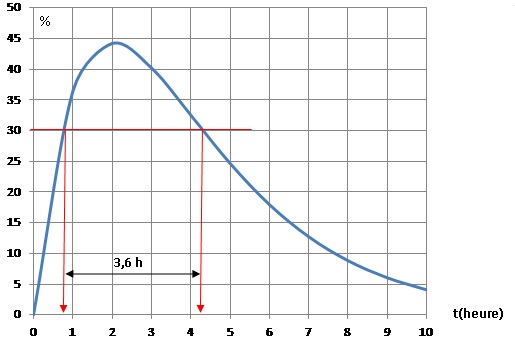
c) On peut
commercialiser cette crème si le taux d’hydratation dépasse 30 %
pendant une durée d’au moins 3 heures.
À l’aide de la représentation graphique Cg de la fonction g
donnée, expliquer si le laboratoire peut ou non commercialiser cette
crème (on fera notamment apparaître les traits de construction utiles).
Cette crème est commercialisable.
3. Un chercheur du
laboratoire étudie l’élimination au contact de la lumière d’un
composant de la crème solaire. La concentration de ce composant est
modélisée par une fonction f.
Lorsque t représente le temps d’exposition à la lumière, en heures, f
(t) représente la concentration en g L-1 de ce composant
restant dans la crème.
On admet que la fonction f définie sur [0 , +∞[ est solution de
l’équation différentielle suivante :
(E) : y'+ 0,4y = 0 .
a) On sait qu’à
l’instant t = 0, la concentration du composant est égale 1,3 g L-1.
Montrer alors que pour tout réel t de [0 , +∞[, f(t) = 1,3 e-0,4t.
Solution générale de (E) ; y = A e-0,4t, avec A une
constante déterminée par la condition initiale.
y(0) = A = 1,3.
b) Déterminer le
sens de variation de la fonction f sur l’intervalle [0 , +∞[.
Ce résultat est-il cohérent avec la situation étudiée ? Pourquoi ?
f '(t) = 1,3 (-0,4) e-0,4t = -0,52 e-0,4t.
Le terme en exponentielle étant toujours positif, f '(t) est négative
et f(t) est strictement décroissante.
Ce résultat est cohérent, le composant s'élimine au contact de la
lumière au cours du temps.
c) Déterminer, au
bout de combien de temps, la concentration du composant est inférieure
à 0,3 g L-1. On donnera la valeur en heures et minutes,
arrondie à la minute.
1,3 e-0,4t < 0,3 ; e-0,4t <0,3 / 1,3 ; -0,4
t < ln(0,3 / 1,3) ; t > ln(1,3 / 0,3) / 0,4 ; t >3,666 heures.
soit t > 3 h40 min.
|
|