Mathématiques, bac SPCL Métropole 09/ 2017.

Mathématiques, bac SPCL Métropole 09/ 2017.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

QCM. 4 points
1. On donne ci-dessous la courbe C représentative d’une fonction f définie et dérivable sur [0 ; +∞[.

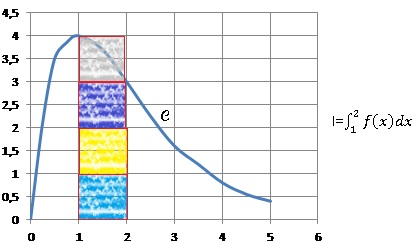
Un encadrement de I est :
a. 6 < I < 8 ; b. 1 < I < 2 ; c. 3 < I < 4 exact; d. 13 < I < 16.

2. La fonction g est définie sur l’intervalle ]0 ; +∞[ par g (x)= (−2x +1) ln(x)+5.
La limite de cette fonction g en +∞est égale à :
a. +∞ ; b. −∞ exact ; c. 0 ; d. 5.
Quand x tend vers plus l'infini : ln(x) est positif et tend vers plus l'infini ; -2x+1 est négatif et tend vers moins l'infini; (-2x+1) ln(x) est négatif et tend vers moins l'infini.

3. La suite (v_n) est géométrique de premier terme v₀ = 4 et de raison q = 0,5.
La somme des 9 premiers termes de cette suite est égale à :
a. 4×0,5⁸ ; b. (1−0,5⁹) / (1−0,5) ; c. 8×(1−0,5⁹) exact ; d. 6,9.
S =v₀(1-0,5⁸⁺¹) / (1-0,5) = 4(1-0,5⁹) / 0,5 = 8×(1−0,5⁹).

4. La suite (u_n) est la suite géométrique de premier terme u₀ = 300 et de raison q = 1,05. L’algorithme
qui calcule et affiche tous les termes strictement inférieurs à 450 de cette suite est :

Variables
n : un nombre entier naturel
u : un nombre réel
Initialisation
n prend la valeur 0
u prend la valeur 300
Traitement
Tant que n < 450 erreur
Afficher u
n prend la valeur n +1
u prend la valeur 300×1,05n

Fin Tant que
Variables
u : un nombre réel
Initialisation
u prend la valeur 300
Traitement
Tant que u < 450
u prend la valeur 1,05×u
Fin Tant que
Sortie
Afficher u erreur
u est afficher une seule fois

Variables
u : un nombre réel
Initialisation
u prend la valeur 300
Traitement
Tant que u < 450
Afficher u
u prend la valeur 1,05×u
Fin Tant que
Variables
n : un nombre entier naturel
u : un nombre réel
Initialisation
n prend la valeur 0
u prend la valeur 300
Traitement
Tant que u < 450
n prend la valeur n +1
u prend la valeur 1,05×u
Fin Tant que
Sortie
Afficher u erreur
u est afficher une seule fois

a.

b.

....

.....
Exercice 2. (6 points)
Le stimulateur cardiaque est un appareil destiné à certaines personnes dont le rythme du coeur est devenutrop lent. Implanté sous la peau, l’appareil envoie des impulsions électriques régulières au coeurlorsque le rythme cardiaque est insuffisant.
Un stimulateur cardiaque est constitué de deux composants :
• un condensateur de capacité C égale à 4×10⁻⁷ farad ;
• un conducteur ohmique de résistance R égale à 2×10⁶ ohms.
Une fois le condensateur chargé, la tension à ses bornes est égale à 5,6 volts. Il se décharge ensuite dans le conducteur ohmique.
Partie A.
La tension u, en volts, aux bornes du condensateur est une fonction du temps t , en secondes. On admet que u(0) = 5,6 et que cette fonction u, définie et dérivable sur l’intervalle [0 ; +∞[, vérifie pour tout nombre t de l’intervalle [0 ; +∞[ la relation :
u′(t )+1 / (RC )×u(t ) = 0, où u′ désigne la fonction dérivée de la fonction u.
1. a. Vérifier que la fonction u est solution sur l’intervalle [0 ; +∞[ de l’équation différentielle
y′ +1,25y = 0.
RC = 2 10⁶ x4 10^-7 = 0,8 ; 1 / 5RC) = 1 / 0,8 = 1,25.
b. Résoudre l’équation différentielle y′ +1,25y = 0.
y = A exp(-1,25 t) avec A une constante définie par la condition initiale u(0) = 5,6 V.
c. Montrer que pour tout nombre réel t de l’intervalle [0 ; +∞[, on a : u(t ) = 5,6 e^−1,25t .
u(0) = A e⁰ = 5,6 ; A = 5,6. u(t ) = 5,6 e^−1,25t .
2. a. Étudier mathématiquement le sens de variation de la fonction u sur l’intervalle [0 ; +∞[.
b. Ce résultat était-il prévisible. Justifier la réponse.
u'(t) = 5,6 x(-1,25) e^-1,25t = - 7e^-1,25t.
Le terme en exponentielle étant positif, u'(t) est négative et u(t) est strictement décroissante de 5,6 V à zéro.
Cela était prévisible, la tension aux bormes d'un condensateur déchargé est nulle.

Partie B.
En réalité, lorsque la tension u aux bornes du condensateur a perdu 63% de sa valeur initiale u(0), le stimulateur cardiaque envoie une impulsion électrique au coeur, ce qui provoque un battement. Onconsidère que le condensateur se recharge instantanément et que la tension mesurée à ses bornes est à nouveau égale à 5,6 volts.
1. a. Vérifier que la tension aux bornes du condensateur qui déclenche l’envoi d’une impulsion
électrique au coeur est de 2,072 volts.
5,6 x (1-0,63) = 2,072 V.
b. Résoudre dans l’intervalle [0 ; +∞[ l’équation :
5,6 e ^-1,25t= 2,072.
c. Interpréter le résultat trouvé.
e ^-1,25t= 2,072 / 5,6 = 0,37.
-1,25t = ln(0,37) ; t = -ln(0,37 / 1,25 ~0,8 s.
Toutes les 0,8 s le coeur est stimulé.
2. Chez l’adulte en bonne santé, le pouls au repos se situe entre 50 et 80 pulsations par minute.
On admet que le stimulateur cardiaque d’un patient souffrant d’insuffisance envoie une impulsion
électrique au coeur toutes les 0,8 secondes.
Ce rythme correspond-il à celui d’un adulte au repos et en bonne santé ? Justifier la réponse.
Nombre d'impulsions par minute :60 /0,8 =75.
Cette valeur étant comprise entre 50 et 80, ce rythme correspond à celui d'un adulte au repos et en bonne santé.

Nombres complexes (5 points)
Les partie A et B sont indépendantes.
Partie A.
Dans le plan complexe muni d’une repère orthonormé direct , on représente les extrémités des pales d’une éolienne par le point A de coordonnées (0 ; 3) et par les points B et C d’affixes respectives :

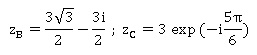
1. Soit z_A l’affixe du point A.
a. Donner la forme algébrique de z_A.
b. Donner la forme exponentielle de z_A.
Module de z_A = 3 ; z_A / |z_A| = 0 +i = sin( p/2) ; z_A = 3 exp(ip/2)= 3 i.
2. Déterminer la forme exponentielle de z_B.

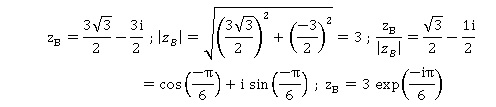
3. On admet que lorsque l’hélice tourne d’un angle de 90 degrés dans le sens direct, les points A, B et C sont transformés respectivement en A′, B′ et C′ tels que :
• A′ a pour affixe z_A′ = z_A × e^ip/2.
• B′ a pour affixe z_B′ = z_B × e^ip/2.
• C′ a pour affixe z_C′ = z_C× e^ip/2.
Déterminer la forme exponentielle de z_C′ .
zC' = 3 exp(i (-5p/6 +p/2)) =3 exp(-ip/3).

Partie B.
La durée de vie, en jours, d’un des composants électroniques d’une éolienne est modélisée par une variable aléatoire T qui suit la loi exponentielle de paramètre l= 0,002.
1. Calculer la durée de vie moyenne, en jours, d’un composant de ce type.
1 / 0,002 = 500 jours.
2. a. On considère la fonction f définie sur [0 ; +∞[ par f (x) = 0,002 e^−0,002x .
Montrer que la fonction F définie sur l’intervalle [0 ; +∞[ par F(x) = −e^−0,002x est une primitive de la fonction f sur l’intervalle [0 ; +∞[.
F '(x) = -(-0,002)e^−0,002x = 0,002 e^−0,002x = f(x).
b. On a donc P(T < t ) = 1− e^−0,002t .
Le fabricant affirme : « la probabilité que la durée de vie du composant soit supérieure à 100 jours est d’au moins 0,8. » Que penser de cette affirmation? Justifier la réponse.
P(T < t ) = 1− e^−0,002x100 ~0,1813.
P(T > 100) = 1-0,1813 ~0,82. L'affirmation est vraie.

Exercice 4 ( 5 points)
L’entreprise COFRUIT fabrique de la confiture de fruits, qu’elle conditionne en pots. Il est indiqué 680 grammes de confiture sur l’étiquette du pot.
En fin de chaîne de remplissage, les pots sont pesés et ceux dont la masse de confiture est strictement inférieure à 675 grammes ne sont pas commercialisés.
Partie A.
Après remplissage, la masse de confiture dans un pot est modélisée par une variable aléatoire X qui suit la loi normale d’espérance μ = 680 et d’écart-type s = 2,65.
1. Calculer la probabilité que la masse de confiture d’un pot, pris au hasard dans la production, soit comprise entre 677 grammes et 683 grammes.
P (X < 677) =0,1288 ; P (X < 683) =0,8712 ; P (677 < X < 683) =0,8712-0,1288 ~0,742.
2. Calculer la probabilité qu’un pot pris au hasard dans la production soit commercialisé.
P(X >675) = 1 -P(X < 675) =1-0,0296 ~ 0,970.
Partie B.
Dans cette partie, on considère qu’une machine de remplissage de pots est bien réglée lorsque la proportion théorique de pots non commercialisables est inférieure ou égale à 3%. On s’intéresse à la production journalière de pots remplis par cette machine.
1. Lors d’un contrôle de qualité, il est relevé que, sur un échantillon de 200 pots, 8 ne sont pas commercialisables.
À l’aide d’un intervalle de fluctuation asymptotique à 95%, déterminer si la machine nécessite un réglage.
n = 200 >30 ; np = 200 x0,03 = 6 > 5 ; n(1-p) = 200 x0,97 = 194 > 5.
Les critères sont réunis pour déterminer un intervalle de fluctuation au seuil de 95 %.
1,96 ((p(1-p)/n)^½ =0,236.
Intervalle de fluctuation [0,3-0,236 ; 0,3 +0,236 ] soit [0,064 ; 0,54 ].
La valeur 8 / 200 = 0,4 appartient à cet intervalle.
Au risque de 5%, la machine ne nécessite pas de réglage.
2. On rappelle dans cette question que μ = 680 et s = 2,65.
On suppose que la machine est bien réglée. L’entreprise décide de vendre les pots de confiture par lots de 2. Les lots de moins de 1350 grammes de confiture sont jugés non conformes.
On admet que la masse de confiture, en grammes, d’un lot de 2 pots est une variable aléatoire Y qui suit la loi normale d’espérance 2μ et d’écart-type 2^½s~3,75.
a. Calculer P(Y <1350).
P(Y <1350) ~ 0,00383.
b. Pourquoi est-il alors plus intéressant pour l’entreprise COFRUIT de vendre ses pots de confiture par lots de 2 ?
Le nombre lot de 2 pots de confiture non comforme n'est que de 0,38 % alors qu'il est de 3% lors d'une vente à l'unité.

.

menu