Mathématiques,
bac
STL biotechnologies Métropole 2017.
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice 1. 6 points
PARTIE A
Une société souhaite exploiter un nouveau détecteur qui permet de
mesurer la désintégration de noyaux radioactifs. Pour tester ce
détecteur, la société l’utilise pour déterminer le nombre de noyaux
radioactifs présents dans un échantillon radioactif à des instants
donnés. Voici les résultats des relevés réalisés au cours des heures
qui ont suivi le début du test :
Nombre
ti d’heures écoulées depuis
le début du test
|
0
|
2
|
4
|
6
|
8
|
10
|
Nombre
de noyaux Ni détecté dans l’échantillon (enmilliards)
|
500
|
440
|
395
|
362
|
316
|
279
|
1. a. Recopier et compléter la deuxième
ligne du tableau ci-dessous ¡on arrondira les valeurs à 10 −3
:
ti
|
0
|
2
|
4
|
6
|
8
|
10
|
yi
= ln Ni
|
ln
500 ~6,215
|
ln
440 ~6,087
|
5,979
|
5,892
|
5,756
|
5,631
|
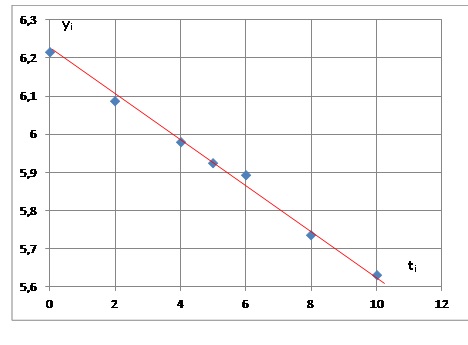
b. Représenter le
nuage de points de coordonnées (t i ; y i ).
c. Un ajustement
affine est-il envisageable ? Pourquoi ?
Le nuage de points semble s'organiser autour d'une droite. Un
ajustement affine est donc envisageable.
d. À l’aide de la
calculatrice, déterminer une équation de la droite D d’ajustement de y
en t par la méthode des moindres carrés sous la forme y = at +b, où les
coefficients a et b seront arrondis à 10 −3.
e. Tracer alors la
droite D.
y = -0,058 t +6,213.
 2. a
2. a. On choisit la
droite D comme modèle d’ajustement du nuage de points Mi (t i
; y i ).
À l’aide de la question 1d, montrer alors que, pour tout réel t positif
ou nul, le nombre de noyaux, en milliards, détectés dans l’échantillon
au bout de t heures écoulées depuis le début du test, est de la forme :
Ae Bt où A (arrondi à l’unité) et B (arrondi au millième)
sont deux réels à préciser.
ln N = -0,058 t +6,213 ; N = exp(-0,058 t +6,213 );
N = exp(-0,058t) x exp(6,213) ; N =
499 exp(-0,058t).
b. La loi de
désintégration assure que la fonction f , qui à tout réel t positif ou
nul, associe le nombre de noyaux, en milliards, présents dans
l’échantillon au bout de t heures, est définie par f (t ) = 500e −0,06t
. Le test réalisé doit-il conduire la société à exploiter le nouveau
détecteur ? Pourquoi ?
Au bout de 10 heures, l'écart entre les deux modèles est inférieur à 2
%.
500 x e -0,6 ~274 ; (279-274) / 274 x100 ~1,8 %.
Le nouveu dtecteur est exploitable.
|
....
...
|
PARTIE
B
On étudie à présent la fonction f définie sur [0, +∞[ par f (t ) = 500e−0,06t
.
1. On admet que la
limite de e-0,06t est égale à zéro quand t tend vers
l'infini.
Déterminer et interpréter graphiquement la limite de f en +∞.
La droite d'équation y = 0 est asymptote à la courbe représentative de
la fonction f(t).
2. Calculer f ′(t )
où f ′ est la fonction dérivée de f .
f '(t) = 500 x(-0,06 )e-0,06t = -30 e-0,06t.
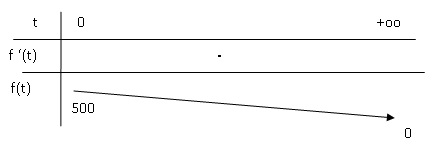
3. En déduire le
tableau de variations de la fonction f .
e-0,06t étant positif, f '(t) est négative et f(t) est
strictement décroissante.
4. On rappelle que
f (t ) est le nombre de noyaux, en milliards, présents dans
l’échantillon radioactif
t heures après le début du test.
a. Calculer le
nombre de noyaux présents dans l’échantillon 24 heures après le début
du test.
On arrondira à l’unité.
500 x e(-0,06x24) =118,46 ~118
milliards.
b. Au bout de
combien d’heures la moitié des noyaux présents dans l’échantillon au
début du
test aura-t-elle disparu ? On justifiera la réponse par un calcul et on
arrondira à l’heure.
250 = 500 e-0,06t ; 0,5 = e-0,06t ; ln 0,5 =
-0,06 t ; t = -ln0,5 / 0,06 ; t ~11,55 soit 12 h.
Exercice 2 ( 6
points ).
On s’intéresse à une modélisation de la concentration d’un médicament,
injecté dans le sang d’un patient, en fonction du temps.
À 7 heures du matin, on injecte le médicament au patient. Toutes les
heures, on relève la concentration de médicament dans le sang, exprimée
en μg·mL−1. À l’injection, cette concentration est égale à
3,4μg·mL−1.
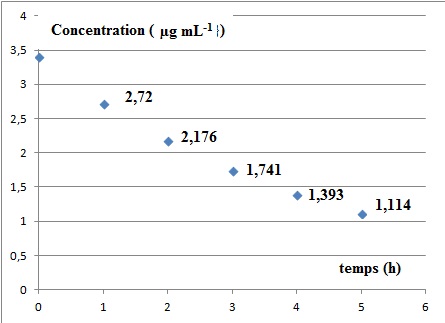
Le nuage de points ci-dessous donne la concentration de ce médicament
dans le sang en fonction du temps écoulé depuis l’injection.
PARTIE A
Dans cette partie, on modélise la concentration de ce médicament par
une fonction définie sur l’intervalle [0 ; 5].
Parmi les troismodélisations proposées, une seule est correcte.
Laquelle ? Justifier.
a) f : f(x)= 0,6x +3,4
b) g(x)= 3,4e−0,223x
c) h(x)=9 / (3+x).
h(x) ne convient pas car h(0) = 3, diffère de 3,4.
f(x) ne convient pas car cette fonction affine est strictement
croissante.
g(x) convient., fonction strictement décroissante et g(5) ~1,1.
|
|
|
On administre à un patient un médicament par voie
PARTIE B
Dans cette partie, on choisit de modéliser la concentration du
médicament par une suite, en prenant, pour valeurs des trois premiers
termes de la suite, les valeurs données par le graphique placé avant la
partie A.
1. Pour tout
entier naturel n, on note Cn la concentration, exprimée en
μg·mL−1, au bout de n
heures, de ce médicament dans le sang. Une partie de ce médicament est
éliminée toutes les
heures.
a. Par lecture du
graphique, donner les valeurs de C0, C1 et C2.
C0 = 3,4 ; C1 = 2,72 ; C2 = 2,176.
b. Que peut-on
alors conjecturer sur la nature de la suite (Cn) ? Pourquoi ?
La suite (Cn) est décroissante et converge vers zéro.
On admet qu’à chaque heure, la concentration du médicament restante
baisse de 20%.
2. Pour tout entier
naturel n, exprimer Cn en fonction de n.
Suite géométrique de raison 1-0,2 = 0,8 et de premier terme 3,4.
Cn =
3,4 x 0,8n.
3. Déterminer alors
la limite de la suite (Cn) lorsque n tend vers l’infini.
Interpréter cette limite dans
le contexte de l’exercice.
0 <0,8 < 1, 0,8n tend vers zéro si n tend vers
l'infini.
Au bout d'un temps suffisamment long, l'organisme a éliminé tout le
médicament.
4. Soit
l’algorithme suivant :
Variables :
n entier naturel
C réel
Initialisation
:
Affecter à n la valeur 0
Affecter à C la valeur 3,4
Traitement
:
Tant que C est supérieur à 1
Affecter à n la valeur n +1
Affecter à C la valeur 0,8×C
Fin tant que
Sortie :
Afficher n.
Quelle valeur affiche l’algorithme ? Interpréter le résultat dans le
contexte de cet exercice.
L'algorithme affiche la durée ( en heure ) au bout de laquelle la
concentration du médicament devient inférieure à 1 µg mL-1.
5. Pour des
raisons
d’efficacité, le patient reçoit immédiatement une nouvelle injection de
médicament dès que, lors d’un relevé à une heure donnée, la
concentration c du médicament dans le sang est inférieure ou égale à
1μg·mL−1. À la nouvelle injection, la concentration du
médicament
dans le sang est alors égale à c+3,4 μg·mL−1.
a. À quelle heure
le patient devra-t-il recevoir une deuxième injection?
3,4 x 0,8n <
1 ; 0,8n <
1 / 3,4 ; n ln 0,8 < ln
(1/3,4) ;
n >5,484 ; n = 6 ; 7 + 6 = 13
heures.
b. Quelle est la concentration du
médicament à cette deuxième injection ?
On arrondira le résultat à 0,1μg·mL−1.
c=3,4
x 0,86 =0,891 ~0,9 mg mL-1.
c. À quelle heure
le patient devra-t-il recevoir une troisième injection ?
(0,9 +3,4) x0,8n <0,1 ; n ln0,8 < ln(1 / 4,3) ; n
>6,53 ; n ~7 ; 13 +7 = 20
heures.
|
|
|
|
EXERCICE 3 4 points
La
Direction de la recherche, des études, de l’évaluation et des
statistiques (Drees) affirme qu’en France : 7 adultes sur 10 portent
des lunettes.
On prélève au hasard un échantillon de 40 adultes parmi la population
française. On assimile ce prélèvement à un tirage avec remise.
Soit X la variable aléatoire qui, à tout échantillon de ce type,
associe le nombre de porteurs de lunettes dans l’échantillon.
1. a. Montrer que X
suit une loi binomiale dont on précisera les paramètres.
Les
prélevements sont indépendants et leur nombre est fixé à n = 40. La
probabilité qu'une personne porte des lunettes est constante p = 0,7.
La probabilité qu'une personne ne porte pas de lunettes est q =
1-p = 0,3.
b. Calculer la
probabilité qu’il y ait au moins 30 porteurs de lunettes dans un tel
échantillon de 40 adultes. On donnera la valeur arrondie à 10−3.
p(X >30) = 1 -P(X <30)=1-0,804=0,196.
On admet que la loi binomiale de la variable aléatoire X précédente
peut être approchée par une loi normale de paramètres μ et s.
2. On a représenté
ci-dessous un diagramme en bâtons et une courbe C. L’une de ces deux
représentations est la représentation de la loi binomiale suivie par X
; l’autre celle de la loi normale de paramètres μ et s.
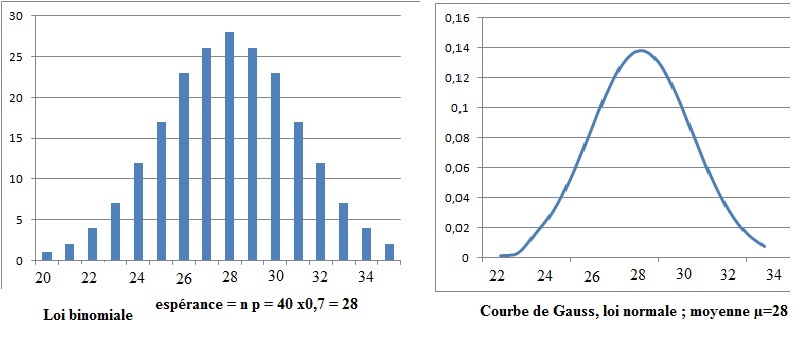
On affirme que l’écart type s
de la loi normale est égal à 8. Cette affirmation est-elle correcte ?
Pourquoi ?
n =40 ; p = 0,7 ; q = 1-p = 0,3.
s =
(npq)½ = (40 x0,7 x0,3)½ =2,9, différent de 8.
3. a. Déterminer un
intervalle de fluctuation asymptotique à 95% de la fréquence des
porteurs de lunettes dans un échantillon aléatoire de 40 adultes en
France. On arrondira les bornes de l’intervalle à 10−3.
1,96 (pq / n)½ =1,96 x(0,7 x0,3 / 40)½ =0,07246.
Intervalle de fluctuation [ 0,7 -0,07246 ; 0,7 +0,07246] soit [0,628 ;
.0,772 ].
b. Dans un
échantillon de 40 adultes en France, on compte 24 porteurs de lunettes.
Déduire de la question précédente si cet échantillon remet en cause
l’affirmation de la Drees qui figure au début de l’exercice.
24 / 40 = 0,6 ; cette valeur est en dehors de l'intervalle précédent.
Cet échantillon remet en cause l'affirmation du début.
|
Exercice 4.
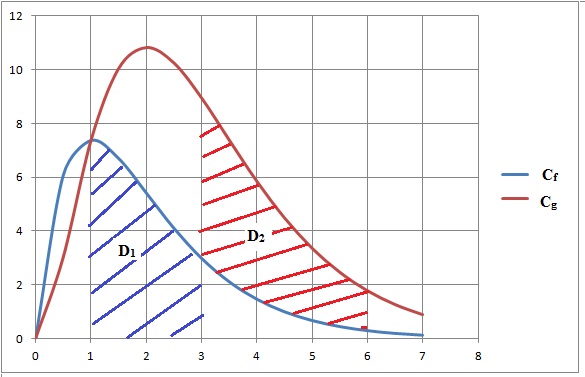
Soient les fonctions f et g définies sur [0 ; 7] par
f (x) = 20xe−x et g (x) = 20x2e−x .
On note Cf et Cg les courbes représentatives
respectives des fonctions f et g représentées ci-dessous.
1. On note :
• D1 l’aire du domaine délimité par la courbe Cf
, l’axe des abscisses et les droites d’équations x = 1 et x = 3 ;
• D2 l’aire du domaine délimité par les courbes Cg
, Cf et les droites d’équation x = 3 et x = 6.
a. Hachurer les
domaines Dl et D2 sur le graphique donné.
b. Encadrer, par
deux entiers consécutifs, les aires, en unités d’aire, des domaines D1
et D2.
D1 est comprise entre 10 et 11 unités d'aire.
D2
est comprise entre 10 et 11 unités d'aire.
2. La commande Int ( f (x),x,a,b)
d’un logiciel de calcul formel permet de calculer la valeur des
l’intégrales.
On obtient alors les résultats suivants pour quatre intégrales :
1 : Int(20xe-x,x,1,2) ; 40e-1-60e-2.
2 :
Int(20xe-x,x,2,3) ; 60e-2-80e-3.
3 :
Int(20xe-x,x,3,6) ; 80e-3-140e-6.
4 :
Int(20x2e-x,x,3,6) ; 340e-3-1000e-6.
a. Déterminer les
aires des domaines D1 et D2 en justifiant la
réponse. On donnera les valeurs exactes.
D1
: 40e-1-60e-2+ 60e-2-80e-3= 40e-1-80e-3~10,73.
D2 : 340e-3-1000e-6-(80e-3-140e-6)=260e-3-860e-6~10,81.
b. Comparer les valeurs des deux
aires obtenues.
D2 est supérieure à D1.
|
|