Mathématiques,
bac
STL biotechnologies Antilles 2017.
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice 1. 4 points
Dans
cet exercice, on s’intéresse à l’indice demasse corporelle (poids en kg
divisé par le carré de la taille en m), noté IMC, de personnes adultes,
âgées de 18 à 74 ans.
Une personne est considérée «maigre » si son IMC est inférieur à 18,5.
Elle est considérée « de poids normal » si son IMC est compris entre
18,5 et 25.
Elle est considérée « en surpoids » si son IMC est compris entre 25 et
30.
Elle est considérée « obèse » si son IMC est supérieur à 30.
Les probabilités seront arrondies à 10−3.
1. On note X la
variable aléatoire qui, à une personne adulte prise au hasard, associe
son IMC. Dans cette question, on suppose que X suit la loi normale
d’espérance 24,9 et d’écart type 5,3. On prend une personne au hasard
dans la population.
a. Déterminer la
probabilité que cette personne soit« en surpoids ».
P(X <30)=0,83204 ;
P(X <25)=0,507526 ;
P(25 < X < 30)=0,83204-0,507526 ~0,325.
b. Déterminer la
probabilité que cette personne soit «maigre ».
P(X < 18,5)
=0,1136 ~0,114.
2. On suppose qu’en
France, la proportion d’adultes obèses est de 15%.
a. Déterminer
l’intervalle de fluctuation asymptotique au seuil de 95% de la
fréquence de personnes
obèses dans un échantillon de taille 800. Arrondir les bornes de
l’intervalle à 10−3.
n
= 800, supérieur à 30 ; np = 800 x 0,15 = 120, supérieur à 5 ; n(1-p) =
800 x0,85=680, supérieur à 5. Les conditions sont requises pour
déterminer un intervalle de fluctuation asymptotique à 95 %.
1,96 x(px(1-p) / n )½ = 1,96 x(0,15 x0,85 / 800)½=1,96
x0,012624 ~0,025.
Intervalle de fluctuation [0,15-0,025 ; 0,15 +0,025] soit [0,125 ;
0,175].
b. Dans le cadre
d’un plan de prévention planifié par une région française, une agence
de santé
indépendante a réalisé une enquête au cours de laquelle a été mesuré
l’IMC de 800 personnes
adultes habitant cette région. Parmi celles-ci, 148 ont un IMC
supérieur à 30.
Peut-on considérer que la population de cette région comporte une
proportion d’adultes
obèses conforme à la moyenne nationale ou, au contraire, qu’il y a lieu
d’envisager des actions
de prévention contre l’obésité ? Justifier la réponse.
148 / 800 ~0,185.
0,185 est en dehors de l'intervalle [0,125 ; 0,175] ; 0,185 > 0,175.
Il y a
lieu d’envisager des actions de prévention contre l’obésité.
|
....
...
|
Exercice 2.
QCM 4 points.
1. On injecte à un
patient une dose de 5 mL d’une solution antibiotique, ce qui correspond
à une
dose de 5 mg d’antibiotique. La quantité d’antibiotique présente dans
le sang diminue chaque
heure de 5,5%.
Au bout de combien d’heures révolues la quantité de médicament restant
dans le sang sera-t- elle
passée sous le seuil des 20% de la quantité injectée au départ du
traitement ?
a. 9 ; b. 28 ; c. 57; d. 29.
un =5 x(1-0,055)n= 5 x0,945n.
5 x0,945n < 0,2 x5 ; 0,945n < 0,2 ; n ln(0,945)
< ln (0,2) ;
n >ln(0,2) / (ln(0,945) ; n >28,45 ; n > 29 heures.
2. Dans un échantillon de 136
personnes prélevé dans la population d’une ville, on observe que 57
d’entre elles portent des lunettes. On appelle p la proportion des
personnes portant des lunettes
dans la population.
L’intervalle de confiance dont les bornes sont arrondies à 10−2,
au niveau 95%, pour la proportion
p est : a. [0,35 ; 0,49] ; b. [0,47 ; 0,67] ; c. [0,41 ; 0,43] ; d.
[0,34 ; 0,50]
f = 57 / 136 = 0,419 ; 1 / n½ = 1 / 136½ =0,0857.
Intervalle de confiance [ 0,419 -0,0857 ; 0,419 +0,0857 ) soit [0,34 ; 0,50].
3. Une variable
aléatoire Y suit une loi exponentielle de paramètre 3,5.
La probabilité P(0,4<Y
<0,8),
approchée à 0,001 près, est égale à :
a. 0,186 ; b. 0,650 ; c. 0,734 ; d. 0,286.
P(Y < 0,4) =
1-exp(-3,5 x0,4) = 1-exp(-1,4)=0,7534 ;
P(Y < 0,8) = 1-exp(-3,5 x0,8) = 1-exp(-2,8)=0,9392 ;
P(0,4<Y <0,8)=0,9392-0,7534 ~0,186.
4. On rappelle que la fonction
ALEA() d’un tableur renvoie un nombre aléatoire compris entre 0 et 1,
et simule une variable aléatoire suivant une loi uniforme sur
l’intervalle [0 ; 1].
On souhaite simuler une variable aléatoire suivant une loi uniforme sur
l’intervalle [-1 ; 1].
Quelle formule faut-il écrire dans le tableur ?
a. = 2×ALEA()−1 ; b. =
(ALEA()+1)÷2 ; c. = 2×ALEA() ; d. = ln(ALEA()
|
|
|
EXERCICE
3 4 points
On administre à un patient un médicament par voie
intraveineuse. Ainsi la concentration du produit
actif est quasi immédiatement maximale après l’injection, puis elle
diminue de 3% par minute.
On notera C0 la concentration à l’instant t = 0 minute et Cn
la concentration en mg. L−1 au bout de n
minutes. On pose C0 = 1.
1. Justifier que la
suite (Cn) est géométrique. Préciser sa raison.
On passe d'un terme au suivant en le multipliant par 1-0,03 = 0,97.
(Cn) est une suite géométrique de raison 0,97 et de premier
terme C0 = 1.
2. Exprimer Cn
en fonction de n.
Cn = C0 x0,97n = 0,97n.
3. En résolvant une
inéquation, déterminer à partir de quelle valeur de n la concentration
du produit
actif aura diminué de moitié.
0,97n <
0,5 ; n x ln(0,97) < ln
(0,5) ; n x(-0,03046) >
(-0,6931) ; n >
22,75 ; n > 23 minutes.
4. On considère le
premier algorithme suivant :
Variables : K est un nombre réel
Initialisation : K prend la valeur 1
Traitement : Répéter 5 fois
K prend la valeur 0,97∗K
Sortie : Afficher K
a. Quelle est la
valeur K affichée à l’issue de l’exécution de cet algorithme ? On
arrondira à 0,000 1.
0,975 ~0,8587.
b. Quelle
interprétation peut-on donner de cette valeur de K en terme de
concentration du médicament ?
Cinq minutes après l'injection, la concentration du médicament dans le
sang est égale à 0,8587 mg L-1.
5. On considère
maintenant l’algorithme suivant :
Variables : i est un entier naturel, K est un nombre réel
Initialisation : K prend la valeur 1
i prend la valeur 0
Traitement : Tant que K > 0,5
i prend la valeur i +1
K prend la valeur 0,97∗K
Sortie : Afficher i
a. Expliquer
pourquoi cet algorithme exécutera plus de 5 itérations de la boucle«
Tant que ».
b. Quel résultat
l’exécution de cet algorithme permet-elle de retrouver ?
La boucle Tant que s'exécute tant que K est supérieur à 0,5. Or K ~0,86
lorsque i est égal à 5.
Cette boucle s'effectue plus de 5 fois.
Cet algorithme donne la durée en minute, à partir de laquelle la
concentration a diminué de moitié.
|
|
|
|
EXERCICE 4 8 points
Partie A - Etude
statistique
Les immunoglobulines G, notées IgG, sont des anticorps qui
interviennent dans l’élimination d’antigènes.
On étudie la concentration d’IgG dans le sang d’un patient au fil des
semaines lors du contact avec un antigène.
On a recueilli les informations consignées dans le tableau suivant, où ti
est le temps en semaines écoulées après ce contact et yi le
taux d’immunoglobuline G en g. L−1 :
1. Compléter la
troisième ligne du tableau suivant, les résultats seront arrondis à 10−2
:
ti
|
1
|
2
|
3
|
4
|
5
|
6
|
yi
|
13,4
|
14,7
|
13,9
|
12,8
|
11,7
|
10,5
|
z
= ln(y / t)
|
2,60
|
1,99
|
1,53
|
1,16
|
0,85
|
0,56
|
2. Donner, à
l’aide
de la calculatrice, l’équation de la droite de régression linéaire de z
en t , obtenue par la méthode des moindres carrés. Les coefficients
seront arrondis à 10−2 près.
z= -0,40t +2,85.
3. Déterminer un
ajustement de y en fonction de t de la forme y = atebt où a
et b sont des nombres réels. On arrondira les a et b au dixième.
y / t = exp(-0,40t +2,85) = exp(-0,40t) +exp(2,85) = 17,3e-0,4t
; y =17,3 t exp-0,4t.
4. Estimer le taux
d’IgG à la 8e semaine à l’aide de l’expression de la
question 3. Arrondir à 10−1.
y = 17,3 x8 x e-3,2 ~5,6
g L-1.
|
PARTIE B.
Etude d'une fonction.
Soit f la fonction
définie sur [0 ; +∞[ par f (t )= 17,3te−0,4t .
On note Cf la courbe représentative de la fonction f dans un
repère.
1. On donne :
limite de f(t) à l'infini = 0. Interpréter graphiquement ce résultat.
La droite d'équation y = 0 est
asymptote à la courbe.
2. On note f ′ la
dérivée de f sur [0 ; +∞[. Montrer que pour tout t de [0 ; +∞[, f ′(t )
= (17,3−6,92t )e−0,4t .
3. a. Étudier le
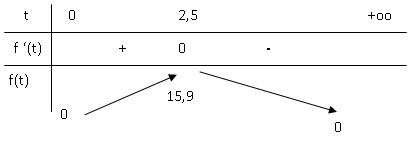
signe de f ′(t ) sur [0 ; +∞[.
b. Établir le
tableau de variations de f sur [0 ; +∞[.
On pose u = 17,3 t et v = e-0,4t ; u' = 17,3 ; v' = -0,4 e-0,4t.
f ' = u'v +v'u = 17,3 e-0,4t -0,4 x17,3te-0,4t =
(17,3 -6,92t)e-0,4t.
e-0,4t
étant positif, le signe de f '(t) est celui de 17,3 -6,92t.
f '(t) < 0 si t >2,5 ; f '(t) >0 si t < 2,5 et
f '(t) = 0 si t =2,5.
c. Soit F la fonction définie sur [0
; +∞[ par F(t )= (−108,125−43,25t )e−0,4t .
Montrer que F est une primitive de f sur [0 ; +∞[.
Dériver F en posant u = (−108,125−43,25t et v =
e-0,4t ; u' = -43,25 ; v' = -0,4 e-0,4t.
F ' = u'v +v'u = -43,25 e-0,4t +0,4 x(108,125+43,25t)e-0,4t
= 17,3t e-0,4t= f(t).
4. Calculer la valeur moyenne de f
sur l’intervalle [1 ; 5]. On donnera la valeur approchée arrondie à 10−1
près.
Vm = 1 / (5-1) (F(5) -F(1)).
F(5) = (-108,125 -43,25 x 5) e-2 ~ -324,375 x 0,135~ -43,9.
F(1) =
(-108,125 -43,25 ) e-0,4 ~ -151,375 x 0,67~ -101,47
Vm = (101,47-43,9) / 4 ~14,4
g L-1.
Partie C.
On suppose que f (t ) représente le taux d’IgG en g.L−1 en
fonction du temps t en semaines (écoulées après contact avec
l’antigène), où la fonction f est celle de la partie B.
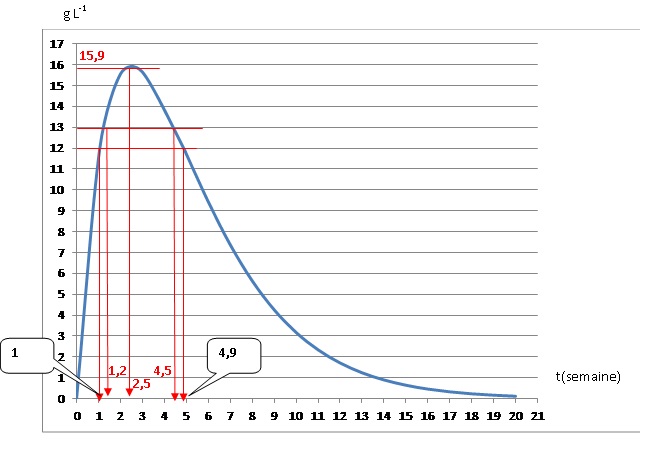
1. Quel est le taux
maximal d’IgG du patient ? Quand ce taux est-il atteint ?
2. Le test
sérologique d’IgG est positif lorsque le taux d’IgG dépasse 13 g.L−1.
Déterminer, à l’aide du graphique, sur quelle période une analyse de
sang donnerait ce test positif.
Entre 1,2 et 4,5 semaines le test est positif.
3. Sachant que le
taux d’immunoglobuline est inférieur à 12 g.L−1 en moyenne
chez un adulte sain, suivant ce modèle, durant quelles périodes le
sujet pourrait-il être diagnostiqué sain ?
Entre 0
et une semaine et au delà de 4,9 semaines, le test est négatif.
|
|