Mathématiques,
suite géométrique, algorithme
Bac Sti2d et Stl 2016.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie juin 2016.
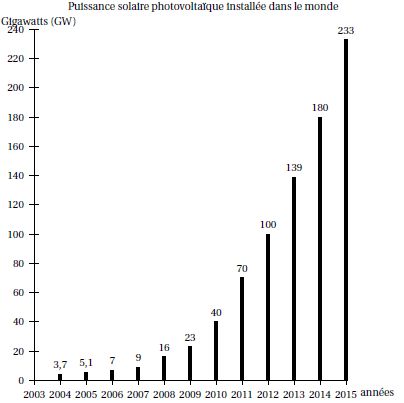
L’énergie photovoltaïque voit son coût baisser de façon importante
depuis plusieurs années, ce qui engendre une croissance forte de ce
secteur. L’évolution de la puissance solaire photovoltaïque installée
dans le monde entre fin 2004 et fin 2015 est résumée dans le graphique
ci-dessous :
 Pn+1
e
1. Calculer les pourcentages
d’augmentation annuels entre 2013 et 2014 ainsi qu’entre 2014 et 2015
(arrondir à 10−1). Pn+1
e
1. Calculer les pourcentages
d’augmentation annuels entre 2013 et 2014 ainsi qu’entre 2014 et 2015
(arrondir à 10−1).
(180-139) / 139 * 100 = 29,5 %
; (233-180)
/ 180 * 100 = 29,4 % .
2.
On se propose d’estimer la puissance solaire photovoltaïque installée
dans le monde dans les 15 ans à venir, si le taux de croissance annuel
reste constant et égal à 30%.
On note Pn la puissance solaire photovoltaïque installée
dans le monde, en GW, à la fin de l’année 2015+n. On a ainsi P0
= 233.
a. Calculer P1
puis P2( arrondir à 10−1).
P1 = P0(1+0,30) = 1,3 P0 = 1,3 *233 =302,9 GW.
P2
= 1,3 P1 = 1,32P0 =1,32
*233 =393,8 GW.
b.
Exprimer Pn+1 en fonction de Pn.
Pn+1 = 1,3 Pn.
En déduire la nature de la suite (Pn)
et donner ses éléments
caractéristiques.
Suite géométrique de raison
1,3 et de premier terme 233.
d. Exprimer Pn
en fonction de n.
Pn =
233 x 1,3n.
e. Calculer la
puissance solaire photovoltaïque, en GW, installée dans
le monde fin 2025 (arrondir à l’unité).
n=10 ; P10 = 233 x 1,310 = 3212 GW.
f. Quel est le
pourcentage global d’augmentation de cette puissance
solaire mondiale entre 2015 et 2025 (arrondir à l’unité) ?
(3212-233) / 233 =12,7854 ( ~1279 %)
3. On
veut déterminer l’année durant laquelle la puissance solaire
photovoltaïque installée dans le monde atteindrait 16 000 GW. Pour
atteindre cette puissance, les panneaux photovoltaïques occuperaient au
sol
l’équivalent d’un carré de 400 km de côté et suffiraient pour produire
toute l’électricité
consommée dans le monde (consommation domestique, industrielle et des
transports.
a. On considère
l’algorithme ci-dessous.
Recopier et compléter les lignes 3 et 7 afin que cet algorithme réponde
à la question posée.
1/ Affecter à N la valeur 0
2/ Affecter à P la valeur 233
3/ Tant que P<16000
4/ Affecter à N la valeur N +1
5/ Affecter à P la valeur P ×1,30
6/ Fin Tant que
7/ Afficher N +2015.
N
|
15
|
16
|
17
|
P
|
233
x1,315=11926
|
233
x1,316=15504
|
233
x1,317=20155
|
P
<16000
|
Faux
|
Faux
|
Vrai
|
b. En
faisant tourner cet algorithme complété, déterminer l’année durant
laquelle la puissance solaire photovoltaïque installée dans le monde
dépasserait 16 000 GW.
c. Proposer une
autre méthode, directe et non algorithmique, pour répondre à la
question précédente en détaillant la démarche utilisée.
233
x 1,3x >16000 ; 1,3x
>16000 / 233 ; 1,3x
>68,67 ; x log1,3 > log 68,67 ; x > 16,1 ; x
>17.
x > 17 ; année 2015+17 = 2032.
|
|
|
Métropole septembre 2016.
Dans
une municipalité, la collecte des déchets des particuliers s’effectue,
depuis 2012, à l’aide de camions équipés de capteurs. Une tarification
« incitative » permet aux habitations de diminuer leur facture en
réduisant la masse de leurs ordures ménagères résiduelles par un choix
de produits comportant moins d’emballages, une réduction du gaspillage
alimentaire et un meilleur tri.
Le document 1 présente la masse
moyenne de déchets, en kilogrammes, collectés par année depuis 2012 et
par habitation de la ville.
Le document 2 présente les tarifs
pratiqués en 2015 par la ville pour la collecte des ordures ménagères
résiduelles (on suppose que ces tarifs resteront identiques les années
suivantes).
Année
|
2012
|
2013
|
2014
|
2015
|
Déchets
recyclables
|
261
|
275
|
289
|
305
|
ordures
ménagères résiduelles
|
274
|
269
|
262
|
256
|
| Total |
535 |
544 |
551 |
561 |
| Tranches
tarifaires |
tranche
1 |
Tranche
2 |
Tranche
3 |
| masse
M en kg |
[0
; 100 [ |
[100
; 300[ |
>=300 |
| Forfait |
200
€ |
300
€ |
420
€ |
PARTIE A
1. Commenter
l’évolution de la masse moyenne des déchets collectés par habitation
depuis 2012.
La masse totale des ordures ménagères croît entre 2012 et 2015. Il en
est de même de la masse des déchets recyclés.
2.
Une famille a jeté 320 kg d’ordures ménagères résiduelles en 2015. Si
elle diminue la masse de ses ordures ménagères résiduelles de 1% par
an, en quelle année changera-t-elle de tranche tarifaire ?
m0= 320 ; m1 = 0,99 m0 ; m2 = 0,99 m1 = 0,992
m0 ;
mn = 0,99n m0 ; 0,99n x
320 < 300 ; 0,99n
< 300 / 320 ;
0,99n < 0,9375
;
n log 0,99 < log 0,9375 ; n >= 6,4 ~7 ans soit fin 2022.
PARTIE B.
En 2015, la municipalité comptait 10 000 habitations.
Dans
le cadre de l’aménagement d’un nouveau quartier un constructeur
garantit la livraison de 300 nouvelles habitations chaque année au 1er
janvier, de 2016 à 2024. En raison de la demande, ces logements seront
immédiatement occupés dès le 1er janvier.
La municipalité
a souscrit avec un centre d’incinération un contrat de 9 ans qui a pris
effet au 1er janvier 2016. Le contrat prévoit de fortes pénalités
financières dès que la masse annuelle d’ordures ménagères résiduelles à
incinérer vient à dépasser 2 800 tonnes.
L’objectif de la municipalité est d’éviter ces pénalités.
1. Vérifier
que cet objectif ne sera pas atteint si la masse annuelle moyenne
d’ordures ménagères résiduelles par habitation reste constante égale à
256 kg.
0,256 x 10 000 + 8 x 300 x 0,256 =2560+ 614,4 =3174,4 tonnes.
2.
Afin d’atteindre cet objectif, il convient donc de diminuer la masse
moyenne d’ordures ménagères résiduelles à incinérer. La municipalité
souhaite déterminer le pourcentage annuel minimal de réduction de la
masse moyenne d’ordures ménagères résiduelles par habitation, pendant
toute la durée du contrat.
On admet que l’algorithme ci-dessous détermine ce pourcentage.
Variables
N : un nombre entier
m : un nombre réel
q : un nombre réel
Initialisation
q prend la valeur 1
N prend la valeur 12 700
m prend la valeur 0,256
Traitement
Tant que N ×m >=2800
q prend la valeur q −0,001
m prend la valeur 0,256×q9
Fin Tant que
Sortie
Afficher (1−q)×100
Cet algorithme affiche 1,7.
a. Expliquer la
ligne « N prend la valeur 12 700 »
Nombre d'habitations en 2024 : 10 000 + 9 x 300 = 12 700.
b. Expliquer la
ligne «m prend la valeur 0,256×q9 »
Chaque année la masse moyenne anuelle d'ordure ménagères par habitation
diminue de x %.
La raison de la suite géométrique est q = 1 -x/100.
Au bout de 9 années, la masse d'ordure ménagère par habitation devra
être égale à 0,256 x q9 tonnes..
3.
On considère que la masse annuelle moyenne d’ordures ménagères
résiduelles par habitation va baisser chaque année de 1,7%, à partir du
1er janvier 2016 sur une période de 9 ans.
On note un cette masse, exprimée en tonnes, pour l’année
2015+n où n est un entier naturel. On a donc u0 = 0,256.
a. Calculer les
termes u1, u2 et vérifier que. u3 ≈
0,243. Interpréter u3.
q = 1-0,017 =0,983 ; u1 = 0,256 x 0,983 = 0,251648 ~0,252 t.
u2
= 0,251486 x 0,983 =0,24737 ~0,247 t.
u3 =0,24737 x 0,983 ~0,243 t.
Au premier janvier 2019, la mase moyenne annuelle d'ordures résiduelles
par habitation sera de 0,243 t.
b. Quelle est la nature de la suite
(un) ?
Un est une suite géométrique de raison q = 0,983 et de
premier terme u0 = 0,256 t.
c. Exprimer un
en fonction de n.
un = 0,256 x qn.
d. Vérifier que
l’objectif fixé par la municipalité est atteint en fin de 2024.
u9 = 0,256 x 0,9839 =0,219 t.
0,219 *12700 = 2786 t, valeur inférieure à 2800 t ; le contrat
est respecté sans pénalités.
PARTIE C.
Dans cette partie, tous les résultats demandés seront arrondis à 10−3.
Des contrôles sont effectués afin de vérifier le tri des déchets.
Protocole d’étude.
On
choisit au hasard 100 habitations.Des personnels ont ouvert les
poubelles de déchets recyclables de ces habitations afin de déterminer
s’ils étaient conformes (absence de matériaux non recyclables, de
cartons souillés . . . ).
Résultats de l’étude.
Parmi ces 100 poubelles de déchets recyclables, 7 ont été jugées non
conformes.
1.
Déterminer, à l’aide d’un intervalle de confiance avec un niveau de
confiance de 95%, une estimation de la proportion de poubelles de
déchets recyclables qui ne sont pas conformes.
n = 100 ; p = 0,07 ; q = 1-p = 0,93 ; écart type : (pq / n)½
= (0,07*0,93 / 100)½ = 0,0255 ;
intervalle de confiance [ 0,07 -0,0255 x 1,96 ; 0,07 +0,0255 x 1,96 ]
soit [0,02 ; 0,12 ].
2.
La proportion de poubelles de déchets recyclables qui ne sont pas
conformes est-elle nécessairement comprise dans cet intervalle de
confiance ?
Non, le niveau de confiance n'est que de 95 %. Le risque d'erreur est
de 5%.
|
|
|
|
Métropole 06 / 2016.
Un centre de vacances possède une piscine de 600 m3
soit 600 000 litres. L’eau du bassin contient du chlore qui joue le
rôle de désinfectant. Toutefois le chlore se dégrade et 25% de celui-ci
disparaît chaque jour, en particulier sous l’effet des ultraviolets et
de l’évaporation. Le 31 mai à 9 h, le responsable analyse l’eau du
bassin à l’aide d’un kit distribué par un magasin spécialisé.
Le taux de chlore disponible dans l’eau est alors de 1,25 mg/L
(milligrammes par litre).
À partir du 1er
juin pour compenser la perte en chlore, la personne responsable de
l’entretien ajoute, chaque matin à 9 h, 570 g de chlore dans la
piscine. Pour le bien-être et la sécurité des usagers, le responsable
souhaite savoir si cet apport journalier en chlore permettra de
maintenir une eau qui respecte la réglementation : taux de chlore
compris entre 2 mg /L et 4 mg /L.
Partie A.
1. Pour tout entier
naturel n on note un
la quantité de chlore disponible, exprimée en grammes, présente dans
l’eau du bassin le n-ième jour suivant le jour de l’analyse,
immédiatement après l’ajout de chlore. Ainsi u0 est la
quantité de chlore le 31 mai à 9 h et u1 est la quantité de
chlore le 1er juin à 9 h après l’ajout de chlore.
a. Montrer que la
quantité de chlore, en grammes, présente dans l’eau du bassin le 31mai
à 9h est u0 = 750.
1,25 10-3 x 600 000 = 750 g.
Au regard des recommandations de l’agence régionale de santé, le
responsable pouvait-il donner l’accès à la piscine le 31mai ?
Non 1,25 mg/L n'appartient pas à l'intervalle [2 mg /L ; 4 mg /L ].
Il y a sous-chloration, risque de prolifération bactérienne dans l'eau.
b. Montrer que u1
= 1132,5.
25 % du chlore disparait chaque jour ; avant l'ajout, le 1er juin ,il
reste 750 *0,75 =562,5 g de chlore.
Après l'ajout, le 1er juin à 9 h : 570 +562,5 = 1132,5 g.
c. Justifier que
pour tout entier naturel n, un+1 = 0,75un +570.
u1 = 570 +750 x 0,75 = 570 +0,75 u0.
u2 = 570 +0,75 u1 ; u3 = 570
+0,75 u2 ; un = 570 +0,75 un-1
; un+1 = 570 +0,75 un .
d. La suite (un)
est-elle géométrique ?
Non un+1 n'est pas de la forme un+1 = q un
avec q, nombre réel.
2. Soit
l’algorithme ci-dessous :
Variables u : un nombre réel
N : un nombre entier naturel
k : un nombre entier naturel
Initialisation : Saisir la valeur de N
u prend la valeur 750
Traitement : Pour k allant de 1 à N
u prend la valeur 0,75u +570
Fin du Pour
Sortie : Afficher u
a. Quel est le rôle
de cet algorithme ?
Cet algorithme calcule la quantité de chlore disponible, exprimée
en grammes, présente dans
l’eau du bassin le n-ième jour suivant le jour de l’analyse,
immédiatement après l’ajout de chlore.
b. Recopier et
compléter le tableau suivant, par des valeurs exactes, en
exécutant cet algorithme « pas à pas »pour N = 3.
| Variable |
Initialisation |
Etape
1 |
Etape
2 |
Etape
3 |
| u |
750 |
1132,5 |
1419,375 |
1634,53125 |
Etape 2 : 1132,5 *0,75 +570 =1419,375 g ou 1419,4 / 600=2,36 mg/L de
chlore.
Etape 3 : 1419,4 *0,75 +570 =1634,5 g ou 1634,5 / 600=2,72 mg/L de
chlore.
Au regard des recommandations de l’agence régionale de santé, au bout
de combien de jours la piscine peut-elle être ouverte ?
Etape 1 : 1132,5 / 600 = 1,89 mg /L de chlore.
La piscine peut ouvrir le 2 juin.
c. Calculer une
valeur approchée à 10−3 près de la quantité de chlore le 15e
jour juste après l’ajout de chlore. 2264,893 g
| jour |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| mg/L
de chlore |
2,72 |
2,99 |
3,19 |
3,35 |
3,46 |
3,54 |
3,66 |
3,69 |
3,72 |
3,742 |
3,755 |
3,766 |
3,775 |
Partie B.
Au fil du temps, la quantité de chlore évolue. On note dn
l’écart de quantité de chlore d’un jour à l’autre en grammes. Pour tout
entier naturel n, on a dn = un+1 −un.
1. a. Calculer d0,d1
et d2. On donnera une valeur exacte.
d0 = u1 −u0 = 1132,5-750 = 750 x0,75
+570 -750 = 570 -0,25 x 750 =382,5. ( 570 -0,25 u0 )
d1 = u2 −u1 = 1419,375-1132,5 =286,875.
d2 = u3 −u2 = 1634,53125-1419,375
=215,15625.
b. Justifier que d0,d1
et d2 semblent être les termes d’une suite géométrique.
d1 / d0 = 0,75 ; d2 / d1 =
0,75 ; dn+1 = 0,75 dn.
On passe d'un terme au suivant en multipliant ce terme par 0,75.
2. Vérifier que un+1
−un = −0,25un +570.
un+1 =0,75un +570
un+1 -un =0,75un +570-un
=−0,25un +570.
3. On admet que
pour tout entier naturel n, on a dn+1 = 0,75dn .
a. Justifier que dn
= 382,5×0,75n .
d0 =382,5 ; d1 = d0 x 0,75 ; d2
= d1 x 0,75 = d0 x 0,75 x0,75 = 0,752
d0.
d3 =d2 x 0,75 = d0 x 0,752
x 0,75 = 0,753 d0.
b. En déduire que
pour tout entier naturel n, on a un = 2280−1530×0,75n .
dn =un+1-un= 382,5×0,75n .
et un+1 −un = −0,25un +570.
382,5×0,75n = −0,25un +570 ; 0,25un
=570 - 382,5×0,75n ; un = 2280−1530×0,75n.
c. Déterminer la
limite de la suite (un). Interpréter le résultat trouvé.
0,75n tend vers zéro quand n tend vers l'infini. La
limite de la suite est 2280 g de chlore soit 2280 / 600 = 3,8 mg / L.
Cette valeur reste inférieure à 4 mg / L. Il n'y a pas de risque de
surchloration et d'irritation de la peau.
|
|
Antilles Guyanne 2016.
Par
souci de santé, d’environnement ou simplement pour le plaisir du goût,
l’alimentation biologique s’invite de plus en plus dans les assiettes
des français.
Deux fermes auvergnates décident de se convertir dans la production
biologique.
Partie A.
En
2015, la ferme Bernard décide de cultiver 2 hectares selon le mode de
production biologique et d’augmenter cette surface de production de 20%
par an les années suivantes.
On note Sn la surface, en hectare, cultivée selon le mode de
production biologique, durant l’année « 2015 + n ».
1.
Quelle sera la surface cultivée en hectare selon le mode de production
biologique durant l’année 2016, puis durant l’année 2017 ?
S1 =2 x1,2 = 2,4 ; S2
=2,4 x1,2 =,88.
2. Quelle est la nature de la
suite (Sn) ? Justifier.
On passe d'un terme au suivant en multipliant ce terme par 1,2 : suite
géométrique de raison 1,2 et de premier terme 2.
3. Exprimer Sn
en fonction de n.
Sn = 2 x 1,2n.
4. La
ferme Bernard dispose d’une surface de 10 hectares. Durant quelle année
la totalité de la ferme sera cultivée selon le mode de production
biologique ?
10 = 2x 1,2n ; 5 =
1,2n ; log 5 = n log 1,2 ; n =8,82 ~ 9 ( année 2024 ).
Partie
B.
En
2015, la ferme Dupont décide de cultiver 1 hectare, selon le mode de
production biologique et d’augmenter cette surface de 0,8 hectare par
an.
On note un la surface cultivée selon le mode de production
biologique, durant l’année « 2015 + n », exprimée en hectare.
La production biologique impose aux sols un temps de repos pour se
reconstituer.
La
ferme Dupont dispose d’une surface de 18 hectares. Afin de garder un
certain bénéfice, la ferme Dupont limite sa production biologique à 70%
de la surface totale
de la ferme chaque année. On considère l’algorithme suivant :
Variables
K un entier naturel
U un nombre réel
Début
U prend la valeur 1
Pour K allant de 1 à 10
U prend la valeur U +0,8
Fin Pour
Afficher U
Fin.
Tester cet algorithme. Pour cela on recopiera et complétera le tableau
suivant donnant les valeurs de K etU :
| Valeur
de K |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| Valeur
de U |
1,8 |
2,6 |
3,4 |
4,2 |
5 |
5,8 |
6,6 |
7,4 |
8,2 |
9 |
2. Quelle est la
valeur finale affichée par cet algorithme ? À quoi correspond-elle ?
18*0,7 = 12,6, surface maximale cultivée en mode biologique.
Nlle Calédonie.
La politique communautaire de gestion des déchets et ses déclinaisons
françaises sont définies par de nombreuses directives, dont la portée
varie. Certaines ont une portée générale et d’autres concernent
certaines catégories de déchets spécifiques.
Le Projet de Plan national de prévention des déchets 2010−2020 concerne
les déchets ménagers et assimilés (DMA). L’objectif proposé par ce
projet est une réduction annuelle de 7% des DMA produits par habitant
entre 2010 et 2020.
Les DMA produits en France ont été de 590 kg par habitant en 2011 et de
570 kg par habitant en 2013.
Source ADEME
Partie A :
La réduction des DMA produits entre 2011 et 2013 atteint-elle
l’objectif fixé par le Projet de Plan national de prévention des
déchets ?
En 2012 : 590 x0,93 = 548,7 kg par habitant ; en 2013 : 548,7 x0,93
=510,3 kg par habitant.
L'objectif n'a pas été atteint : 570 >510,3.
Partie B :
On considère que les objectifs du plan national de prévention des
déchets sont atteints à partir de 2013. On modélise par une suite (un)
la quantité de DMA produits en kg par habitant, le terme un
correspondant à l’année (2013+n). Ainsi u0 = 570.
1. Calculer u1.
u1 = 0,93 u0 = 0,93 x570 =530,1.
2. Quelle est la
quantité de DMA produits, arrondie au kg par habitant, en 2015 ?
n=2 ; u2=0,93 u1 = 0,93 x530,1 ~493.
3. Déterminer la
nature de la suite (un) puis exprimer un en fonction de n.
On passe d'un terme au suivant
en multipliant ce terme par 0,93 : suite géométrique de raison 0,93 et
de premier terme 570.
un = 0,93n u0 = 570 x0,93n.
Partie C :
On considère l’algorithme suivant :
Variables
n : un nombre entier naturel
q : un nombre réel
U : un nombre réel
Entrée
Saisir n
Initialisation
Affecter à u la valeur 570
Affecter à q la valeur 0,93
Traitement
Répéter n fois
Affecter à u la valeur u ×q
Sortie
Afficher u
1. On entre dans
l’algorithme la valeur n = 4.
Faire fonctionner cet algorithme pour compléter les cases non grisées
du tableau suivant, que l’on recopiera (on donnera des valeurs
arrondies au kg près par habitant).
|
n
|
q
|
u
|
Entrée
et initialisation
|
4
|
0,93
|
570
|
1er
passage dans la boucle
|
|
570x0,93~530
|
| 2è
passage dans la boucle |
530,1
x0,93 ~493
|
| 3è
passage dans la boucle |
493
x0,93 ~459
|
| 4è
passage dans la boucle |
458,48
x0,93 ~426
|
2.
Interpréter la valeur de u obtenue au quatrième passage dans la boucle
de l’algorithme.
En 2017, chaque habitant produit annuellement 426 kg de DMA.
3. Quel sera le
pourcentage de réduction des DMA produits entre 2013 et 2017 si
l’objectif du Projet de Plan national de prévention des déchets est
atteint chaque année ?
(570-426) / 570 x100 ~25,3 %.
4. Quelle devrait
être la quantité de DMA produits en 2020 pour atteindre l’objectif fixé
par le Projet de Plan national de prévention des déchets ?
n = 7 ; u7 = 570 x0,937 ~343.
|
|