Mathématiques,
étude de fonctions
Bac Sti2d et Stl 2016.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie juin 2016.
Partie A : Lecture
graphique
On considère la courbe C associée à une fonction f représentée avec la
droite T, tangente à la courbe C au point d’abscisse 0.
1. Résoudre graphiquement sur l’intervalle [−1 ; 1,5] et avec la
précision permise par le dessin les deux inéquations suivantes :
a. f (x) supérieure
ou égale à 1.
b. f ′(x) supérieure ou égale à 0.
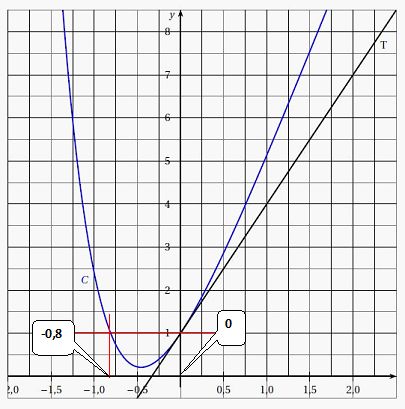
f (x) est supérieure
ou égale à 1 pour x appartenant à [-1 ; -0,8 ] et pour x
appartenant à [0 ; 1,5 ].
f ′(x) est supérieure ou égale à 0 pour x appartenant à
l'intervalle [-0,5 ; 1,5 ] ( fonction croissante ).
2. a.
Donner l’équation de la tangente T à la courbe C au point de
coordonnées (0 ; 1) en sachant que cette tangente passe par le point de
coordonnées (2 ; 7).
y = a x+b avec a et b des constantes.
1 = 0 x+b soit b = 1 et 7 = 2a +1 soit a = 3. y = 3x+1.
b. En déduire le
nombre dérivé f ′(0).
f'(0) = 3,
coeficient directeur de la tangente à la courbe au point d'abscisse x=0.
Partie B : Étude de
la fonction f
Soit f la fonction définie sur R par la relation f (x) = e−2x
+5x.
1. Déterminer, en
la justifiant, la limite de f en +oo.
Le terme en exponentielle tend vers zéro lorsque x tend vers l'infini.
f(x) tend vers l'infini lorsque x tend vers l'infini.
On admet pour la suite que la limite de f en −oo est +oo.
2. Calculer f ′(x)
et étudier son signe sur R.
f '(x) = -2 e-2x +5.
f '(x) =0 ; e-2x = 2,5 ; -2x = ln 2,5 ; x = -ln2,5 / 2 ~
-0,458.
3. En déduire le
tableau des variations de la fonction f sur R.
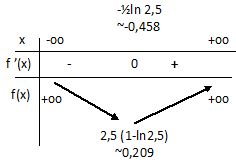
4. a. Déterminer à
partir du tableau des variations le nombre de solutions de l’équation f
(x) = 2.
Cette équation admet deux solutions : une solution sur chaque
intervalle où f(x) est monotone.
b. Donner une valeur arrondie à 10−2 près de chaque solution.
e-2x+5x = 2.
Graphiquement on trouve -0,95 et 0,28.
A l'aide d'une calculatrice, on trouve : e+1,9 +5(-0,95)
~1,94.
e+1,92
+5(-0,96) ~2,02. On retient -0,96.
e-0,56
+5 x 0,28 ~1,97.
e-058
+5 x 0,29 ~2,001. On retient +0,29.
Partie C. : Calcul
d’aire
On admet :
• que la courbe C de la partie A est la représentation de la fonction f
définie dans la partie B;
• que la courbe C se situe « au-dessus » de la droite tangente T sur R.
L’objectif de cette partie est de déterminer par un calcul l’aire A
comprise entre la courbe C, la droite T et les droites verticales
d’équations x = 0 et x = 1,5.
1. Hachurer sur le
dessin l’aire A que l’on veut déterminer.
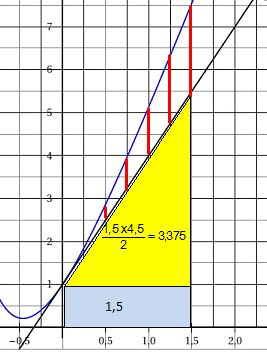
2. a. Déterminer
une primitive de la fonction g définie sur R par :
pour tout réel x, g (x)= e−2x+2x −1.
G(x) = -½e−2x+x2
−x.
La
courbe C est au dessus de T, d'équation y = 3x+1. f(x) -(3x+1) =e−2x
+5x-3x-1 = e−2x
+2x-1 = g(x).
c.
En déduire la valeur exacte puis l’arrondi à 10−2 de A.
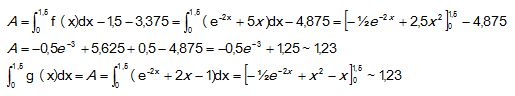
|
|
|
Métropole septembre 2016.
Dans
une entreprise de fabrication de pièces métalliques, un ouvrier doit
manipuler des plaques chaudes pendant une dizaine de secondes. À la
sortie du four, les plaques sont à une température de 300 °C et
disposées dans une pièce dont la température ambiante est maintenue à
26 °C par un système de ventilation. La commission de sécurité prescrit
qu’avec les gants actuels, l’ouvrier doit attendre 10 minutes pour
manipuler les plaques à leur sortie du four. Afin de réduire ce délai
d’attente, le directeur s’interroge sur l’achat de nouveaux gants dont
les caractéristiques techniques établies par la commission de sécurité
sont les suivantes :
Sans couture. Très doux et confortables. Température maximale
d’utilisation : 240 °C.
1. Dans
cette question, on ne demande pas de justification.
a. Quelle est, à la
sortie du four, la température des plaques ? 300°C.
b. Comment varie, à
la sortie du four, la température des plaques au cours du temps ?
La température des plaques diminue au cours du temps de 300°C à 26°C.
c. Vers quelle
valeur la température des plaques devrait-elle se stabiliser ?
A la température de la pièce où elles sont entreposées,soit 26°C.
2.
La température d’une plaque depuis sa sortie du four, est modélisée en
fonction du temps t , exprimé en minutes, par une fonction g .On admet
que cette fonction g est définie sur l’intervalle [0 ; +oo[ par g (t )
= 274eat+26 où a est un nombre réel.
a. Calculer g (0).
Ce résultat est-il conforme aux données ?
g(0) = 274 e0 +26 = 300°C, en accord avec les données.
b. D’après la
question 1, quel doit être le signe du nombre réel a ?
a doit être négatif, car la temprature des plaques diminue.
c.
On sait que 3 minutes après sa sortie du four la température de la
plaque, arrondie à l’unité, est de 262 °C. Montrer que la valeur
approchée à 10−2 près du coefficient a est −0,05.
g
(3 ) = 274e3a+26 =262 ; 274e3a
=262-26 =236 ;
e3a
=236 / 274 = 0,8613 ; 3a = ln 0,8613 ; a = -0,0497 ~-0,05.
3.
Dans cette question on considère que, pour tout nombre réel t de
l’intervalle [0;+oo[ :
g (t )= 274e−0,05t+26.
a.
Avec les gants actuellement utilisés, à quelle température l’ouvrier
pourra t-il manipuler les plaques après leur sortie du four, en
respectant les caractéristiques techniques de la commission de sécurité
?
g(10) = 274e−0,05*10+26
=274e−0,5+26
= 192°C.
b.
Si le directeur décidait d’équiper les ouvriers avec les nouveaux
gants, quel délai d’attente minimal serait requis avant que les
ouvriers puissent manipuler les plaques ?
g(t) = 274 e−0,05t+26
= 240 ; 274
e−0,05t
= 240-26 = 214 .
e−0,05t
=214 / 274 = 0,781 : -0,05t = ln 0,781 = -0,2472 ; t = 0,2472 / 0,05
=4,94~5 minutes.
c.
En déduire le gain de temps, en pourcentage, dû à l’utilisation de ces
nouveaux gants.
(10-4,94) / 10 *100 =50,6 ~ 51%.
|
|
|
|
Métropole 06 / 2016.
Quand l’oreille humaine est soumise à une intensité acoustique,
exprimée en watts par mètre carré (W/m2), le niveau sonore
du bruit responsable de cette intensité acoustique est exprimé en
décibels (dB).
1. D’après le
tableau, lorsque l’intensité acoustique estmultipliée par 10, quelle
semble être l’augmentation du niveau sonore ?
Quand l'intensité acoustique est multipliée par 10, le niveau sonore
augmente de 10 dB.
Concert et discothèque I = 10-1 W m-2 ; niveau
sonore 110 dB.
Baladeur à puissance maximum : I = 10-2 W m-2 ;
niveau sonore 100 dB.
2. La relation
liant l’intensité acoustique x où x appartient à l’intervalle [10−12;106]
et le niveau sonore est donnée par :
f(x) = 4,34 ln x +120.
a. Vérifier la
conjecture émise à la question 1.
Quand x est multiplié par 10 : ln10 ~ 2,30 ; 4,34 ln 10 ~10,1 dB.
b. Quel serait le
niveau sonore de deux motos ?
Pour une moto x = 10-5 W m-2. ; pour deux motos
identiques 2x = 2 10-5 W m-2.
f(2x) = 4,34 ln (2 10-5) +120 ~73,0 dB.
3.
Pour éviter tout risque sur la santé, le port d’un casque de protection
acoustique est donc conseillé au delà de 85 dB. Déterminer l’intensité
acoustique à partir de laquelle le port d’un tel casque est conseillé.
85 = 4,34 ln x + 120 ; 4,34 ln x = 85-120 = -35 ; lnx = -35 /4,34 =
-8,0645 ; x = 3,15 10-4 W
m-2.
Antilles Guyanne 2016.
Sur
le graphique ci-dessous, C est la courbe représentative, dans le repère
orthonormé (O, i, j) d’une fonction f définie sur R.
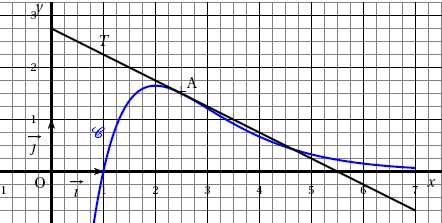
Partie A - Étude graphique.
La droite T est tangente à C au point A(2,5 ; 1,5) et d’ordonnée à
l’origine 2,75.
L’axe des abscisses est asymptote horizontale à C au voisinage de +∞.
Déterminer graphiquement et indiquer sur votre copie :
1. f (1) = 0.
2. f ′(2,5) = pente
de la tangente à la courbe en A.
f '(2,5) = -(2,75 -0 / 5,5 = -0,5.
3. Une équation de
la tangente T.
y = -0,5 x + 2,75.
4. La limite de
f(x) quand x tend vers l'infini.
L'axe des abscisses est asymptote à la courbe. La limite de f(x) est
égale à zéro quand x tend vers l'infini.
Partie B -Modélisation.
On admet qu’il existe deux réels a et b tels que : pour tout réel x, f
(x) = (ax +b)exp(−x+2,5).
1. Calculer f ′(x)
en fonction de a et b.
On pose u = ax+b et v = exp(−x+2,5).
u' = a et v' = -exp(−x+2,5).
Dérivée d'un produit : f '(x) = u'v +v'u = a exp(−x+2,5)-(ax+b)
exp(−x+2,5).
f '(x) = (-ax+a-b)exp(−x+2,5).
2. Exprimer en
fonction des réels a et b les nombres suivants :
f (1) = (a+b)exp(1,5) ; f ′(2,5) = (-1,5 a -b)e0 =-1,5 a -
b.
3. Déduire des
questions précédentes un système d’équations vérifiées par a et b.
(a+b)exp(1,5) = 0 soit a +b = 0.
-0,5 = -1,5 a - b.
4. Résoudre ce
système et en déduire l’expression de f (x) en fonction de x.
a = -b ; -0,5 = 0,5 b ; b = -1
et a = 1 et f(x) = (x-1)exp(−x+2,5).
|
|
Partie C - Étude algébrique.
On admet que pour tout réel x, f (x) = (x −1)exp(−x+2,5).
1. Déterminer la
limite de f en −∞.
Le
terme en exponentielle tend vers l'infini et que x-1 tend vers
moins l'infini quand x tend vers moins l'infini.. f(x) tend donc
vers moins l'infini.
2. a. Montrer que
pour tout réel x,
b. Déterminer la
limite de f en +∞.
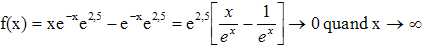
3. a. Calculer f
′(x) pour tout réel x.
On pose u = x-1 et v = exp(−x+2,5)
; u' = 1 et v' = -exp(−x+2,5).
Dérivée d'un produit : u'v +v'u = exp(−x+2,5)-(x-1)exp(−x+2,5).
f '(x) = (2-x)exp(−x+2,5).
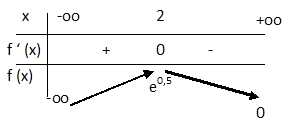
b.
Étudier le signe de f ′ et en déduire le tableau des variations de la
fonction f en faisant figurer les limites trouvées précédemment.
exp(−x+2,5)
est toujours positif ;le signe de f ' (x) est celui de 2-x ; positif
pour x <2 ; nul pour x =2 et négatif pour x >2.
PartieD - Application.
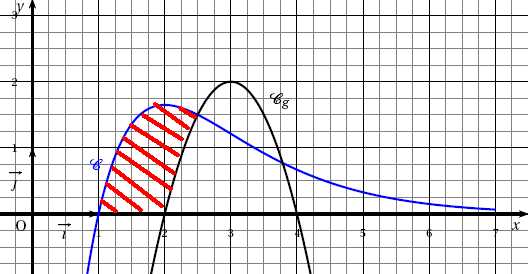
On
souhaite déterminer l’aire S en unité d’aire de la surface d’une des
faces principales du boîtier plastique de l’appareil auditif schématisé.
Une modélisation mathématique a permis de représenter cette surface.
Dans le plan muni du repère orthonormé (O, i, j ), cette surface
correspond à la partie du plan limitée par :
• l’axe des abscisses ;
• les droites d’équations x = 1 et x = 2,5 ;
• la courbe représentative C de la fonction f étudiée précédemment ;
• la courbe représentative Cg de la fonction g définie par
: pour tout réel x, g (x) = −2x2+12x −16.
1. Hachurer la
surface décrite précédemment.
Pour déterminer l’aire S de cette surface, on décompose le calcul en
deux parties.
2. Calculer la
valeur exacte de l’intégrale suivante :
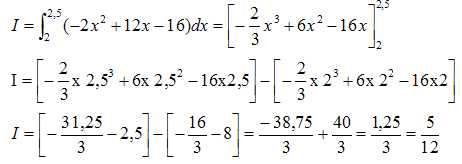
3. On souhaite
calculer la valeur exacte de l’intégrale suivante :
a. Vérifier qu’une
primitive F de la fonction f sur R est la fonction définie par, pour
tout réel x, F(x) = −x exp(−x+2,5).
F '(x)=- exp(−x+2,5)+ x exp(−x+2,5)= (x-1)exp (−x+2,5).
b. En déduire la
valeur exacte de l’intégrale J.
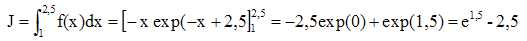
4. a. Déterminer la
valeur exacte de l’aire S en unité d’aire.
b. En déduire la
valeur arrondie à 10−2 de l’aire S en unité d’aire.
e1,5 -30 / 12 -5 / 12 =e1,5 -35 / 12 ~1,565 ~1,57.
Nlle Calédonie.
Le bassin d’une piscine municipale a une capacité de 600 000 litres
d’eau. Afin de respecter les normes d’hygiène et de sécurité, 30 000
litres d’eau de la piscine sont renouvelés chaque heure et le taux de
chlore maximum autorisé est de 0,25 mg/L.
Un soir après la fermeture de la piscine, alors que le taux de chlore
est indétectable, 1 kg de chlore est déversé par erreur dans le bassin
à 20 h. Le directeur de la piscine souhaiterait savoir quand il pourra
ouvrir à nouveau la piscine au public.
On modélise la concentration massique du chlore présent dans la piscine
par une fonction f . Lorsque t désigne le temps écoulé depuis
l’accident, exprimé en heures, f (t ) représente la concentration
massique du chlore présent dans la piscine en milligrammes par litre.
On admet que la fonction f est solution de l’équation différentielle
(E) :
y′ +0,05y = 0 où y désigne une fonction de la variable t .
1. a. Résoudre
l’équation différentielle (E).
b. Que vaut f (0) ? En déduire une expression de f (t ) sur [0 ; +∞[.
f(t) = A e-0,05t avec A une constante définie à partir des
conditions initiales.
1 kg = 106 mg ; f(0) = 106 / 600 000 = 10 /6 = 5
/ 3 ~1,67 mg / L.
f(t) = 5 / 3 e-0,05t .
2. On admet que f
est définie sur [0 ; +∞[ par f (t ) =5 / 3 e-0,05t .
À quel moment la piscine pourra-t-elle ouvrir de nouveau au public ?
5 / 3 e-0,05t <
0,25 ; e-0,05t <
0,25 x3 / 5 ; e-0,05t < 0,15.
-0,05t <
ln(0,15) ; -0,05t <
-1,897 ; t > 1,897
/ 0,05 ; t >37,94.
La piscine peut ouvrir au bout de 38 heures.
|
|