Mathématiques,
bac
STi2D et STL Polynésie 2017 .
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice 1. 4 points
Cet
exercice est un questionnaire à choix multiples. Pour chacune des
questions suivantes, une seule des quatre réponses proposées est
exacte. Aucune justification n’est demandée. Une bonne réponse rapporte
un point. Une mauvaise réponse, plusieurs réponses ou l’absence de
réponse à une question ne rapportent ni n’enlèvent de point.
Pour répondre, vous recopierez sur votre copie le numéro de la question
et indiquerez la seule réponse choisie.
1. La forme
exponentielle du nombre complexe z est :
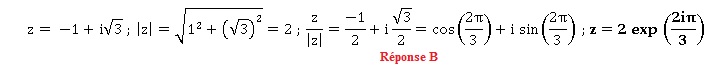 2.
2. L'intégrale
suivante est égale à :
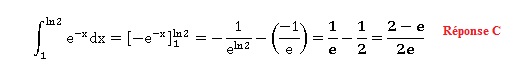 3.
3. Si f est la
fonction définie sur ]0 ; +∞[ par f (x) = 2x −lnx, alors la limite de f
quand x tend vers 0 + est :
a. +oo ; b. 0 ; c.
2 ; d. ln2.
Quand x tend vers 0 +, 2x tend vers zéro et lnx tend vers -oo.
f(x) tend vers plus l'infini.
4. Soit G la
fonction définie pour tout réel x strictement positif par
G(x) : x lnx −x +2
G est une primitive de la fonction g définie sur ]0, +∞[ par :
a. g(x) = x lnx-1 ; b.
g(x) = ln x +2x ; c. g(x)=1-0,,5x2 +2x ; d. g(x) = ln x
Dériver G(x). On pose u =x et v = lnx ; u'=1 et v' =1/x.
u'v +v'u = lnx+1.
G'(x) = lnx+1-1 = ln x.
Exercice 2.
(4 points)
En 2016,
l’Organisation Mondiale de la Santé (OMS) affirme que 5,1 millions de
personnes en France souffraient de
diabète, soit 8% de la population.
Chaque personne dispose d’un
dossier médical régulièrement actualisé.
Partie
A.
Dans le cadre de la semaine
nationale de prévention du diabète qui s’est tenue en 2016, une
campagne de sensibilisation de
cette maladie a été menée.
Sur 85 dossiers médicaux
prélevés au hasard, on a compté 3 cas de diabète.
1.
Quelle est la fréquence de cas de diabète dans l’échantillon prélevé ?
f = 3 / 85 ~0,0353.
2. Déterminer l’intervalle de
fluctuation avec un niveau de confiance de 95% de la fréquence de cas de
diabète sur cet échantillon de
85 dossiers.
1,96 [ p(1-p) / n]½=1,96 [0,08
(1-0,08) / 85]½=1,96 x0,0200 =0,0576.
Intervalle de fluctuation : [0,08 -0,0576 ; 0,08 +0,0576] soit [0,022 ; 0,138].¸
3.
L’échantillon est-il représentatif de la population française ?
Justifier.
0,035 appartient à cet intervalle. L’échantillon est représentatif de la
population française.
|
....
...
|
Partie B.
Dans le corps humain, la régulation du taux de glycémie est assurée
grâce à un équilibre permanent entre différentes substances
principalement hormonales.
Le tableau suivant présente trois états de la glycémie :
Hypoglycémie à jeun : inférieur à 0,70 g/l
Glycémie normale à jeun : entre 0,70 g/l et 1,10 g/l
Hyperglycémie à jeun : supérieur à 1,10 g/l
On note N la variable aléatoire qui, à chaque dossier médical prélevé
au hasard dans la population, associe le taux de glycémie à jeun en g/l
de la personne. On suppose que N suit la loi normale de moyenne 0,9 et
d’écart type 0,1.
Dans le cadre de cet exercice, on considère qu’une personne souffre de
diabète si cette personne ne présente pas une glycémie normale à jeun.
1. Déterminer la
probabilité pour que le dossier prélevé soit celui d’une personne en
hypoglycémie.
P(N <0,7) =0,02275 ~0,023.
2. Déterminer la
probabilité pour que le dossier prélevé soit celui d’une personne en
hyperglycémie.
P(N >1,10) =1-P(N <1,10) = 1-0,9772 =0,0227 ~0,023.
3. Déterminer la
probabilité que le dossier prélevé soit celui d’une personne souffrant
de diabète.
P(N <0,7) +P(N >1,10) =0,02275 +0,0227 ~0,045.
Exercice
3. 6 points.
Les trois
parties de cet exercice peuvent être traitées demanière indépendante.
Une note demusique est émise en pinçant la corde d’une guitare
électrique.
La puissance du son émis, initialement de 100 watts, diminue avec le
temps t ,mesuré en seconde.
On modélise par f (t ) la puissance du son émis, exprimée en watt, t
secondes après le pincement de la
corde.
Partie A.
On considère l’équation différentielle (E) suivante où y est une
fonction de la variable t définie et dérivable sur l’intervalle [0 ,
+∞[ et où y′ est la fonction dérivée de y :
(E) : 25y′ +3y = 0
1. Résoudre
l’équation différentielle 25y′ +3y = 0.3 /25 y=0.
y' +3 /25 y =0 ; y' +0,12 y=0.
Solution générale : y = A exp(-0,12 t)
avec A une constante.
2. Déterminer la
fonction f solution de l’équation différentielle (E) qui vérifie la
condition initiale f (0) =100.
f(0) =100 = A e0 ; A = 100 ;
f(t) = 100 exp(-0,12 t).
3. Quelle est la
puissance du son deux secondes après le pincement de la corde ?
Arrondir au watt près.
f(2) = 100 exp(-2 x0,12) = 100 e-0,24 ~78,7 W.
|
|
|
Pour la suite de l’exercice, on admet que la fonction f est définie sur
l’intervalle [0 ;+∞[ par :
f (t )= 100exp(−0,12t).
Partie B.
On s’intéresse à l’instant à partir duquel la puissance du son émis
après le pincement de la corde sera inférieure à 80 watts.
On considère l’algorithme suivant :
Initialisation
a prend la valeur 0
b prend la valeur 5
Traitement
Tant que |b −a| > 0,2
m prend la valeur (a+b) /
2
Si f (m) > 80
a prend la valeur m
Sinon
b prend la valeur m
Fin si
Fin tant que
Sortie
Afficher a, b.
1. À l’aide de
l’algorithme ci-dessus, compléter le tableau.
a
|
0
|
0
|
1,25
|
1,25
|
1,5625
|
1,71875
|
b
|
5
|
2,5
|
2,5
|
1,875
|
1,875
|
1,875
|
b-a
|
5
|
2,5
|
1,25
|
0,625
|
0,3125
|
0,15625
|
|b-a|
>0,2
|
vrai
|
vrai
|
vrai
|
vrai
|
vrai
|
faux
|
m
|
2,5
|
1,25
|
1,875
|
1,5625
|
1,71875
|
1,71875
|
f(m)
|
74,1
|
86
|
79,85
|
82,9
|
81,36
|
81,36
|
f(m)>80
|
faux
|
vrai
|
faux
|
vrai
|
vrai
|
vrai
|
2. Quelles sont les
valeurs affichées en sortie de cet algorithme ?
a = 1,71875 ; b = 1,875.
3. Dans le contexte
de cet exercice, que représentent ces valeurs ?
a et b représentent l'intervalle [a ; b] pendant lequel la puissance
sonore devient inférieure à 80 W.
Partie C.
1. Résoudre par le
calcul l’équation f (t ) = 80, on donnera la valeur exacte et la valeur
approchée à 10−3
près. Interpréter ce résultat.
100exp(−0,12t) <
80 ; exp(-0,12t) < 0,8 ; -0,12 t < ln 0,8 ;
t > -ln(0,8) / 0,12
; t >1,860 s.
2. Calculer et interpréter la
limite de f lorsque t tend vers +∞.
-0,12 t est négatif. .Le terme en exponentielle tend vers zéro.
Par suite f(t) tend vers
zéro.
Au bout d'un temps très long, la puissance sonore est nulle
|
|
|
|
Exercice 4. 6 points
Dans un parc
régional, on étudie une espèce de renards. Cette population était de 1
240 renards à la fin de l’année 2016.
On modélise par un le nombre de renards dans le parc
régional à la fin de l’année 2016+ n. On a donc
u0 = 1240.
On estime à 15% par an la baisse du nombre un.
On suppose que cette évolution restera identique pour les années à
venir.
Dans cet exercice, les résultats seront arrondis à l’unité.
Partie A.
1. Montrer qu’à la
fin de l’année 2017 ,la population de renards sera de 1 054.
u1 = u0(1-0,15)=1240 x(1-0,15) = 1240 x 0,85 =
1054.
2. a. Donner la
valeur de u1 puis calculer u2.
u1 =1054 ; u2 = u1 x0,85 = 1054 x0,85
= 895,9 ~896.
b. Exprimer un+1
en fonction de un.
un+1 =
0,85 un.
c. En déduire la
nature de la suite (un) et préciser ses éléments
caractéristiques.
Il s'agit d'une suite géométrique de premier terme 1240 et de raison
0,85.
3. Déterminer une
estimation du nombre de renards présents dans le parc régional à la fin
de l’année 2020.
n = 4 ; u4 = 1240 x0,854 ~647.
4. Déterminer la
limite de la suite (un). Comment interpréter ce résultat ?
q = 0,85 ; 0 < q <1, donc qn tend vers zéro si n tend
vers l'infini.
La suite (un) tend vers zéro. Les renards vont disparaître
du parc.
5. Des
scientifiques considèrent que l’espèce des renards présents dans le
parc sera en situation d’extinction.
à partir du moment où le nombre de renards deviendra strictement
inférieur à 100.
À partir de quelle année l’espèce de renards présents dans le parc
sera-t-elle en situation d’extinction?
1240 x0,85n < 100 ; 0,85n < 100 / 1240 ;
La fonction logarithme étant strictement croissante, n ln 0,85
< ln (100 / 1240).
n < (ln100 -ln1240) / ln0,85 ; n > 15,49
2016 +16 =2032.
A partir de 2032,
l'espèce sera en voie d'extinction.
Partie B.
Afin de préserver l’espèce, on décide d’introduire à chaque année 30
renards à partir de la fin de l’année 2017.
On note vn le nombre de renards présents dans le parc à la
fin de l’année 2016+n.
On estime à 15% par an la baisse du nombre vn.
On a v0 = 1240.
1. Calculer v1.
v1 =0,85 v0+30 =0,85 x1240 +30 =1084.
2. Dans cette
question, toute trace de réponse cohérente sera prise en compte.
On admet que pour tout entier naturel n on a vn =
200+1040×0,85n .
Que pensez-vous de l’affirmation suivante : « Le nombre de renards va
diminuer et se stabiliser vers 200 ».
Quand n tend vers l'infini, le terme 1040 x0,85n tend vers
zéro. Donc vn tend vers 200.
L'affirmation est exacte.
|
|