Mathématiques,
bac
STi2D et STL Antilles 2017 .
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice 1. 4 points
Cet
exercice est un questionnaire à choix multiples. Pour chacune des
questions suivantes, une seule des quatre réponses proposées est
exacte. Aucune justification n’est demandée. Une bonne réponse rapporte
un point. Une mauvaise réponse, plusieurs réponses ou l’absence de
réponse à une question ne rapportent ni n’enlèvent de point.
Pour répondre, vous recopierez sur votre copie le numéro de la question
et indiquerez la seule réponse choisie.
Dans cet exercice, i désigne le nombre complexe de module 1 et
d’argument ½ p.
1. La suite (u n)
est définie par u 0 = −3 et pour tout entier naturel n, u n+1
=7 / 5u n.
La limite quand n tend vers +∞de (u n) est :
a. 0 ; b. −∞ ; c. +∞ ; d. −3.
La suite est géométrique de raison 7 / 5 et dse premier terme u 0
= -3.
u n = -3 x(7 / 5) n.
7 / 5)n
tend vers l'infini quand n tend vers l'infini.
un
= -3 x(7 / 5)n tend vers moins l'infini quand n tend vers
l'infini.
2. On considère la
suite géométrique (v n) définie par son premier terme v 0
=0,25
et sa raison q =1,5
La valeur exacte du terme v 10 est égale à :
a. 14,4 ; b. 7,3×10 −4 ; c.
59049 / 4096 ; d. 15 / 4.
v10
= 0,25 x(1, 5)10 =0,25 x 59049 / 1024 =59049 / 4096.
3. On considère le
nombre complexe z =3 ½-5i. Le nombre complexe suivant est
égal à :
4. Le nombre a est
un réel strictement positif. Le nombre complexe z = a +ia 3 ½
admet pour forme
exponentielle :

|
....
...
|
Exercice 2.
(7 points)
En
1648, Blaise Pascal a demandé à son beau-frère Florin Périer de mesurer
la hauteur de mercure dans deux baromètres, l’un situé à
Clermont-Ferrand et l’autre en haut de la montagne la plus proche, le
Puy-de-Dôme.
Florin Périer a constaté que la hauteur de mercure dans le baromètre
situé en haut du Puy-de-Dôme
était inférieure à la hauteur de mercure dans le baromètre situé plus
bas, à Clermont-Ferrand.
Cette expérience a permis de montrer que la pression atmosphérique
diminue lorsque l’altitude augmente. Dans cet exercice, la pression
atmosphérique est exprimée en hectopascal (hPa).
On rappelle que la pression atmosphérique vaut 1013,25 hPa au niveau de
la mer.
Partie A : Une
règle simplifiée
Pour évaluer la pression atmosphérique, les alpinistes utilisent la
règle simplifiée suivante : « la pression atmosphérique diminue de 0,11
hectopascal quand l’altitude augmente de 1 mètre ».
1. Recopier et
compléter le tableau suivant en utilisant cette règle :
Altitude
(m)
|
0
|
800
|
1500
|
2000
|
Pression
atmosphérique ( hPa)
|
1013,25 |
1013,25
-800 x0,11
=925,25
|
1013.25-1500
x0,11
=848,25
|
1013.25-2000
x0,11
=793,25
|
2. Pour tout entier naturel n, on
note un la pression atmosphérique en hPa à l’altitude de n
mètres
calculée avec la règle simplifiée.
Ainsi u0 = 1013,25.
a. Calculer u1 et u2.
u1 =u0-0,11 =1013,14 ; u2 = u0-2
x 0,11 =u1-0,11 =1013,03.
b. Justifier que la
suite (un) n’est pas géométrique.
un = u0 - 0,11 n diffère de u0 x qn.
(un) n'est pas une suite géométrique.
c. On admet que
pour tout entier naturel n, un = u0 −0,11n.
En déduire l’altitude, exprimée en mètre, à partir de laquelle la
pression atmosphérique est
inférieure à 950 hPa.
1013,25 -0,11 n < 950 ; 1013,25-950 < 0,11 n ; n >575.
Partie B : La
formule barométrique
On considère l’équation différentielle (E) :
y′ +0,12y = 0
où y est une fonction de la variable réelle x, définie et dérivable sur
R et y′ est la fonction dérivée de y. Pour de faibles valeurs de
l’altitude, les scientifiques ont démontré que la fonction f qui, à
l’altitude x en kilomètre, associe la pression atmosphérique en
hectopascal est la solution de l’équation différentielle (E) qui
vérifie f (0) = 1013,25.
1. a. Déterminer
les solutions de l’équation différentielle (E).
Solution générale de (E) : y = A exp(-0,12 x) avec A une constante.
f(0) = A exp(0) ; A = 1013,25 ; f(x) = 1013,25
exp(-0,12 x).
b. Démontrer que la
solution f de l’équation différentielle (E) qui vérifie la condition
initiale
f (0) = 1013,25 est la fonction définie sur [0 ; +∞[ par : f (x) =
1013,25 exp(−0,12x).
f '(x) = -0,12 x1013,25 exp(-0,12x) = -121,59exp(-0,12x).
Repport dans (E) :
-121,59 exp(-0,12x) + 0,12 x1013,25 exp(-0,12x) =0
-121,59 exp(-0,12x) + 121,59 exp(-0,12x)
=0 est vérifié quelque soit x.
2. En utilisant la fonction f :
a. Calculer une
valeur approchée à 0,01 près de la pression atmosphérique à 150 mètres
d’altitude.
f(0,150) = 1013,25 exp(-0,12 x0,150) =995,17
hPa.
b. Calculer
l’altitude, arrondie au mètre, correspondant à une pression
atmosphérique de 900 hPa.
900 = 1013.25 exp(-0,12x) ; ln(900 / 1013.25) = -0,12x ;
-0,11852 = -0,12 x ; x = 0,988 km = 988
m.
3. On pose vn
= f (n), pour tout entier naturel n. Justifier qu’avec ce modèle, la
suite (vn) est géométrique.
v0 = 1013.25 ; v1 = 1013,25 e-0,12 =v0
e-0,12 ; v2 = 1013,25 e-0,24
=v1 e-0,12 ;
vn = v0 e-0,12 n .
Partie C : La
formule du nivellement barométrique
La formule de la partie B ne tient pas compte des changements de
température et ne peut donc être
utilisée que pour de faibles altitudes.
Pour des altitudes plus élevées, on utilise la fonction p qui à
l’altitude x en kilomètre associe la pression atmosphérique en hPa :
p(x)= 1013,25 [ 1-6,5x / 288,15]5,255.
1. Calculer la
pression atmosphérique (en hPa, arrondie à l’unité) au sommet de
l’Everest dont l’altitude est 8 848 mètres.
p(8,848)=
1013,25 [ 1-6,5 * 8,848 / 288,15]5,255~315 hPa.
2.
Recopier et compléter l’algorithme suivant en utilisant la fonction p,
de façon à ce qu’il affiche
en sortie l’altitude (estimée à 100 mètres près) à partir de laquelle
la pression atmosphérique est
inférieure à 400 hPa.
Variables
A un nombre réel
P un nombre réel
Début
A prend la valeur 0
P prend la valeur 1 013,25
Tant que P >400 faire
A prend la valeur A+0,1
P prend la valeur 1013,25 [ 1-6,5*A / 288,15]5,255.
Fin tant que
Afficher A
Fin
|
|
|
Exercice
3. 4 points.
Dans cet exercice, ln désigne la fonction logarithme népérien et
l’unité de longueur est le mètre (m).
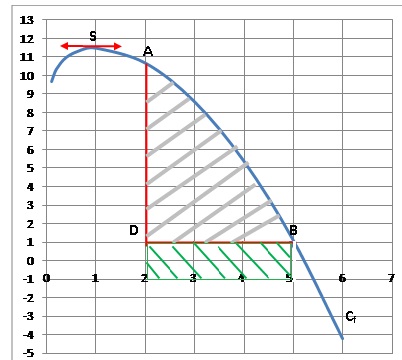
Un ingénieur prépare un plan pour fabriquer la voile d’un petit bateau.
La voile est représentée en gris dans le repère orthonormé ci-dessous
où une unité représente un mètre.
Cf est la représentation graphique de la fonction f définie
sur [0,1 ; +∞[ par :
f (x) = 12+ax2 +ln(x).
où a est un nombre réel qui sera déterminé dans la partie A.
S est le point de Cf d’abscisse 1.
A est le point de Cf d’abscisse 2.
B est le point de Cf d’abscisse 5.
D est le point d’intersection de la droite d’équation x = 2 et de la
droite parallèle à l’axe des abscisses passant par B.
La voile est représentée par le domaine délimité par le segment [AD],
le segment [DB] et la courbe Cf .
Partie A
La fonction f ′ désigne la fonction dérivée de f .
1. On suppose que
la tangente à la courbe Cf au point S est horizontale. Que
vaut f ′(1) ?
f '(1) = 0,
tangente horizontale en S.
2. Calculer f ′(x)
pour tout réel x de [0,1 ; +∞[.
f '(x) = 2ax +1 /x.
3. a. Exprimer f
′(1) en fonction de a.
f '(1) = 2a +1.
b. Démontrer que a
= −0,5 .
f '(1) = 0 = 2a +1 soit a = -0,5.
Partie B
1. Montrer que la
fonction F définie sur [0,1 ; +∞[ par F(x) = 11x −x3 /6
+xln(x)
est une primitive de f sur [0,1 ; +∞[.
Dérivée de x ln(x) : on pose u = x et v = ln(x) ; u' =1 ; v' = 1/x.
u'v+v'u = ln(x) +1.
F '(x) = 11 -3x2 /6 +ln(x) +1 = 12 -0,5 x2 +ln(x)
= f(x).
2. a. Calculer la
valeur exacte, exprimée en unité d’aire, de l’aire du domaine limité
par la courbe
Cf , l’axe des abscisses et les droites d’équation x = 2 et
x = 5.
A =F(5)-F(2)=11 x5 -53/6 +5ln(5)-[11 x2 -23/6
+2ln(2)].
A = 55-22-125 / 6 +8 /6 +ln(55) -ln(22).
A = 33-19,5 +ln(55 / 22) = 13,5 +ln(55 / 22).
b. Vérifier qu’une valeur approchée
de cette aire, arrondie au dixième, est 20,2 m2.
A ~13,5 +6,66 ~20,2 m2.
3. Cette voile doit être légère tout
en étant suffisamment résistante. Elle est fabriquée dans un tissu
ayant une masse de 260 grammes par mètre carré. La voile pèsera-t-elle
moins de 5 kg ? Justifier la réponse.
f(5)
= 12 -0,5 x52 +ln(5) = ln(5)-0,5.
Aire du rectangle hachurée en vert. 3(ln(5)-0,5) = 3 ln(5) -1,5 ~3,3 m2.
Aire de la voile : 20,2 -3,3 =16,9 m2.
Masse de la voile : 16,9 x0,260 ~4,4 kg.
La
voile pèse moins de 5 kg
|
|
|
|
Exercice 4. 5 points
Dans cet exercice,
les résultats demandés seront arrondis à 10−3, sauf
indication contraire.
Partie A.
Pour dépister les maladies de la glande thyroïde chez un patient, on
mesure le taux d’une hormone appelée TSH.
Un médecin étudie les dossiers médicaux des patients de son hôpital.
On désigne par X la variable aléatoire qui, à un dossier pris au hasard
dans cet hôpital, associe le taux de TSH du patient correspondant.
On suppose que X suit la loi normale de moyenne μ= 2,2 et d’écart type s = 0,9.
1. Déterminer p(X
< 3).
P(X <3) = 0,813.
2. Déterminer la
probabilité qu’un dossier médical pris au hasard dans cet hôpital
présente un taux de TSH compris entre 1,5 et 3,5.
P(X <1,5) = 0,21835 : P(X <3,5) =0,92569.
P (1,5 < X <3,5) = 0,92569 -0,21835
~0,707.
3. Pour les
dossiers médicaux dont le taux de TSH est supérieur à 4, les médecins
prescrivent des examens complémentaires au patient.
Déterminer la probabilité qu’un dossier médical pris au hasard dans cet
hôpital corresponde à un patient qui nécessite des examens
complémentaires.
P(X >4) = 1 -P(X <4) = 1- 0,97725~0,023.
Partie B.
En 2012, l’Agence Nationale de Sécurité du Médicament (ANSM) s’est
inquiétée de la forte augmentation des ventes du médicament qui traite
l’hypothyroïdie. Pour obtenir un état des lieux de l’utilisation de ce
médicament en France, l’ANSM a effectué un sondage sur 530 877
personnes.
Dans cet échantillon, 21 771 personnes ont déclaré qu’elles utilisaient
ce médicament.
1. Quelle est la
fréquence des utilisateurs du médicament dans l’échantillon étudié ?
f = 21 771 / 530 877 ~0,041.
2. Déterminer un
intervalle de confiance avec un niveau de confiance de 95% de la
proportion d’utilisateurs de ce médicament dans la population française.
1,96 [f (1-f) / n )½ = 1,96 [0,041 x(1-0,041) / 530 877]½=1,96
x2,72 10-4 ~5,3 10-4.
Intervalle de confiance [ 0,041 -5,3 10-4 ; 0,041 +5,3 10-4)
soit [0,0405 ; 0,415].
Partie C.
En médecine, on utilise de l’iode radioactif pour traiter certaines
maladies de la glande thyroïde.
La durée de vie exprimée en heure d’un atome d’iode radioactif est
modélisée par une variable aléatoire D qui suit la loi exponentielle de
paramètre l =
0,0036, exprimé en h−1.
1. Calculer la
durée de vie moyenne en heure de l’atome d’iode radioactif. On
arrondira le résultat à l’unité.
1 / 0,0036 ~278 h.
2. Déterminer P(24
<D < 48). Interpréter le résultat.
P(D<48) -P(D <24) = 1 - exp(-0,0036 x48) -(1-exp(-0,0036 x24)) =
exp(-0,08648)-exp(-0,1728)=0,9172-0,8413 =0,0759 ~0,076.
3. On appelle
demi-vie d’un élément radioactif le temps T, exprimé en heure,
nécessaire pour que la moitié des atomes radioactifs d’une substance se
soit désintégrée. Autrement dit, ce réel T est tel que P(D < T ) =0,5
a. Démontrer que T
=ln(2) / l.
P(D < T ) =0,5 =1-exp(-lT)
; exp(-lT) =0,5 ;
ln(0,5) = -ln(2) = -lT
; T =ln(2) / l.
b. En déduire la
demi-vie de l’iode radioactif. Donner le résultat en jour.
T = ln (2) / 0,0036 = 192,5 h ou 192,5 /24 ~ 8 jours.
|
|