Mathématiques, bac STi2D et STL Métropole 2017 . En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Exercice 1. La climatisation d’un véhicule automobile est un système qui a une double fonction, refroidir ou réchauffer l’habitacle. Ce système fonctionne grâce à une certaine masse de gaz réfrigérant stocké dans un réservoir. On suppose que, par défaut d’étanchéité, le système perd naturellement 0,1 gramme de ce gaz chaque jour. Un automobiliste possède un véhicule pour lequel la masse de gaz dans le réservoir est initialement de 660 grammes. Partie A. Le constructeur préconise de recharger le réservoir lorsque la masse de gaz est inférieure à 440 grammes. Au bout de combien de jours le constructeur préconise-t-il à l’automobiliste de recharger ce réservoir ? Perte totale de gaz avant recharge :660-440 =220 g Nombre de jours avant recharge : 220 / 0,1 = 2200 jours. ou bien : suite arithmétique de premier terme 660 et de raison r = -0,1. un = 660 -0,1 n. 660-0,1 n < 440 ; n > (660-440) / 0,1. Partie B. Lors d’une visite d’entretien, le garagiste signale à l’automobiliste que le système de climatisation de son véhicule présente une baisse significative de masse de gaz : en plus de la perte naturelle de 0,1 gramme, le système perd 1% de sa masse de gaz chaque jour. Le garagiste recharge alors complètement le réservoir. Pour tout entier naturel n, on note un la masse de gaz dans le réservoir au bout de n jours après cette visite. On a donc u0 = 660 et on admet que pour tout entier naturel n, on a : un+1 = 0,99un -0,1. 1. Calculer u1 et u2. u1 =0,99 u0-0,1 =0,99 x660-0,1 =653,3. u2 =0,99 u1-0,1 =0,99 x653,3-0,1 =646,667. 2. Voici un algorithme qui, lorsque l’on saisit un nombre N non nul de jours écoulés, calcule et affiche la masse de gaz restant dans le système. Variables N : un nombre entier naturel k : un nombre entier naturel u : un nombre réel Entrée Saisir N Initialisation u prend la valeur 660 Traitement Pour k allant de 1 à N u prend la valeur 0,99 u-0,1 Fin pour Sortie Afficher u a. Recopier et compléter la partie relative au traitement de cet algorithme. b. Quelle masse de gaz restera-t-il au bout de 20 jours ? Arrondir au gramme près. 3. Soit la suite (vn) définie pour tout entier naturel n par vn = un +10. a. Calculer v0. v0 = u0 +10 = 660 +10 = 670. b. On admet que (vn) est une suite géométrique de raison 0,99. Pour tout entier naturel n, exprimer vn en fonction de n. vn =v0x0,99n. c. En déduire que, pour tout entier naturel n, on a : un = 670x0,99n -10. un =vn -10 =v0x0,99n-10=670 x0,99n-10. d. À l’aide de cette expression, vérifier le résultat obtenu à la question 2.b. u20 = 670 x0,9920-10 ~538. 4. On rappelle que le constructeur préconise de recharger le réservoir au plus tard lorsque la masse de gaz est inférieure à 440 g. Le coût d’une recharge est de 80 euros. Le garagiste propose de réparer le système pour 400 euros. Pourquoi est-il plus économique pour cet automobiliste de réparer le système? Justifier la réponse. 670 x0,99n-10 < 440 ; 0,99n < 450 /670 ; 0,99n < 0,6716 ; n ln(0,99) < ln (0,6716) ; n > 39,6 . Tous les 40 jours il faut faire une recharge. Coût au bout d'un an : 80 x9 = 720 €. Il vaut mieux réparer. .... ... Exercice 2. La fonte GS (graphite sphéroïdal) possède des caractéristiques mécaniques élevées et proches de celles des aciers. Une entreprise fabrique des pièces de fonte GS qui sont utilisées dans l’industrie automobile. Ces pièces sont coulées dans desmoules de sable et ont une température de 1400 °C à la sortie du four. Elles sont entreposées dans un local dont la température ambiante est maintenue à une température de 30 °C. Ces pièces peuvent être démoulées dès lors que leur température est inférieure à 650 °C. La température en degrés Celsius d’une pièce de fonte est une fonction du temps t , exprimé en heures, depuis sa sortie du four. On admet que cette fonction f , définie et dérivable sur l’intervalle [ 0 ; +oo[  , est une solution sur cet intervalle de l’équation différentielle y'+0,065y =1,95. 1. a. Résoudre sur [ 0 ; +oo[  l’équation différentielle y'+0,065y =1,95  (E).. Solution de l'équation y' +0,065y =0 : y = A exp(-0,065 t) avec A une constante. Solution particulière de (E) : y = 1,95 / 0,065 = 30. Solution générale de (E)  : y = A exp(-0,065 t ) +30. b. Donner f (0) et vérifier que la fonction f est définie sur l’intervalle [ 0 ; +oo[ par f (t ) =1370 exp(-0,065 t ) +30. f(0) = 1370 ; A e0 +30 = 1400 ; A = 1400-30 = 1370. f (t ) =1370 exp(-0,065 t ) +30. 2. a. Étudier mathématiquement le sens de variation de la fonction f sur l’intervalle [ 0 ; +oo[ f '(t) = -1370 x0,065 exp(-0,065t) = -89,05 exp'-0,065t). le terme en exponentielle étant positif, la dériv"e f '(t) est négative et la fonction f(t) est strictement décroissante.. b. Pourquoi ce résultat était-il prévisible ? La température de la pièce diminue de 1400 °C à 30°C. 3. La pièce de fonte peut-elle être démoulée après avoir été entreposée 5 heures dans le local ? f(5) = 1370 exp(-0,065 x5) +30 ~1020°C, valeur supérieure à 650°C ; la pièce ne peut pas être démoulée. 4. a. Déterminer au bout de combien de temps au minimum la pièce pourra être démoulée. Arrondir le résultat à laminute près. 650 = 1370 exp(-0,065 t) +30 ; 620 / 1370 = exp(-0,065t) ; 0,4525 = exp(-0,065 t) ; ln(0,4525) = -0,065t ; t = 12,2 h soit 12 h 12 min. b. Pour éviter la fragilisation de la fonte, il est préférable de ne pas démouler la pièce avant que sa température ait atteint 325 °C. Dans ce cas, faudra-t-il attendre exactement deux fois plus de temps que pour un démoulage à 650 °C ? Justifier la réponse. Non, durée de refroidissement et température ne sont pas proportionnelles. 325 = 1370 exp(-0,065 t) +30 ; 295 / 1370 = exp(-0,065t) ; 0,2153 = exp(-0,065 t) ; ln(0,2153) = -0,065t ; t = 23,6 h soit 23 h 36 min. Exercice 3. Un chef cuisinier décide d’ajouter un « menu terroir » à la carte de son restaurant. S’appuyant sur sa longue expérience, le restaurateur pense qu’environ 30% des clients choisiront ce menu. Ceci le conduit à faire l’hypothèse que la probabilité qu’un client, pris au hasard, commande le «menu terroir » est p = 0, 3. Partie A. Afin de tester la validité de son hypothèse, le restaurateur choisit au hasard 100 clients et observe que 26 d’entre eux ont commandé un « menu terroir ». Après discussion avec son comptable, le restaurateur décide d’accepter l’hypothèse que p = 0, 3. À l’aide d’un intervalle de fluctuation asymptotique à 95%, justifier cette décision. n = 100 > 30 ; np = 100 x0,3 = 30 > 5 ; n(1-p) =100 x0,7 = 70 > 5. Lex conditions sont réunies pour définir un intervalle de fluctuation asymptotique à 95 %. 1 / n½ = 1 /100½ = 0,1. Par suite [0,26-0,1 ; 0,26 +0,1] soit [0,16 ; 0,36]. La valeur 0,3 appartient à cet intervalle. La décision du restaurateur est justifiée. Partie B. Une agence de voyage a réservé toutes les tables du restaurant pour la semaine à venir. Le restaurateur sait ainsi que 1000 clients viendront déjeuner chacun une fois durant la semaine. Le nombre de « menus terroir » qui seront alors commandés est une variable aléatoire X. On considère que la probabilité qu’un des clients commande un «menu terroir » est p= 0, 3. 1. On admet que la variable aléatoire X suit une loi binomiale. a. Donner ses paramètres. n = 1000  ; p =0,3. b. Déterminer la probabilité que le nombre de « menus terroir » commandés soit inférieur ou égal à 315. P(X < 315)~0,857. 2. On décide d’approcher la loi binomiale précédente par la loi normale d’espérance  µ= 300 et d’écart type s= 14,49. Justifier ces valeurs . µ = n p = 1000 x0,3 = 300 ; s = (np(1-p))½ = (1000 x0,3 x0,7)½=14,49. Dans la suite de l’exercice, on utilisera cette approximation par la loi normale. Les résultats seront arrondis à 10-2 près. 3. a. Estimer P(285 < X < 315). P(X < 315)~0,857 ; P(X < 285)~0,1585. P(285 < X < 315)= 0,857-0,1585 ~0,6985 ~0,70. b. Estimer P(X > 350) et interpréter le résultat obtenu. P(X > 350) = 1 -P(X < 350 ) =1-0,9997 ~ 3 10-4 ~0. Le restaurateur est certain qu'il n'y aura pas plus de 350 menus terroir. Exercice 4. Pour chacune des propositions suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie. Toute trace de recherche, même incomplète ou non fructueuse, sera prise en compte dans l’évaluation. Une réponse non justifiée ne rapporte aucun point. 1. Proposition 1 : Le nombre complexe z de module 4 x3½  et dont un argument est 2p/3 apour forme algébrique z = -2 x3½ +6i. Vrai. z =4 x3½  [cos (2p/3)+i sin(2p/3)] =4 x3½  [-0,5)+i 3½ /2] = -2 x3½ +6i. 2. Le plan est muni d’un repère orthonormé direct . Les points A, B et C ont pour affixes respectives zA = 2exp(ip/2) , zB = -1 +i 3½ et zC=zA x zB. Proposition 2 : Le point C appartient au cercle de centre O et de rayon 4. Vrai. 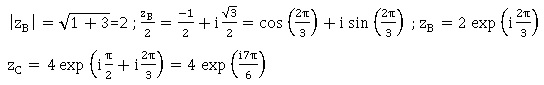Le module de zC est égal à 4. C est sur le cercle de centre O et de rayon 4. 3. On a tracé ci-dessous dans un repère orthonormé ( la courbe représentative C de la fonction f définie sur l’intervalle [0 ; 2}par f (x) =-0,5x+1. On considère un point M de coordonnées (x,-0,5x+1) sur la courbe C , ainsi que les points H(x,0) et K(0,-0,5x+1) Proposition 3 : L’aire, en unités d’aire, du rectangle OHMK est maximale lorsque M a pour abscisse 1. Vrai. 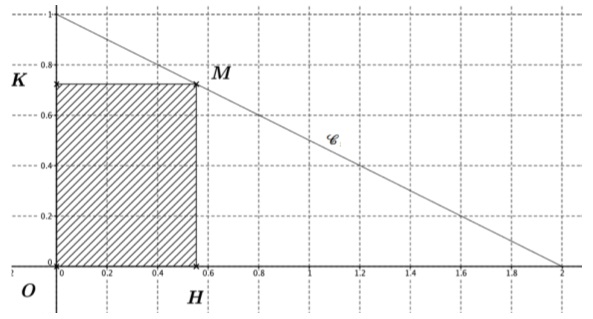OH =x ; OK = -0,5x+1 ; Aire du rectangle =A = OH *Ok = x(-0,5 x+1) =-0,5x2 +x. Le maximum est atteint pour x = -b / (2a) =-1 /(-2*0,5) = 1. 4. On peut modéliser le temps d’attente d’un client, en minutes, à la caisse d’un supermarché par une variable aléatoire T qui suit une loi exponentielle de paramètre l. Des études statistiques montrent que la probabilité qu’un client attende plus de 7 minutes à cette caisse est 0,417. On rappelle que pour tout réel t positif, P(T > t ) = exp(-lt). Proposition 4 : Le temps moyen d’attente à cette caisse de supermarché est 9 minutes. Faux. 0,417 = exp(-7l) ; ln(0,417) = -7 l ; l ~0,125 ;  1 / l = 8. L'espérance vaut 8 minutes. .

menu