Mathématiques,
probabilités
Bac Sti2d et Stl 2016.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie juin 2016.
Deux
amis ont monté un atelier associatif pour réparer des vélos. Le but de
cette association est que chaque adhérent puisse venir réparer son vélo
dans cet atelier avec l’aide d’un spécialiste. Le matériel et les
outils sont fournis.
Partie A : les
roulements à billes.
Nos deux amis commandent régulièrement des lots de 60 roulements à
billes pour les vélos. Ils ont constaté que, lors de leur dernière
livraison, sur le lot des 60 roulements à billes, 3 étaient défectueux.
Ils s’inquiètent donc de la fiabilité du fabricant.
Le contrat précise que seulement 4% des pièces sont défectueuses.
1. Calculer la
fréquence des pièces défectueuses dans le dernier lot.
3 / 60 = 0,05.
On considère que les pièces constituant ce lot forment un échantillon
prélevé de façon aléatoire dans un stock dans lequel 4% des pièces sont
défectueuses.
2. Déterminer
l’intervalle de fluctuation asymptotique à 95% de la fréquence des
roulements à billes non conformes dans un échantillon de 60 roulements.
Les valeurs approchées seront arrondies à 10−2.
n = 60 ; p = 0,04 ; q = 1-p = 0,96.
[p q /n]½ = [0,04 x 0,96 / 60]½ =0,0253 ; 1,96
*0,0253 = 0,0496~0,050.
Intervalle de confiance [ 0,04-0,05 ; 0,04 +0,05] soit : [-0,01 ; 0,09].
3. Nos amis ont-ils
raison de s’inquiéter ? Justifier votre réponse
0,05 appartient à cet intervalle, nos amis n'ont pas à s'inquiéter.
Partie B : les
billes
Nos amis se demandent s’ils ne devraient pas plutôt commander des
billes pour réparer les roulements évoqués dans la partie A.
Ils commandent une grande quantité de billes de 6 mm de diamètre.
Malheureusement, certaines présentent un défaut de diamètre. Ils
s’aperçoivent qu’ils ne peuvent utiliser que les billes mesurant entre
5,9 mm et 6,1 mm.
Sur la note du fabricant est indiqué que la variable aléatoire D qui, à
chaque bille, lui associe son diamètre, suit la loi normale d’espérance
µ = 6 mm et d’écart-type s
= 0,05 mm.
Question : Calculer la probabilité que D appartienne à l'intervalle
[5,9 ; 6,1 ]. Le résultat sera arrondi à 10−2.
(D-µ)
/ s suit la loi normale centrée
réduite :
(5-9 -6) / 0,05 = -2 ; (6,1
-6) / 0,05 = +2 ; les tables donnent t = 0,9772.
2 *0,9772 -1 = 0,9544 ~0,95.
Partie C : les chaînes de vélo
Un tableau est mis à disposition pour permettre aux utilisateurs de
savoir quand ils doivent changer leur chaîne de vélo. Par exemple, pour
une personne utilisant son vélo en ville (vitesse moyenne 16 km.h−1)
environ 2 heures par jour, la durée de vie moyenne de la chaîne est de
625 jours.
On admet que la durée de vie en jour, d’une chaîne de vélo pour un tel
utilisateur est une variable aléatoire X qui suit une loi exponentielle
de paramètre l.
On rappelle que la probabilité que X soit inférieure ou égale à t
(exprimé en jour) vaut :
P(X <= t ) = 1−exp(−l¸t
).
1. Démontrer que l = 0,0016.
L'espérance mathématique de cette loi est égale à E(X )= 1 / l = 1 / 625 ; l = 0,0016 jour-1.
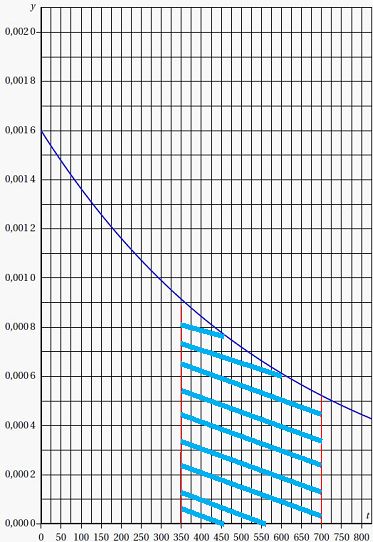
2. Le graphique
représente la fonction de densité de la loi exponentielle de paramètre l= 0,0016 jour-1..
a. Représenter sur
ce graphique la probabilité que X soit comprise entre 350 jours et 700
jours.
Cette probabilité est représentée par l'aire hachurée.
b. Calculer la
probabilité que X soit comprise entre 350 jours et 700 jours. Arrondir
le résultat à 10−3.
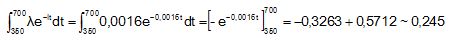
3. Calculer la
probabilité que X soit de moins de 550 jours. Arrondir à 10−3.
1- exp ( -0,0016 x 550) = 1-exp(-0,88) = 1-0,4148 = 0,585.
4. Déterminer la
valeur de x pour que P(X < x) = 0,8. Le résultat sera arrondi à
l’unité. Interpréter ce résultat en le restituant dans le contexte.
1- exp(-0,0016 x) = 0,8 ;
exp(-0,0016 x) =0,2 ; -0,0016 x = ln 0,2 ; x = ln 0,2 /
0,0016 ~1006 jours.
La probabilité qu'une chaîne dure 1006 jours est égale à 0,8.
|
|
|
Métropole septembre 2016.
Une
usine métallurgique fabrique des boîtes de conserve pour des
entreprises spécialisées dans le conditionnement industriel de légumes.
La probabilité qu’une boîte prélevée au hasard soit non conforme est
0,04.
Un lot de 200 boîtes choisies au hasard est livré à une
entreprise spécialisée dans le conditionnement des légumes. Le nombre
de boîtes fabriquées par cette usine métallurgique est assez important
pour pouvoir assimiler un tel prélèvement à un tirage avec remise de
200 boîtes.
PARTIE A.
La variable aléatoire X désigne le nombre de boîtes non conformes dans
un tel lot.
1. Justifier que la
variable aléatoire X suit une loi binomiale dont on précisera les
paramètres.
Les
prélevements sont indépendants et leur nombre est fixé à n = 200. La
probabilité qu'une boîte soit non conforme est constante p = 0,04. La
probabilité qu'une boîte soit conforme est q = 0,96.
X
suit la loi binomiale de paramètre n = 200 et p = 0,04.
2.
Déterminer la probabilité qu’un tel lot contienne exactement quatre
boîtes non conformes.
p(X=4)=C4200 q196 p4 =200*199*198*197
/ (2*3*4) *0,96196 *0,044=0,276.
p(X=4)=5,55
10-2 ~ 0,055.
PARTIE B.
On décide d’approcher la loi binomiale suivie par X par la loi normale
d’espérance µ= 8 et d’écart type s = 2,77.
1. Justifier le choix de ces
paramètres.
µ
~np = 200*0,04 = 8 ; s ~(npq)½= (
200*0,4*0,96)½=2,77.
2.
À l’aide de la loi normale ainsi définie :
a. calculer
P(6<= X <= 10) et interpréter le résultat trouvé ;
(6-µ) / s = (6-8)
/ 2,77 = -0,722 ; (10-µ)
/ s = (10-8) /
2,77 = +0,722 ;
Loi normale centrée réduite : P(-0,722 <= (X-µ) / s <= 0,722).
Les tables donnent P(0,722) ~ 0,765
2P(t)-1 =2*0,765
-1 ~0,53.
La probabilité de trouver dans ce lot, un nombre de boîtes non
conformes
compris entre 6 et 10,
bornes comprises, est égal à 53 %.
b.
Déterminer une approximation de la probabilité qu’il y ait au maximum 4
boîtes non conformes.
Il faut calculer
P(X< =4).
(4-µ)
/ s = (4-8) /
2,77 = -1,444 ; les tables donnent P(1,444) ~0,9256.
Puis 1 -0,9256 ~0,074.
Partie C.
Dans le lot livré de 200
boîtes, on compte 11 boîtes non conformes. Le fabricant des boîtes est
averti. Doit-il s’inquiéter ?
(pq / n)½ =(0,04 *0,96 /200)½
= 0,01386.
Intervalle de fluctuation avec un seuil de confiance de 95 % :
[0,04 -0,01386 *1,96 ; 0,04 +0,01386 *1,96] soit [0,013 ;
0,067 ].
11 / 200 = 0,055, cette valeur appartient à l'intervalle de fluctuation.
Le fabriquant ne doit pas s'inquiété, aves un risque de 5 %.
|
|
|
|
Métropole 06 / 2016.
Un
pont levant enjambant un canal peu fréquenté est constitué d’un tablier
qui, une fois relevé, permet le passage de bateaux de différentes
tailles.
Hauteur du tablier en position haute : 7mètres. Longueur du tablier :
30 mètres
Temps de montée du tablier : 2 minutes
Temps en position haute du tablier (hors incident) : 8 minutes. Temps
de descente du tablier : 2 minutes.
Partie A - Sur la
route
Un
automobiliste se présente devant le pont. Le tablier du pont est en
position haute. On s’intéresse ici au temps d’attente D, exprimé en
minutes, de l’automobiliste avant qu’il puisse franchir le canal, pont
baissé (hors incident).
1. Combien de temps
l’automobiliste attend-il au minimum ? au maximum ?
2 minutes si le
pont comence à descendre ;
10 minutes si le pont
est en fin de montée.
2.
On admet que le temps d’attente, en minutes, de l’automobiliste pour
franchir le pont est une variable aléatoire D qui suit la loi uniforme
sur l’intervalle [2 ; 10]. Déterminer l’espérance E(D) de la variable
aléatoire D et interpréter le résultat dans le contexte.
E(D) = (2+10) / 2 = 6.
En moyenne un automobiliste attend 6 minutes.
3. Calculer la
probabilité que le temps d’attente de l’automobiliste ne dépasse pas 5
minutes.
p(2 <=D <=5) =(5-2) / 6 = 0,5.
Partie B - Sur
l’eau
Dans cette partie les résultats demandés seront arrondis à 10−2
près.
Lorsqu’un
bateau est passé, le tablier du pont revient en position basse. Le
temps, exprimé en heures, avant que le bateau suivant se présente
devant le pont est une variable aléatoire T qui suit la loi
exponentielle de paramètre l =
0,05. Ce temps est appelé temps de latence.
1. Déterminer
l’espérance E(T ) de la variable aléatoire T et interpréter le résultat
dans le contexte.
E(T) =1 / l = 1
/0,05 = 20.
En moyenne, un bateau se présente toutes les 20 heures.
2. On considère la
fonction f définie sur [0 ; +∞[ par f (x) = 0,05exp(−0,05x) .
a. Montrer que la
fonction F définie sur [0 ; +∞[ par F(x) = −exp(−0,05x ) est une
primitive de f.
Dériver F(x) : F '(x) = 0,05 exp(−0,05x ) = f(x).
b. Démontrer
que P(T <=t ) = 1−exp(−0,05t ).
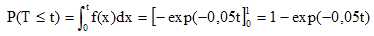
3. a. Calculer la
probabilité que le temps de latence soit inférieur à une demi journée,
soit 12 heures.
p(T <=12) = 1-exp(-0,05 *12) =1-0,549 ~ 0,45.
b. Calculer la
probabilité que le temps de latence soit supérieur à un jour.
p(T <=24) = 1-exp(-0,05 *24) ~0,70 ; p(T > 24 ) = 1-0,70 = 0,30.
c. Calculer
P(12<=T <=24).
1-0,45 -0,30 = 0,25.
|
|
Antilles Guyanne 2016.
Un
manufacturier de pneumatiques produit des pneus d’avions en grande
quantité. Il s’engage à livrer des produits spécifiques aux avionneurs
de masse maximum garantie de 124 kg. Ces pneus doivent supporter une
charge nominale de 10 tonnes, des vitesses pouvant aller jusqu’à 420
km.h−1 et des températures instables allant de −40 °C (en
altitude) à 250 °C (au moment du décollage).
Partie A.
On
note M la variable aléatoire qui, à chaque pneu prélevé au hasard dans
la production, associe sa masse en kilogramme. On admet que la variable
aléatoire M suit la loi normale de moyenne μ = 121,37 et d’écart type s = 0,42.
1. Déterminer la
probabilité qu’un pneu prélevé au hasard ait une masse en kg comprise
entre 120,95 et 121,79.
(120,95 -121,37) / 0,42 = -1 ; (121,79
-121,37) / 0,42 =+1 ;
Loi normale centrée réduite ( -1 <= (M-µ) / s <= 1) ; les tables
donnent pour t = 1, P(1)
= 0,841 3 ;
2P(1) -1=2*0,8413 -1 = 0,6826
~0,683.
2.
Déterminer la probabilité qu’un pneu prélevé au hasard ait une masse en
kg supérieure à 122,63.
(122,63 -121,37) / 0,42
= 3 ; P(3) =0,998 65 ; 1-0,998 65 ~0,00135.
Partie B.
Un pneu trop lourd entraîne une augmentation de la consommation du
kérosène.
Lorsque
la masse d’un pneu reçu par une compagnie aérienne dépasse 121,9 kg
cela entraîne des pénalités financières pour le manufacturier.
Sur
la chaîne de fabrication, on prélève de façon aléatoire un échantillon
de 36 pneus et on constate que 2 d’entre eux ont une masse qui dépasse
121,9 kg.
1. Quelle est la
fréquence des pneus dans l’échantillon prélevé dont la masse dépasse
121,9 kg ?
p = 2 /18 =1/9 ~0,111 ; q = 1-p
= 8 /9 ; n = 36.
2.
Déterminer l’intervalle de confiance avec un niveau de confiance de 95%
de la proportion de pneus dont la masse dépasse 121,9 kg dans la
production.
(p q / n)½ =[ 8 /(81+36)]½=0,05238 ; 1,96
*0,05238 = 0,10266;
Intervalle de confiance [0,111 -0,1026 ; 0,11 +0,1026 ] soit [0,0085 ; 0,214 ].
3. Donner une
interprétation du résultat précédent.
La proportion de pneus ayant une masse supérieure à 121,9 kg est
comprise entre 0,85 % et 21,4 % avec un risque d'erreur de 5 %.
Nlle Calédonie.
Les deux parties de cet exercice peuvent être traitées de manière
indépendante. Dans l’ensemble de l’exercice, les résultats seront
arrondis à 10−3 près.
Une usine fabrique des batteries au lithium-ion pour des vélos
électriques. Le cahier des charges indique qu’une batterie mesure 15 cm
de large.
Lors de la fabrication, on modélise la largeur des batteries par une
variable aléatoire X qui suit une loi normale de moyenne μ = 15 et
d’écart-type s =
0,02. L’objectif de cet exercice est d’analyser la qualité de la
production dans cette usine.
Partie A.
Une batterie est jugée conforme lorsque sa largeur, exprimée en
centimètres, appartient à l’intervalle [14,95 ; 15,05].
1. Calculer la
probabilité qu’une batterie prélevée au hasard dans la production soit
non conforme.
(15,05 -15) / 0,02 = 2,5.
Loi normale centrée réduite
( -2,5 <= (X-µ) / s
<= 2,5) ; les tables donnent pour t = 2,5, P(2,5) = 0,9938 ;
Probabilité qu'une batterie soit non conforme : 1-0,9938 = 0,0062 ~0,006.
L’usine vend ses batteries au lithium-ion par lots
de 2 000 aux fabricants de vélos électriques.
En moyenne, chaque lot de 2 000 batteries en contient 24 non conformes.
On note p la probabilité qu’une batterie soit non conforme. On prélève
au hasard 2 000 batteries dans la production. La production est assez
importante pour que l’on puisse assimiler ce
prélèvement à un tirage aléatoire avec remise.
On modélise le nombre de batteries non conformes dans un lot de 2 000
par une variable aléatoire Y.
2. Quelle loi suit
la variable aléatoire Y ? Préciser ses paramètres.
Les
prélevements sont indépendants et leur nombre est fixé à n = 2000. La
probabilité qu'une batterie soit non conforme est constante p = 24
/2000 =0,012. La
probabilité qu'une bbatterie soit conforme est q = 1-0,012=0,988.
X
suit la loi binomiale de paramètre n
= 2000 et p = 0,012.
3. Calculer la
probabilité qu’il y ait au moins 30 batteries non conformes dans un lot
de 2 000 batteries.
La calculatrice donne P(Y >30)
=0,095.
Partie B.
Dans le cadre d’un fonctionnement correct des machines de la chaîne de
production, on admet que la proportion p de batteries non conformes est
1,2%.
Le responsable de l’usine affirme qu’il ne vend pas de lot de 2 000
batteries qui en contienne plus de 40 non conformes. Quelle est la
fiabilité de cette affirmation ? Justifier.
Recherche d'un intervalle de fluctuation au seuil de 95 % : 1,96
(p(1-p)/n)½ =1,96(0,012 x0,988 /2000)½=0,00477.
[0,012-0,00477 ; 0,012 +0,00477 ) soit : [0,0072 ; 0,0168 ]
le nombre de batteries non conforme dans ce lot est compris entre
0,0072 x2000 ~ 15 et 0,0168 x2000 ~34.
Cette affirmation est vraie.
|
|