Mathématiques, étude de fonction, suite géomètrique Bac St2S 2016. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Métropole 2016.  On étudie la durée d’allaitement maternel d’un groupe de 1 000 nourrissons nés le même jour. À la fin de chaque semaine après la naissance, on compte le nombre de nourrissons encore allaités maternellement. Partie A. Le tableau ci-dessous, extrait d’une feuille de calcul, donne semaine après semaine le nombre de nourrissons encore allaités maternellement. A B C D E F G H I 1 Nombre de semaines depuis la naissance 1 2 3 4 5 6 7 8 2 Nombre de nourrissons encore allaités maternellement 595 572 551 534 505 485 472 453 3 Pourcentage d'évolution -3,9 %   1. Déterminer le pourcentage d’évolution, entre la deuxième et la troisième semaine, du nombre de nourrissons encore allaités maternellement. Le résultat sera arrondi à 0,1%. (572-551) / 572 *100 = -3,67 %. 2. Les cellules C3 à I3 sont au format pourcentage arrondi à 0,1%. Proposer une formule à saisir dans la cellule C3 qui, recopiée vers la droite, permet de calculer le pourcentage d’évolution entre deux semaines consécutives du nombre de nourrissons allaités maternellement. =(C$2-B$2) / B$2. Partie B. Soit f la fonction définie sur l’intervalle [0 ; 100] par : f (x) = 620×0,96x . 1. On admettra que la fonction f a les mêmes variations que la fonction g définie sur l’intervalle [0 ; 100] par g (x) = 0,96x . Déterminer, en justifiant, le sens de variation de la fonction f sur l’intervalle [0 ; 100]. Si 0 < a < 1, alors la fonction qui à x associe ax est une fonction strictement décroissante sur R. Dans ce cas a = 0,96, nombre strictement inférieur à 1, en conséquence la fonction x |-->0,96x est une fonction strictement décroissante sur [0 ; 100]. Par suite la fonction f est strictement décroissante sur l’intervalle [0 ; 100]. 2. Compléter le tableau de valeurs, correspondant à la fonction f. Les résultats seront arrondis à l’unité. x 0 5 10 20 30 40 60 80 100 f(x) 620 506 412 274 182 121 54 24 10 3. Tracer l’allure de la représentation graphique de la fonction f dans le repère fourni. 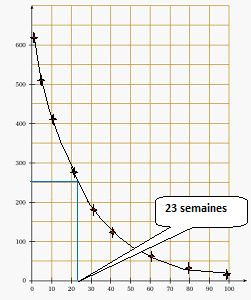4. a. Résoudre graphiquement l’inéquation f (x) <= 250. Tracer les pointillés nécessaires et donner une valeur approchée du résultat avec la précision permise par le graphique. b. Retrouver le résultat précédent par le calcul. 250 <= 620 *0,96x ; 250 / 620 <= 0,96x ; log(250 / 620) <= x log 0,96 ; -0,394 <= -0,0177 x  ; x > 22,25. c. On modélise, à l’aide de la fonction f , le nombre de nourrissons allaités maternellement. Ainsi, f (x) donne une estimation du nombre de nourrissons encore allaités maternellement, x semaines après leur naissance. Selon ce modèle, estimer le nombre de semaines à partir duquel moins d’un quart des nourrissons seront encore allaités maternellement. 23 semaines. Partie C Dans cette partie, on modélise, à l’aide d’une suite géométrique, le nombre de nourrissons allaités maternellement. On suppose que ce nombre diminue de 4% chaque semaine. Pour tout entier n strictement positif, on note Un une estimation du nombre de nourrissons encore allaités maternellement n semaines après leur naissance. Ainsi U1 = 595. 1. Justifier que la raison de la suite géométrique (Un) est 0,96. U2 = U1 (1-0,04) = 0,96 U1 ; U3 = U2 (1-0,04) = 0,96 U2 = 0,962 u1. On passe d'un terme au suivant en multipliant ce terme par 0,96. Il s'agit d'une suite géométrique de raison 0,96 et de premier terme U1= 595. 2. Pour tout entier n >1, exprimer Un en fonction de n. U3 = U2 (1-0,04) = 0,96 U2 = 0,962 u1. un = 0,96n-1 u1 = 595 un-1. 3. Selon ce modèle, à combien peut-on estimer le nombre de nourrissons encore allaités maternellement 24 semaines (soit environ 6 mois) après leur naissance ? u24 =  595 x 0,9623 = 233. Métropole septembre 2016. Le service d’urgence d’un hôpital reçoit un patient infecté par une bactérie très virulente. Des prélèvements sanguins sont régulièrement effectués afin de suivre l’évolution du nombre de bactéries en fonction du temps. Tous les prélèvements réalisés ont le même volume. Dans le premier prélèvement effectué au moment de l’admission du patient, on dénombre 19 000 bactéries. La situation évoluant très rapidement, on administre au bout de trois heures un puissant antibiotique dont l’effet est immédiat. Dans toute cette étude, on note t, le temps ( en heures) écoulé depuis le premier prélèvement. Soit f  la fonction définie pour tout réel t ∈ [0 ; 12], par f (t )= −t3 +9t2 +21t +190. On considère que cette fonction permet de modéliser, en fonction du temps. le nombre de bactéries (en centaines) présentes dans le prélèvement effectué sur le patient à l’instant t . Ainsi f (3) est le nombre de centaines de bactéries présentes dans le prélèvement sanguin effectué au bout de 3 heures après l’admission du patient à l’hôpital. Partie A : Étude de la fonction f 1. Calculer f (0), f (7), f (12). f(0) = 190 ; f(7) = -73 +9 x72+21 x 7 +190 = -343+441+147+190 =435. f(12) =-123 +9 x122+21 x 12 +190 = -1728+1296+252+190 =10. 2. Soit f ′ la fonction dérivée de la fonction f . Calculer f ′(t ) pour tout réel t ∈ [0 ; 12]. f '(t) = -3t2+ 18 t +21. On admettra pour la suite de cette partie que la dérivée peut s’écrire sous la forme : f ′(t )= −3(t +1)(t −7). 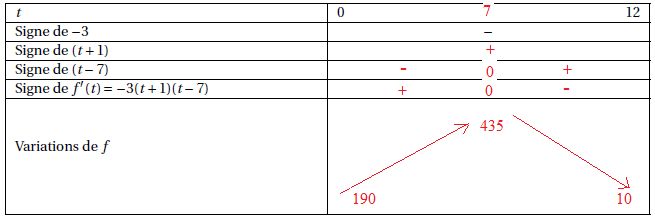3. Compléter le tableau qui donne le signe de la dérivée f ′ et les variations de f. 4. Calculer f ′(10). f '(10) = -3 (10+1)(10-7) =-3 x 11 x 3 = -99. Partie B : Application On donne une représentation graphique de la fonction f . 1. Par lecture graphique, déterminer le nombre de bactéries dans le prélèvement effectué trois heures après l’admission du patient à l’hôpital. 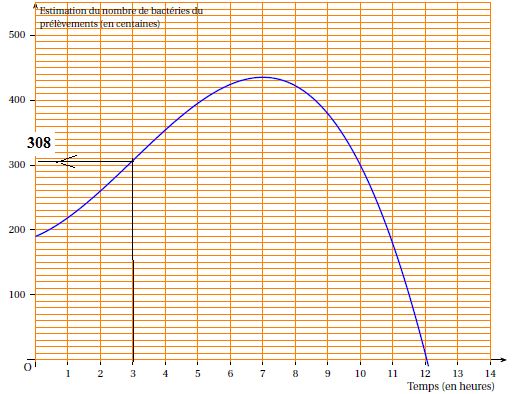30 800 bactéries sont présentes 3 heures plus tard. 2. Comment se traduit graphiquement l’effet de l’antibiotique, à partir dumoment où il est administré ? L'antibiotique est peu efficace durant les quatre premières heures qui suivent son administration et le nombre de bactéries croît. Au bout de 7 heures, l'antibiotique est suffisamment efficace pour détruire les bactéries et les empécher de se multiplier. 3. La situation d’un patient est critique, lorsque le nombre de bactéries dans un prélèvement atteint 50 000.Le patient étudié risque-t-il d’être en situation critique au cours des 12 premières heures suivant sonadmission à l’hôpital ? Justifier la réponse. Non, le nombre maximum de bactéries est égale  à 43 500, valeur inférieure à 50 000. 4. La vitesse de croissance du nombre de bactéries à l’instant t est donnée par f ′(t ) qui est le nombre dérivé de la fonction f en t . Déterminer la vitesse de croissance du nombre de bactéries pour t = 10 heures, c’est-à-dire 10 heures après la prise en charge du patient par l’hôpital. f '(10) = -99. Antilles-Guyanes 2016. Le laboratoire pharmaceutique Clamex fabrique et commercialise un vaccin contre la rougeole. Sa capacité de production, sur une semaine, lui permet de réaliser entre 0 et 17 litres de ce produit. On note x le volume de production exprimé en litres. On note B(x) le bénéfice hebdomadaire (en euros) réalisé par le laboratoire pour la vente du volume x de vaccin. 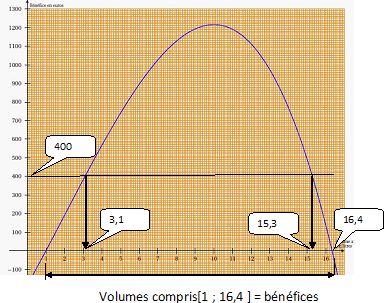La courbe représentative de la fonction B définie sur l’intervalle [0 ; 17] est donnée en annexe 1. Partie A : Lecture graphique Les résultats aux questions posées dans cette partie seront donnés en s’aidant du graphique. 1. Déterminer les volumes hebdomadaires vendus pour lesquels le bénéfice hebdomadaire est égal à 400 euros. 2. Pour quels volumes hebdomadaires vendus, le laboratoire Clamex est-il bénéficiaire ? Partie B : étude du bénéfice hebdomadaire On admet que la courbe donnée est la représentation graphique de la fonction B définie sur l’intervalle [0 ; 17] par B(x) = −x3 +6x2 +180x −184. On note B′ la fonction dérivée de la fonction B. 1. a. Déterminer B′(x) pour tout réel x appartenant à l’intervalle [0 ; 17]. B'(x) = -3x2 +12x+180. b. Montrer que B′(x) = (−3x +30)(x +6) pour tout réel x appartenant à l’intervalle [0 ; 17]. Développer : B'(x) =-3x2-18x+30x+180 = -3x2 +12 x +180. Autre méthode : Discriminant D' = 62-180 x(-3) =576. Racine carrée du discriminant : 24 Solutions :( -6 +24 ) (-3)= -6 et (-6 -24) / (-3) = 10. B'(x) = -3 (x+6) (x-10). c. Étudier le signe de B′(x) sur l’intervalle [0 ; 17]. d. En déduire le tableau de variations de la fonction B sur l’intervalle [0 ; 17]. On fera apparaître les valeurs de la fonction B aux bornes de l’intervalle. B(10) = -1000+600+1800-184 =1216. B(17) = -173 +6 x172 +180 x17 -184 = -4913+1734 +3060 -184 =-303. 2. Déterminer le volume hebdomadaire vendu pour obtenir un bénéfice maximal et calculer la valeur de ce bénéfice, en euros. Le bénéfice est maximum ( 1216 € ) pour une production hebdomadaire égale à 10 L. Polynésie 2016. Lors de sa première année de vie, un enfant a deux types d’anticorps dans le sang : les anticorps transmis par la mère lors de la grossesse et les anticorps produits par l’enfant à partir de sa naissance. La somme des concentrations de ces deux anticorps est appelée concentration globale en anticorps dans le sang. La concentration en anticorps dans le sang sera exprimée en grammes par litre (g/L).  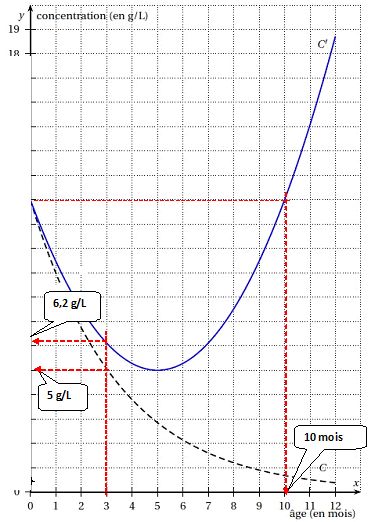Partie A : Étude graphique On a tracé, dans un repère orthogonal du plan : - la courbe C représentative de la fonction f (en tiretés) correspondant à la concentration en anticorps maternels ; - la courbe C′ représentative de la fonction g (en trait plein) correspondant à la concentration globale en anticorps. Pour chacune des questions suivantes, on répondra à l’aide du graphique et on laissera les traits de construction apparents . On arrondira les réponses à l’unité. 1. À quel âge l’enfant retrouve-t-il la même concentration globale en anticorps qu’à la naissance ? 2. Déterminer f (3) et g (3). En déduire la concentration en anticorps produits par l’enfant à l’âge de 3 mois. A l'âge de 3 mois, la concentration d'anticorps produits par l'enfant est de 1,2 g/L. Partie B : Évolution de la concentration en anticorps transmis par la mère. On modélise la concentration en anticorps maternels dans le sang de l’enfant à l’aide de la fonction f définie sur l’intervalle [0 ; 12] par : f (x) = 12×0,75x . Le nombre f (x) représente la concentration en anticorps maternels dans le sang en fonction de l’âge x. 1. On admet que sur l’intervalle [0 ; 12] la fonction f admet le même sens de variation que la fonction u définie par u(x) = 0,75x . Déterminer, en justifiant votre réponse, le sens de variation de la fonction f sur l’intervalle [0 ; 12]. Interpréter ce résultat. Si 0 < a < 1, alors la fonction qui à x associe ax est une fonction strictement décroissante sur R. Dans ce cas a = 0,75, nombre strictement inférieur à 1, en conséquence la fonction x |-->0,75x est une fonction strictement décroissante sur [0 ; 12]. Par suite la fonction f est strictement décroissante sur l’intervalle [0 ; 12]. 2. Calculer la concentration en anticorps maternels dans le sang de l’enfant à l’âge de 3 mois. Arrondir le résultat au centième. f(3) = 12 x 0,753 = 5,06 g/L. 3. Résoudre l’inéquation f (x) <= 9. En déduire l’âge à partir duquel la concentration en anticorps maternels dans le sang est inférieure à 9 g/L. 12×0,75x  <= 9 ; 0,75x  <= 9 /12 ; x log 0,75 <=log ( 9 /12) ; -0,125 x <= -0,125 ; x > 1. Au delà d'un mois la concentration en anticorps maternels dans le sang est inférieure à 9 g/L. Partie C : Évolution de la concentration globale en anticorps dans le sang On modélise la concentration globale en anticorps dans le sang de l’enfant à l’aide de la fonction g définie sur l’intervalle [0 ; 12] par : g (x) = 0,28x2 −2,8x +12. Le nombre g (x) représente la concentration globale en anticorps dans le sang en fonction de l’âge x, exprimé en mois, de l’enfant. 1. Déterminer la fonction dérivée g ′ de la fonction g sur l’intervalle [0 ; 12]. 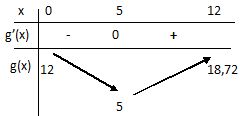g'(x) = 0,56 x -2,8 2. Étudier le signe de la fonction g ′ et en déduire le tableau de variation de la fonction g sur l’intervalle [0 ; 12]. g(0) = 12 ; g(5) = 0,28 x 52 -2,8 x5 +12 = 5 ; g(12) = 0,28 x 122 -2,8 x12 +12 = 18,72. 3. À quel âge la concentration globale en anticorps dans le sang est-elle minimale ? exprimé en mois, de l’enfant. A 5 mois la concentration en anticorps est minimale. Nlle Calédonie. En épidémiologie, on cherche à comprendre comment une maladie se transmet d’un individu à l’autre afin de prédire les épidémies et leur évolution dans le temps au sein d’une population. À l’aide d’un modèle, on va étudier ici l’incidence d’une épidémie sur une population de 5 000 personnes durant 20 jours. Le principe est de diviser la population en 3 catégories (ou compartiments). Chaque individu de la population appartient à une seule catégorie à la fois mais il peut changer de catégorie au cours du temps. La catégorie S désigne l’ensemble des individus Sains (ou susceptibles d’être infectés par la maladie). La catégorie I désigne l’ensemble de ceux qui sont Infectés au sein de la population. La catégorie R désigne l’ensemble de ceux qui sont Rétablis et ne peuvent plus être infectés. On suppose qu’un individu guéri est définitivement immunisé. On a représenté en annexe dans un même repère orthogonal : - la courbe Cs de la fonctions s qui modélise l’évolution du nombre d’individus de la catégorie S en fonction du temps ; - la courbe Cr de la fonction r quimodélise l’évolution du nombre d’individus de la catégorie R en fonction du temps. Partie A. 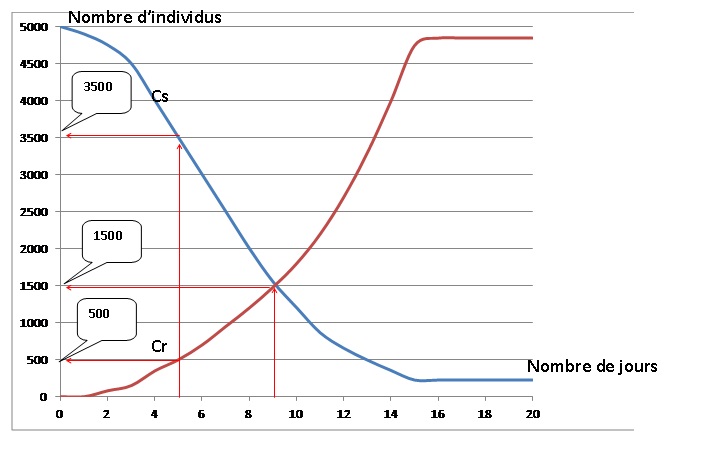1. a. Combien y a-t-il d’individus sains et d’individus rétablis au bout de 5 jours ? Arrondir le nombre de personnes à la centaine. 3500 individus sains et 500 individus rétablis. b. Sachant que chaque individu de la population appartient à une des 3 catégories, en déduire le nombre de personnes infectées au bout de 5 jours d’après ce modèle. 5000 -2500-500) = 4000. 2. Indiquer au bout de combien de jours il y a davantage d’individus rétablis que d’individus sains. Indiquer alors le nombre d’individus rétablis. Au bout de 9 jours et il y a 1000 individus rétablis. 3. Au bout de combien de jours le nombre de personnes saines est-il inférieur à 20% de la population ? 5000 x0,20 = 1000. Au bout de 11 jours, le nombre de personnes saines est inférieur à 1000. Partie B. Dans cette partie, on considère la fonction i définie sur l’intervalle [0 ; 15] par : i (t )= −4t3 +60t2. On admet que i (t ) représente le nombre d’individus infectés par cette maladie dans la population donnée au bout de t jours (avec 0< t <15). 1. Calculer i (5). Faire le lien avec la question 1. de la partie A. i(5) = -4 x53 +60 x52=1000. ( 5000 - nombre d'individus sains -nombre d'individus rétablis = nombre d'individu infectés. 2. a. La fonction i est dérivable sur l’intervalle [0 ; 15] et l’on note i ′ sa fonction dérivée. Montrer que i ′(t ) = 12t (−t +10). i'(t) = -12t2 +120t =12t (-t+10) b. Reproduire et compléter le tableau de signes ci-dessous : c. En déduire le tableau de variation de la fonction i sur l’intervalle [0 ; 15]. 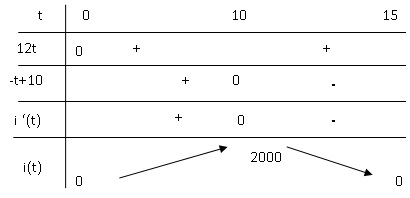i(t) est strictement croissante sur [0 ; 10[ ; i(t) est strictement décroissante sur ]10 ; 15] 3. Combien de personnes sont-elles infectées par la maladie au plus fort de l’épidémie ? Justifier la réponse. i(t) présente un maximum égal à 2000 pour t = 10 jours.

menu