Mathématiques,
bac ST2S Antilles 2017.
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Le
tableau suivant provient de données statistiques sur les accidents
cyclistes en
France métropolitaine en 2008 :
Age
|
Blessés
hospitalisés
|
Blessés
non hospitalisés
|
0
- 14 ans
|
275
|
383
|
15
- 24 ans
|
245
|
611
|
25
- 44 ans
|
337
|
965
|
45
- 64 ans
|
458
|
669
|
65
ans ou +
|
224
|
219
|
Total
|
1539
|
2847
|
Source : fubicy.org.
Partie A : on
arrondira les résultats à 0,1%
1. Parmi les
blessés suite à un accident de vélo en France métropolitaine en 2008,
déterminer le pourcentage de personnes hospitalisées.
1539 x100 / (2847+1539)=35,1 %.
2. Parmi les
blessés hospitalisés suite à un accident de vélo en France
métropolitaine en 2008, déterminer le pourcentage de personnes âgées de
45 à 64 ans.
458 x100 / 1539=29,8 %.
3. Parmi les 15 à
24 ans blessés suite à un accident de vélo en France métropolitaine en
2008, déterminer le pourcentage de blessés non hospitalisés.
611 x 100 / (611+245)=71,4 %.
4. Les accidents
sont considérés comme graves lorsque les blessés sont hospitalisés.
Un article affirme : « À partir de 25 ans, la gravité des accidents
cyclistes augmente avec l’âge ».
Cette affirmation vous semble-t-elle vraie au vu des données de
l’énoncé ? Justifier la réponse.
Pourcentage de blessés hospitalisés en fonction de l'âge :
25 - 44 ans : 337 x100 /(337 +965) =25,9 %.
45 - 64 ans : 458 x100 /(458 +669) =40,6 %.
65 ans ou + : 224 x100 /(224 +219) =50,6 %.
L'affirmation est vraie.
Partie B : on
arrondira les résultats à 0,01 près
On contacte au hasard une personne blessée suite à un accident de vélo
en France métropolitaine en 2008. On définit les évènements suivants :
H : « La personne contactée a été hospitalisée »
A : « La personne contactée a entre 25 et 44 ans »
B : « La personne contactée a 45 ans ou plus »
1. Calculer la
probabilité des évènements H, A et B.
p(H) = 1539 / (1539+2847)=0,35.
p(A) = (337 + 965) / (1539+2847)=0,30.
p(B) = (458+669+224+219)/(1539+2847)=0,36.
2. Définir
l’évènement H n A par une phrase puis calculer sa probabilité.
La personne a été hospitalisée et a entre 25 et 44 ans.
p(H n A)=337 /(1539+2847)=0,0768 ~0,08.
3. Calculer la
probabilité que la personne contactée soit âgée de 45 ans ou plus
sachant qu’elle a été hospitalisée.
p(H n
B)=(458+224) /(1539+2847)=0,155.
pH(B) = p(B n H) / p(H) =0,155 / 0,35 ~0,44.
|
....
.....
|
Exercice
2. (8 points)
Les
tableaux ci-dessous donnent, pour certaines années, l’espérance de vie,
en années, des femmes et des hommes à divers âges en France (hors
Mayotte).
|
Espérance de vie des
femmes
|
Année
|
à
0 an
|
à
20 ans
|
à
60 ans
|
1995
|
81,9
|
62,5
|
24,9
|
2000
|
82,8
|
63,4
|
25,6
|
2005
|
83,8
|
64,3
|
26,4
|
2010
|
84,6
|
65,1
|
27,1
|
.
|
Espérance de vie des
hommes
|
Année
|
à
0 an
|
à
20 ans
|
à
60 ans
|
1995
|
73,8
|
54,7
|
19,7
|
2000
|
75,2
|
56,0
|
20,4
|
2005
|
76,7
|
57,4
|
21,4
|
2010
|
78,0
|
58,6
|
22,4
|
Source Insee.
Par
exemple, en 1995,
une femme de 20 ans vivant en France (hors Mayotte) avait une espérance
de vie restante de 62,5 années. Cela signifie qu’il était estimé en
1995 que les femmes de 20 ans vivraient, en moyenne, jusqu’à 82,5 ans.
Partie A : Étude de
l’espérance de vie des hommes de 60 ans.
1. D’après les
indications du tableau, en 2010, quelle était l’espérance de vie
restante d’un homme de 60 ans ? 22,4
ans.
2. a. Calculer le
pourcentage d’évolution, à 0,1% près, entre l’espérance de vie restante
en 1995 d’un homme de 60 ans et l’espérance de vie restante en 2010
d’un homme de 60 ans.
(22,4-19,7) x100 /19,7 ~13,7 %.
b. Comparer ce
pourcentage d’évolution de l’espérance de vie restante des hommes de 60
ans à celui des femmes de 60 ans, sur la même période.
Cas des femmes : (27,1-24,9) x100 / 24,9 ~8,83 %.
L'espérance de vie des hommes s'est plus accru que celui des femmes sur
cette période.
3. L’espérance de
vie restante des hommes de 60 ans a augmenté de 5% entre 2010 et 2015.
En apprenant cette bonne nouvelle, Jacques, un homme de 60 ans en 2015
affirme : « les hommes de ma génération peuvent légitimement espérer
vivre jusqu’à 83 ans et demi ! ». Justifier les propos de Jacques.
22,4 x1,05 = 23,52.
60+23,52 ~83,5 ans. L'affirmation est vraie.
Partie B : Étude de l’espérance de
vie à la naissance
L’espérance de vie à 0 an est aussi appelée espérance de vie à la
naissance.
1. Espérance de vie
à la naissance des femmes
a. Représenter le
nuage de points de coordonnées (x ; y) où x représente l’année de
naissance et y
représente l’espérance de vie des femmes à la naissance, selon le
tableau de l’Insee.
b. Calculer les
coordonnées du point moyen G de ce nuage de points et placer G sur le
graphique.
c. La forme du
nuage de points montre qu’un ajustement affine est pertinent.
Un logiciel donne y = 0,182x −281,18 comme équation de la droite qui
réalise au mieux cet ajustement. Tracer cette droite sur le graphique.
d. D’après cet
ajustement, trouver graphiquement l’espérance de vie prévisible à la
naissance des femmes qui naîtront en 2020.
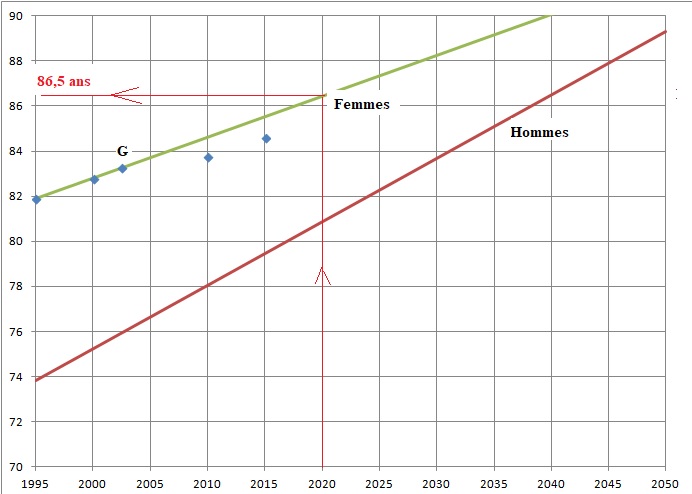
xG=(1995 +2000 +2005 +2010) / 4 = 2002,5.
yG = ( 81,9+82,8+83,8+84,6)/4=83,275.
2. Comparaison de
l’espérance de vie des femmes et de celle des hommes à la naissance
De manière similaire, un ajustement affine est pertinent pour le nuage
de points (x ; y) où x représente l’année de naissance et y représente
l’espérance de vie à la naissance des hommes, selon le tableau de
l’Insee.
Un logiciel donne y = 0,282x −488,78 comme équation de la droite qui
réalise au mieux cet ajustement.
Pour cette dernière question, on estime que les ajustements affines
proposés dans cet exercice sont fiables jusqu’en 2050. À partir de
cette hypothèse, peut-on en déduire qu’en 2050, l’espérance de vie à la
naissance des hommes dépassera celle des femmes ? Justifier la réponse.
En cas d'espérance de vie identique :
0,282x −488,78 = 0,182x
−281,18.
(0,282-0,182)x = 488,78-281,18 ; 0,1 x =207,6 ; x=2076.
L'espérance de vie des hommes sera égale à celle des femmes en 2076 et
non pas en 2050.
|
|
|
Exercice
3.
Partie A :
Une dose d’un médicament est injectée dans le sang par piqûre
intraveineuse. On suppose que le médicament se répartit instantanément
dans le sang et que sa concentration initiale dans le sang est égale à
85 mg/L. On admet que le corps élimine chaque heure 25% du médicament.
On considère la suite (Cn) où Cn désigne la
concentration en mg/L de médicament dans le sang n heures après
l’injection avec n désignant un entier naturel. On a ainsi C0
= 85 mg/L.
1. Calculer C1
et C2. Arrondir à 0,01. Interpréter ces deux résultats.
C1 = C0 x(1-0,25) = 85 x0,75=63,75 mg/L.
Une heure après l'injection, la concentration en médicament dans le
sang est égale à 63,75 mg /L.
C2
= C1 x(1-0,25) = 63,75 x0,75=47,81
mg/L.
Deux heures après l'injection, la concentration en médicament dans le
sang est égale à 47,81 mg /L.
2.
Montrer que la suite (Cn) est une suite géométrique dont on
précisera la raison et le premier terme.
On passe d'un terme au suivant en le multipliant par 0,75. La
suite est géométrique de premier terme 85 et de raison : 0,75.
3. Pour calculer à
chaque heure la concentration de médicament présente dans le sang, on
utilise un tableur. La feuille de calcul est reproduite.
Quelle formule à recopier vers le bas, faut-il saisir dans la cellule
B3 pour obtenir les premières valeurs de la suite (Cn) ?
|
A
|
B
|
1
|
n
|
Cn
|
2
|
0
|
85
|
3
|
1
|
|
4
|
2
|
|
5
|
3
|
35,86
|
=B2*0,75
4. Exprimer Cn
en fonction de n. En déduire la concentration demédicament dans le sang
au bout de 14 heures. Arrondir à 0,01.
Cn = 85 x0,75n.
C14 = 85 x0,7514 =1,51
mg/L.
|
|
|
|
Partie B :
Pour avoir des résultats plus précis, on admet que la concentration en
mg/L de médicament dans le sang t heures après l’injection peut être
modélisée par la fonction G définie sur [0; 19] par :
G(t )= 85×0,75t .
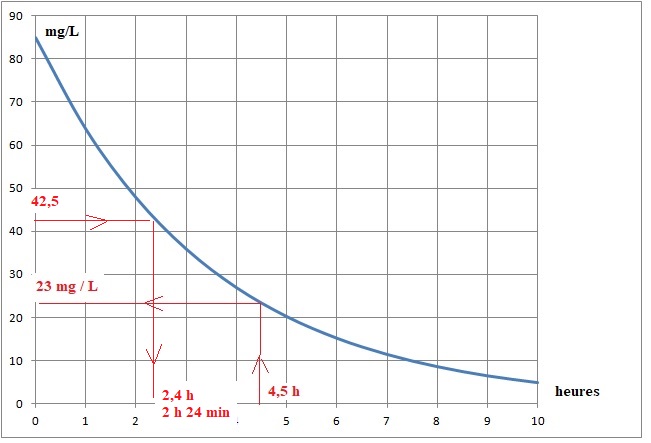
La courbe représentative de la fonction G est tracée.
1. Par lecture
graphique, avec la précision permise par le graphique, déterminer :
a. La concentration
demédicament présente dans le sang au bout de 4 heures et 30 minutes.
b. Le temps à
partir duquel la concentration de médicament dans le sang est
inférieure à 50% de la concentration initiale.
2. Déterminer par
le calcul une valeur approchée à 0,1 heure près du temps t0 à
partir duquel la concentration de médicament dans le sang est
inférieure à 20% de la concentration initiale, puis exprimer cette
valeur approchée en heures et minutes.
85 x0,20=17 mg/L.
17 = 85 x0,75t ;
ln 17 = ln 85 +t ln 0,75 ;
ln17-ln75 = t ln0,75 ;
-1,609 = -0,2876 t ;
t0 ~5,6 h ou 5 h 36
min.
|
|