Mathématiques,
bac
ST2S Polynésie 2017 .
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice 1. QCM ( 5 points)
1. Après une
campagne de vaccination contre une maladie, on constate que le nombre
de malades
a diminué de 25% la première année et de 12% la seconde. Le pourcentage
de baisse du nombre de malades à la fin de la deuxième année est égal à
:
a. 40% ; b. 34% ; c. 37% ; d.
66%.
Prix payé au bout d'une année pour un prix affiché de 100 € : 75 € ;
baisse 25 €.
Baisse lors de la seconde année : 75 x 0,12 = 9 € ; baisse totale : 25
+9 = 34 € soit 34 %.
2. On considère la
suite géométrique (v n) de raison 2 telle que v 5 =
96. Alors v 0 est égal à :
a. 86 ; b. 3 ; c. 96×25 ; d.
32.
v 5 = v 0 x2 5 ; v 0 = v 5
/2 5=96 / 32 =3.
Pour les trois questions suivantes, on considère la suite arithmétique
(u n) de premier terme u 0 = 3 et de
raison 2,4.
3. Alors u 20
est égal à :
a. 62,4 ; b. 108 ; c. 48 ; d. 51.
u 20 =u 0 +20 x2,4 =3+ 48 =51.
4. On utilise une
feuille de calcul pour déterminer les termes de la suite (un).
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
2
|
un
|
3
|
5,4
|
|
|
|
|
|
|
3
|
Sn
|
3
|
8,4
|
|
|
|
|
|
|
Quelle formule a-t-on entrée dans la cellule C2 qui, recopiée vers la
droite, permet de calculer les
termes successifs de la suite (u n) ?
a. =$B$2+2,4 ; b. = B2+2,4 ; c.
=$B2+2,4 ; d. =B2*2,4.
5. On souhaite
calculer la somme S 7 = u 0+u 1+· · ·+u 7
des 8 premiers termes de!a suite (u n). Quelle
formule a-t-on entrée dans la cellule C3 qui, recopiée vers la droite,
permet de calculer S7 ?
a. =B3+C3 ; b. =Somme(B2 :C2) ; c. = C2+B3
; d. =B2+C2.
Exercice 2. (7
points)
Le tableau ci-dessous montre l’évolution du nombre de places
disponibles en première année d’IFSI
(Institut de Formation en Soins Infirmiers) ainsi que le nombre de
candidats admis à l’issue des épreuves
dans un département de France.
Session
|
2008
|
2009
|
2010
|
2011
|
2015
|
2013
|
Nombre
de places disponibles
|
590
|
607
|
615
|
617
|
620
|
614
|
Nombre
d'étudiants admis
|
507
|
521
|
533
|
536
|
541
|
542
|
1. Calculer la
proportion d’étudiants admis par rapport au nombre de places
disponibles pour la
session 2013. Donner le résultat sous forme de pourcentage arrondi à
0,1%.
542 / 614 x100 ~ 88,3 %.
2. Calculer le taux
d’évolution du nombre d’étudiants admis en 1re année d’IFSI entre les
sessions
des années 2008 et 2013. Donner le résultat sous forme de pourcentage
arrondi à 0,1%.
(542-507) / 507 x100 ~ 6,9 %.
|
....
...
|
3.
On souhaite prévoir le nombre d’étudiants admis pour la session 2018.
On s’appuie sur le tableau suivant :
Session
|
2008
|
2009
|
2010
|
2011
|
2012
|
2013
|
Rang
de l'année (xi)
|
1
|
2
|
3
|
4
|
5
|
6
|
Nombre
d'étudiants admis ( yi)
|
507
|
521
|
533
|
536
|
541
|
542
|
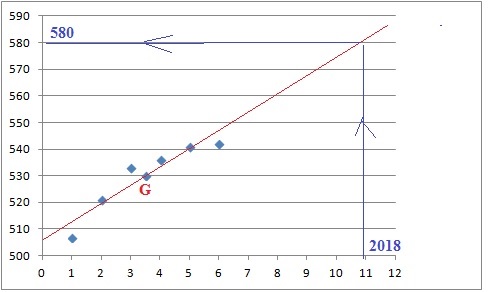
a. Représenter le nuage de points de
coordonnées (xi ; yi )
b. Déterminer les
coordonnées du point moyen G de ce nuage de points et le placer dans le
repère précédent.
xmoyen = (1+2+3+4+5+6) / 6=3,5.
ymoyen = (507+521+533+536+541+542) / 6 =530.
c. On admet que la
droite (D) passant par G et de coefficient directeur 6,8 est une droite
d’ajustement
de ce nuage valable pour les prochaines années.
Montrer que la droite (D) admet pour équation réduite : y = 6,8x +506,2
L'équation de la droite (D) est de la forme y =6,8x+b.
La droite passe par G(3,5 ; 530) ; 530 = 6,8 x3,5 +b ; b = 530-23,8 =
506,2.
d,. Tracer la
droite (D) dans le repère précédent.
e. À
l’aide de cet ajustement, calculer le nombre prévisionnel d’étudiants
admis en 2018. Retrouver le résultat par lecture graphique en laissant
les traits de construction apparents.
Rang de l'année 2018 : x = 11 ; y = 6,8 x11 +506,2 = 581.
Exercice 3. ( 9
points).
Chaque semaine, le réseau Sentinelles collecte auprès de ses médecins
des informations permettant
notamment d’estimer le nombre de cas de certaines maladies (grippe,
varicelle, oreillons, etc.) sur une
période donnée.
Ainsi, on a évalué, pendant 15 semaines, à partir de mi-novembre 2014,
le nombre de personnes présentant des syndromes grippaux.
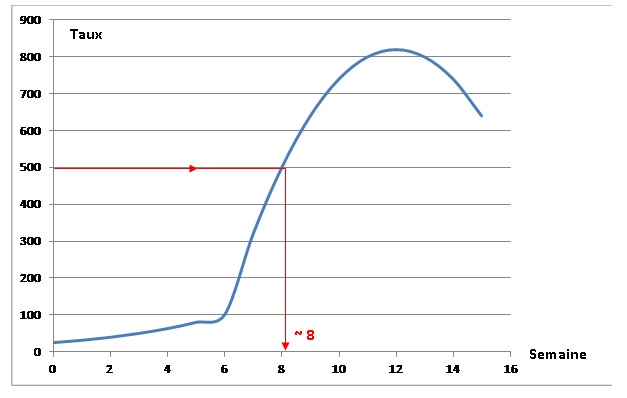
La courbe ci-dessous donne l’évolution du taux d’incidence de la grippe
(nombre de cas grippaux
observés pour 100 000 habitants) pendant la période considérée.
Partie A :
Première phase d’évolution
Pendant les 6 premières semaines d’observation, le taux d’incidence de
la grippe est modélisé par la
fonction f définie sur l’intervalle [0 ; 6] par : f (t ) = 24×1,27t
, où t est le nombre de semaines écoulées
depuis le début de l’observation.
1. Calculer le taux
d’incidence de la grippe au bout de la 1ére semaine
d’observation.
Donner la valeur exacte de ce taux d’incidence.
f(1) = 24 x1,27 =30,48.
2. On admet que la
fonction f a le même sens de variation que la fonction g définie sur
l’intervalle
[0; 6] par : g (t ) = 1,27t . Indiquer, en justifiant, le
sens de variation de la fonction g , puis celui de la fonction f , sur
l’intervalle [0 ; 6].
1,27 étant strictement supérieur à 1,la fonction g(t) est strictement
croissante sur [0 ; 6].
f(t) = 24 g(t) , produit de g(t) par un nombre positif, est donc
strictement croissante sur [0 ; 6 ].
3. a. Résoudre
l’inéquation : 24×1,27t > 60,96.
ln24 +t ln1,27 > ln60,96 ;
t ln(1,27) > ln 60,96 -ln 24 ; t > (ln60,96 -ln 24) / ln 1,27 ;
t > ln( 60,96 / 24) /ln 1,27 ; t >ln 2,54 / ln 1,27.
b. Au bout de
combien de semaines écoulées le taux d’incidence de la grippe
dépassera-t-il le double du taux d’incidence observé au bout de la
première semaine ?
24 x1,27t > 30,48 x2 ; 1,27t > 30,48 x2 /
24 ; 1,27 t >2,54 ;
t ln 1,27 > ln 2,54 ; t > ln 2,54 / ln 1,27.
ln 2,54 / ln 1,27. ~3,9 soit 4 semaines.
|
|
|
Partie
B : Deuxième phase d’évolution
Au-delà de la 6è semaine d’observation,
on modélise le taux d’incidence par la fonction h définie sur
l’intervalle ]6 ; 15] par : h(t ) = −20t 2 +480t −2059,3.
1. Déterminer à
l’aide du graphique, au bout de combien de semaines écoulées le taux
d’incidence
dépasse 500 pour la première fois. (On laissera apparents les traits
nécessaires à la lecture).
|
|
|
|
2. a. Déterminer h′(t ) où h′ est
la fonction dérivée de la fonction h sur l’intervalle ]6 ; 15] .
b. Étudier le signe
de h′(t ) en fonction de t sur l’intervalle ]6 ; 15].
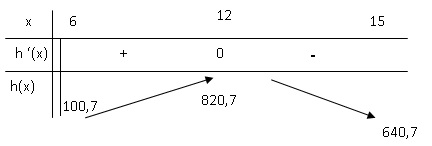
c. En déduire le
tableau de variation de la fonction h sur l’intervalle ]6 ; 15].
h '(t) = -40t +480.
h '(t) = 0 si t = 480 / 40 =12.
h '(t) est strictement positive si t est compris entre ]6 ; 12[ et h(t)
est strictement croissante sur cet intervalle.
h '(t) est strictement négative si t est compris entre ]12 ; 15[ et
h(t) est strictement décroissante sur cet intervalle.
h'(t) est nulle si t=12 et h(t) présente un maximum pour t = 12.
3. Pendant la
deuxième phase d’évolution, à quel moment le taux d’incidence de la
grippe est-il le plus élevé ? Quelle valeur maximale atteint-il ?
A t = 12 semaines, le taux d'évolution de la grippe est le plus élevé ;
il atteint la valeur 820,7.
|
|