Mathématiques, bac
ST2S, Métropole 09 /2017
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Exercice 1. 7 points
La Caisse Nationale des Allocations Familiales (CNAF) établit des
statistiques portant sur les dossiers des foyers allocataires de
prestations familiales.
Le tableau ci-dessous présente la répartition des dossiers des foyers
allocataires selon le nombre d’enfants au sein du foyer et le lieu de
résidence en 2014 :
Nombre d'enfants
|
Nombre de foyers
allocataires ( en milliers)
|
Métropole
|
Outre
mer
|
Total
|
1
|
1944
|
145
|
2089
|
2
|
6255
|
211
|
6466
|
3
|
3263
|
124
|
3387
|
4
|
996
|
58
|
1054
|
5
ou plus
|
461
|
62
|
523
|
Total
|
12919
|
600
|
13519
|
(Source : CNAF fichier FILEAS)
On choisit au
hasard et de manière équiprobable le dossier d’un foyer allocataire. On
considère les évènements suivants :
M : « Le dossier choisi est celui d’un foyer allocataire habitant en
métropole » ;
E : « Le dossier choisi est celui d’un foyer allocataire avec 5 enfants
ou plus ».
Dans cet exercice, les résultats seront arrondis au millième.
1. a. Calculer la
probabilité de choisir le dossier d’un foyer allocataire habitant en
métropole.
p(M) = 12919 / 13 519 ~ 0,956.
b. Calculer la
probabilité de l’évènement E.
p(E) =523 / 13 519 ~0,03867 ~ 0,039.
c. Décrire par une
phrase le contraire de l’évènement E puis calculer sa probabilité.
Le dossier choisi est celui d'un allocataire ayant moins de 5 enfants.
1-0,03867 ~ 0,961.
2. a. Décrire par
une phrase l’évènement M n E puis calculer sa probabilité.
Le dossier
choisi est celui d’un foyer allocataire habitant en métropole avec 5
enfants ou plus.
461 / 13519 ~0,034.
b. Calculer
la probabilité de choisir le dossier d’un foyer allocataire habitant
dans les départements
d’outre-mer et ayant 5 enfants ou plus.
62 /13519 ~0,00458 ~ 0,005.
3. a. Déterminer P M(E).
P M(E) = p(M n E) / p(M) = 461 / 12919 ~ 0,036.
b. Déterminer la
probabilité de choisir le dossier d’un foyer allocataire ayant 5
enfants ou plus
sachant que le dossier est celui d’un foyer allocataire habitant dans
les départements d’outre mer.
62 / 600 ~ 0,103.
4.
La probabilité de choisir le dossier d’un foyer allocataire avec 5
enfants ou plus est-elle plus importante parmi les foyers allocataires
habitant en métropole ou parmi ceux des départements
d’outre-mer ? Justifier la réponse à l’aide des résultats précédents.
PM(E) =0,036,
inférieur à 0,103.
La
probabilité de choisir le dossier d’un foyer allocataire avec 5
enfants ou plus est moins importante parmi les foyers allocataires
habitant en métropole.
|
....
...
|
Exercice 2.
5 points
Le tableau ci-dessous indique le nombre total de mariages enregistrés
en France entre 2001 et 2014.
Année
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
Rang
de l'année xi
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Nombre
de marriages ( milliers) yi
|
297
|
286
|
283
|
279
|
282
|
273
|
273
|
| Année |
2008
|
2009
|
2010
|
2011
|
2012
|
2013
|
2014
|
| Rang de
l'année xi |
8
|
9
|
10
|
11
|
12
|
13
|
14
|
| Nombre
de marriages ( milliers) yi |
264
|
251
|
252
|
238
|
245
|
239
|
241
|
(source : d’après INSEE)
Le nuage de points
de coordonnées (xi ; yi ) associé à ce tableau est
représenté dans le graphique ci-dessous.
1. Calculer les
coordonnées du point moyen G de ce nuage. Arrondir les résultats au
dixième.
Placer ce point dans le repère fourni en annexe.
xm=(1+2+3+4+5+6+7+8+9+10+11+12+13+14) / 14 =7,5
ym=(297+286+283+279+282+273+273+264+251+252+238+245+239+241)
/ 14 =264,5.
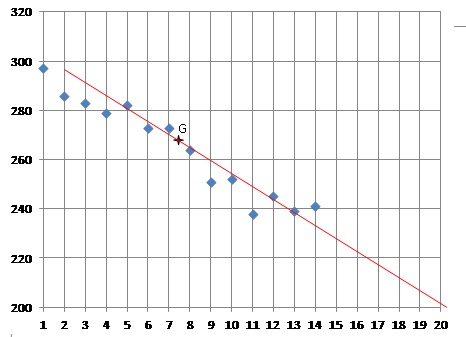
On considère les points A(1 ; 297) et B(10 ; 252). On modélise le
nombre de mariages par an en France, compté en milliers, par la droite
d’ajustement (AB).
2. Justifier que
l’équation de la droite (AB) est : y = −5x +302.
y = a x +b avec a et b des constantes.
A appartient à la droite (AB) : 297 = a +b ; b = 297-a.
Les coordonnées du point B vérifient l'équation de la droite : 252 = 10
a+b.
252 =10a+297-a ; 9a = -297+252 ; a = -5 ; b = 297+5 = 302.
3. Prouver que le
point G appartient à la droite (AB).
264,5 = -5 x7,5 +302 = 264,5.
Les coordonnées du point G vérifient l'équation de la droite. G
appartient à cette droite.
4. Tracer la
droite (AB) dans le repère .
5. On suppose que
lemodèle reste valable jusqu’en 2025.
a. Donner une
estimation du nombre de mariages en 2017.
x=17 ; y =-5 x17 +302 = 217 milliers.
b. Déterminer
l’année à partir de laquelle le nombre de mariages en France sera
inférieur à
200 000.
-5x +302 < 200 ; -5x < -102 ; x > 302/5 ; x >20,4.
A partir de 2021, le nombre de mariages sera inférieur à 200 000.
|
|
|
Exercice 3.
Partie A.
On étudie dans cette partie l’évolution dumontant annuel des dépenses
consacrées en France aux soins hospitaliers entre 2009 et 2014.
Ce montant est donné dans le tableau ci-dessous, extrait d’une feuille
de calcul automatisé.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
Année
|
2009
|
2010
|
2011
|
2012
|
2013
|
2014
|
2
|
Montant
des dépenses
millards €
|
78,3
|
|
82,4
|
84,5
|
86,6
|
88,6
|
3
|
Pourcentage
annuel d'évolution
|
XX
|
2,4
%
|
2,7
%
|
2,5
%
|
|
|
(Source : INSEE)
1. Déterminer le
pourcentage d’évolution du montant des dépenses, entre l’année 2012 et
l’année
2013. Arrondir le résultat à 0,1%.
(86,6-84,5) / 84,5 x100 ~2,5 %.
2. Déterminer le
montant des dépenses en 2010. Arrondir le résultat au dixième de
milliard d’euros.
(x-78,3) / 78,,3 x100 = 2,4 ;
x-78,3 = 2,4 x78,3 /100 = 1,8792 ; x ~80,2.
3. Les cellules C3
à G3 sont au format pourcentage arrondi à 0,1%.
Proposer une formule à saisir dans la cellule C3 qui, recopiée vers la
droite, permet de calculer,
dans la plage de cellules C3 : G3, le pourcentage d’évolution entre
deux années consécutives du
montant des dépenses.
=(C2-B2)/B2*100
|
|
|
|
Partie B
Dans
cette partie, on modélise lemontant des dépenses consacrées aux soins
hospitaliers à l’aide d’une suite numérique. Pour tout entier naturel
n, on note un l’estimation du montant des dépenses, en
milliards d’euros, pour l’année (2014+n). Ainsi u0 = 88,6.
On suppose que ces dépenses augmenteront de 2,5% par an après 2014.
1. Indiquer, sans
justification, la nature de la suite (un). Donner la valeur
de sa raison.
Suite géométrique de raison 1
+0,025 = 1,025 et de premier
terme u0=88,6.
2. Exprimer un en
fonction de n.
un =
88,6 x1,025n.
3. Calculer u6
(le résultat sera arrondi au dixième). Interpréter la valeur de u6
dans le contexte de l’exercice.
u6 = 88,6 x1,0256 ~102,7.
En 2020, les dépenses de santé s'éleveront à 102,7 milliards d'euros.
4. Résoudre dans
l’ensemble des nombres réels l’inéquation : 88,6×1,025x
>120.
1,025x > 120 /88,6 ; x ln1,025 >ln(120 /88,6).
x > ln(120 / 88,6) / ln1,025 ; x supérieur à 12,28.
5.
Déterminer en quelle année la modélisation prévoit que les dépenses
pour les soins hospitaliers dépasseront 120 milliards d’euros ?
On arrondit x à 13 ;
En 2014 +13 = 2027, les
dépenses seront supérieures à 120 milliards d'euros.
|
|