Etude graphique et
numérique de fonctions,
bac
ST2S 2017 .
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie.
Chaque
semaine, le réseau Sentinelles collecte auprès de ses médecins des
informations permettant
notamment d’estimer le nombre
de cas de certaines maladies (grippe, varicelle, oreillons, etc.) sur
une
période donnée.
Ainsi, on a évalué, pendant 15
semaines, à partir de mi-novembre 2014, le nombre de personnes
présentant des syndromes grippaux.
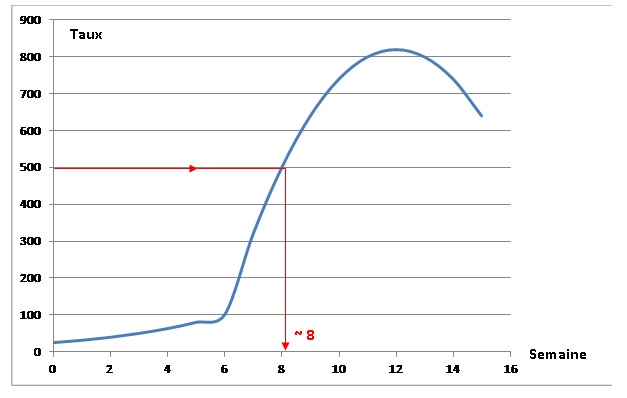
La courbe ci-dessous donne
l’évolution du taux d’incidence de la grippe (nombre de cas grippaux
observés pour 100 000
habitants) pendant la période considérée.
Partie A : Première phase d’évolution
Pendant les 6 premières
semaines d’observation, le taux d’incidence de la grippe est modélisé
par la
fonction f définie sur
l’intervalle [0 ; 6] par : f (t ) = 24×1,27t , où t est
le nombre de semaines écoulées
depuis le début de
l’observation.
1. Calculer le taux d’incidence de la grippe au
bout de la 1ére semaine d’observation.
Donner la valeur exacte de ce
taux d’incidence.
f(1) = 24 x1,27 =30,48.
2. On admet que la fonction f a le même sens de
variation que la fonction g définie sur l’intervalle
[0; 6] par : g (t ) = 1,27t . Indiquer,
en justifiant, le sens de variation de la fonction g , puis celui de la
fonction f , sur l’intervalle [0 ; 6].
1,27 étant strictement
supérieur à 1,la fonction g(t) est strictement croissante sur [0 ; 6].
f(t) = 24 g(t) , produit de
g(t) par un nombre positif, est donc strictement croissante sur [0 ; 6
].
3. a. Résoudre l’inéquation : 24×1,27t > 60,96.
ln24 +t ln1,27 > ln60,96 ;
t ln(1,27) > ln 60,96 -ln 24
; t > (ln60,96 -ln 24) / ln 1,27 ;
t > ln( 60,96 / 24)
/ln 1,27 ; t
>ln 2,54 / ln 1,27.
b. Au bout de
combien de semaines écoulées le taux d’incidence de la grippe
dépassera-t-il le double du taux d’incidence observé au bout de la
première semaine ?
24 x1,27t > 30,48
x2 ; 1,27t > 30,48 x2 / 24 ; 1,27 t >2,54
;
t ln 1,27 > ln 2,54 ; t >
ln 2,54 / ln 1,27.
ln 2,54 / ln 1,27. ~3,9 soit 4 semaines.
Partie
B : Deuxième phase d’évolution
Au-delà de la 6è semaine d’observation,
on modélise le taux d’incidence par la fonction h définie sur
l’intervalle ]6 ; 15] par : h(t ) = −20t 2 +480t −2059,3.
1. Déterminer à
l’aide du graphique, au bout de combien de semaines écoulées le taux
d’incidence
dépasse 500 pour la première fois. (On laissera apparents les traits
nécessaires à la lecture).
|
....
...
|
Métropole.
Partie
A : Étude d’une
fonction.
Soit f la fonction
définie sur l’intervalle [0; 8] par :
f(x)=0,5 x3-12x2+65,625x+20.
1. On note f ' la
fonction dérivée de la fonction f.
Déterminer f '(x) pour
tout réel x appartenant à l’intervalle [0; 8].
f '(x) = 1,5 x2
-24x +65,625.
2. On admet que : f
'(x) =(x-3,5)(1,5x-18,75) pour tout nombre réel x de l’intervalle [0;
8].
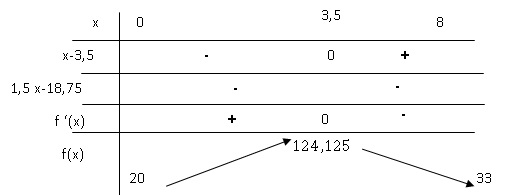
Compléter le tableau de
signes suivant, après l’avoir recopié sur la
copie, afin d’étudier le signe de f '(x) pour x appartenant à
l’intervalle [0; 8].
3. En déduire le
tableau de variation de la fonction sur l’intervalle 0; 8.
On fera apparaître les
valeurs de la fonction f aux bornes de
l’intervalle ainsi qu’aux éventuels changements de variation.
Partie
B : Application.
L'OMS a fixé à 50
milligrammes par litre (mg/L) la concentration limite
de nitrates dans l'eau destinée à la consommation, considérant
qu'au-delà il y a des risques pour la santé.
Suite à un incident
industriel, une importante quantité de nitrates a
été déversée dans un cours d’eau sur lequel se situe un point de
captage pour l’alimentation d’une ville. Un expert indépendant est
alors consulté afin de prévoir l’évolution du taux de nitrates dans ce
cours d’eau au niveau du point de captage pendant les 8 jours suivant
l’incident. L’expert décide de modéliser le taux de nitrates, x jours
après le début de l’incident, à l’aide de la fonction f étudiée en partie A.
1. D’après ce
modèle, quel sera le taux maximal de nitrates atteint pendant la phase
de surveillance de 8 jours ?
124 mg /L.
2. En cas
d’incident, un décret impose de fermer le point de captage pendant 8
jours.
D’après le modèle choisi
par l’expert, sera-t-on au terme des 8 jours
dans les conditions fixées par l’OMS ?
Oui, car f(8) = 33,
valeur inférieure à 50.
|
|
|
Le laboratoire teste l’effet de son antibiotique
sur une colonie de
bactéries pendant une période de 10 heures. Au début du test, la masse
de la colonie est de 500 mg.
Dans cette partie, on modélise l’évolution de la masse de la colonie de
bactéries par la fonction M définie sur l’intervalle [0; 10] par :
M(x) = x3 −9x2 −48x +500
1. Calculer M(0)
et M(10) .
M(0) =500 ; m(10) = 103-9
x100-480+500 =120.
2. On note M′ la
fonction dérivée de la fonction M sur l’intervalle [0;
10].
a. Calculer M′(x).
M'(x) = 3x2-18x-48.
b. Vérifier que,
pour tout x appartenant à l’intervalle [0; 10], M′(x)
= (3x +6)(x −8).
(3x +6)(x −8) = 3x2-24x+6x-48 = 3x2-18x-48.
3. a. Dresser le tableau de signe de
M′(x) sur l’intervalle [0; 10].
b. En déduire le
tableau de variation de la fonction M sur l’intervalle
[0; 10].
4. Quelle est la
valeur du minimum de la fonction M sur l’intervalle [0;
10] ?
f(8) = 83-9 x82 -48x8+500 =52.
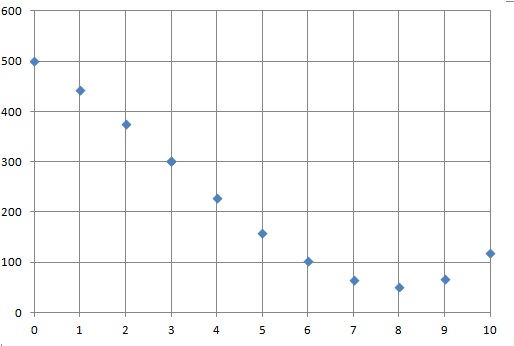
5. L’antibiotique
est dit efficace s’il parvient, au cours du test, à
diviser par cinq la masse initiale de la colonie. L’antibiotique est-il
efficace? Justifier la réponse.
500 / 5 = 100.
L'antibiotique parvient à réduire à moins de 100 le nombre de bactéries
au bout de 6 heures. Il est efficace.
|
|