QCM, nuage de
points, suites,
bac
ST2S 2017 .
|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie.
1. Après une campagne de vaccination contre une
maladie, on constate que le nombre de malades
a diminué de 25% la première
année et de 12% la seconde. Le pourcentage
de baisse du nombre de malades à la fin de la deuxième année est égal à
:
a. 40% ; b. 34% ; c. 37% ; d. 66%.
Prix payé au bout d'une année
pour un prix affiché de 100 € : 75 € ; baisse 25 €.
Baisse lors de la seconde année
: 75 x 0,12 = 9 € ; baisse totale : 25 +9 = 34 € soit 34 %.
2. On considère la suite géométrique (vn) de raison 2
telle que v5 = 96. Alors v0 est égal à :
a. 86 ; b. 3 ; c. 96×25 ; d. 32.
v5 = v0 x25 ; v0 = v5 /25=96 / 32 =3.
Pour les trois questions
suivantes, on considère la suite arithmétique (un) de premier
terme u0 = 3 et de
raison 2,4.
3. Alors u20 est égal à :
a. 62,4 ; b. 108 ; c. 48 ; d. 51.
u20 =u0 +20 x2,4 =3+
48 =51.
4. On utilise une feuille de calcul pour déterminer
les termes de la suite (un).
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
2
|
un
|
3
|
5,4
|
|
|
|
|
|
|
3
|
Sn
|
3
|
8,4
|
|
|
|
|
|
|
Quelle formule a-t-on entrée
dans la cellule C2 qui, recopiée vers la droite, permet de calculer les
termes successifs de la suite (un) ?
a. =$B$2+2,4 ; b. =B2+2,4 ; c. =$B2+2,4 ; d. =B2*2,4.
5. On souhaite calculer la somme S7 = u0+u1+· · ·+u7 des 8
premiers termes de!a suite (un). Quelle
formule a-t-on entrée dans la
cellule C3 qui, recopiée vers la droite, permet de calculer S7 ?
a. =B3+C3 ; b. =Somme(B2 :C2) ;
c. =C2+B3 ; d. =B2+C2.
|
....
...
|
Métropole.
Une municipalité a ouvert au public, en novembre 2016, un parc composé
d’un étang, d’un arboretum et d’une maison de la nature permettant
d’accueillir des expositions de sensibilisation à la protection de
l’environnement.
Pour des raisons de sécurité, la mairie devra affecter à ce parc un
agent supplémentaire si le nombre de visiteurs dépasse 2500 personnes
par mois.
Partie A :
ajustement affine
Afin d’anticiper le recrutement de l’agent supplémentaire, la
municipalité a étudié la fréquentation du parc depuis son ouverture.
Ces données sont regroupées dans le tableau suivant :
Mois
|
Novembre
2016
|
Décembre
2016
|
Janvier
2017
|
Février
2017
|
Mars
2017
|
Avril
2017
|
Mai
2017
|
Rang
du mois (xi)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
Nombre
de visiteurs
par mois ( yi)
|
1200
|
1233
|
1316
|
1360
|
1448
|
1457
|
1520
|
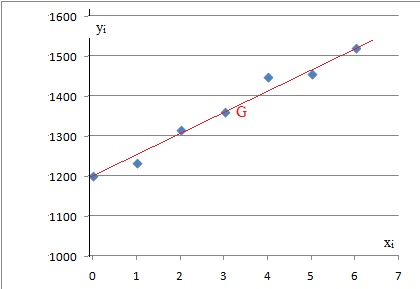
1. Déterminer les coordonnées du
point moyen G de ce nuage (on arrondira, si nécessaire, les
résultats à l’unité). Placer ce point dans le repère
xG=(1 +2 +3 +4 +5 +6) / 7=3.
yG=(1200 +1233 +1316 +1360 +1448 +1457 +1520) / 7=1362.
2. On
fait l’hypothèse que le nombre de visiteurs par mois de ce parc est
correctement
modélisé à l’aide de la droite d’ajustement D d’équation : y = 54
x+1200 ,
x représentant le rang du mois depuis l’ouverture.
a. Tracer la droite
D dans le repère. Préciser les points utilisés pour la construction.
Point (0 ; 1200) et point (6 ; 1524 ).
b. En supposant cet
ajustement fiable jusqu’en 2020, déterminer la date (mois, année) à
partir de laquelle la municipalité devra affecter un agent
supplémentaire à ce parc.
54 x +1200 >2500 ; x > (2500-1200) / 54 ; x >
24,07.
soit 2 ans et 1 mois ; date décembre 2018.
|
|
|
Partie
B : étude de l’impact d’une campagne de communication à l’aide d’une
suite.
La municipalité met en place une campagne de communication et prévoit
que le nombre de visiteurs du parc augmentera de 5% chaque mois à
partir de mai 2017.
On modélise dans cette partie le nombre mensuel de visiteurs du parc à
l’aide d’une suite
(un). Ainsi u0 représente le nombre de visiteurs
en mai 2017 (u0= 1520), u1 représente le
nombre de visiteurs en juin 2017, etc.
Afin d’étudier l’évolution de la fréquentation du parc, la municipalité
utilise la feuille decalcul automatisé suivante :

1. Quelle formule
peut-on entrer dans la cellule C2 de sorte que, recopiée vers la droite
sur la
plage C2:H2, elle permette d’afficher les estimations du nombre de
visiteurs par mois ?
=B2*1,05
2. Utilisation de
la suite (un).
a. Déterminer une
estimation du nombre de visiteurs en juin 2017.
b. Indiquer, sans
justification, la nature de la suite (un). Donner la valeur
de sa raison.
Suite géométrique de premier terme u0
= 1520 et de raison 1,05.
c. Exprimer un
en fonction de n, pour tout entier
naturel
un = u0 x1,05n = 1520 x1,05n.
d. Déterminer une
estimation du nombre de visiteurs dans ce parc en octobre 2017.
n = 5 ; u5 = 1520 x1,055 =1940.
3. Résoudre dans
l’ensemble des nombres réels l’inéquation : 1520 * 1,05x > 2500.
ln 1520 + x ln 1,05 >
ln 2500 ;
x >( ln2500
-ln1520 ) / ln1,05 ; x > 10,19.
4. Déterminer la
date (mois, année) de recrutement d’un agent supplémentaire pour ce
parc, suite à la campagne de communication.
A partir de n = 11, avril 2018.
|
|
|
|
Métropole septembre.
Le tableau ci-dessous indique le nombre
total de mariages enregistrés en France entre 2001 et 2014.
Année
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
Rang
de l'année xi
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
Nombre
de marriages ( milliers) yi
|
297
|
286
|
283
|
279
|
282
|
273
|
273
|
| Année |
2008
|
2009
|
2010
|
2011
|
2012
|
2013
|
2014
|
| Rang
de l'année xi |
8
|
9
|
10
|
11
|
12
|
13
|
14
|
| Nombre
de marriages ( milliers) yi |
264
|
251
|
252
|
238
|
245
|
239
|
241
|
(source : d’après INSEE)
Le nuage de points
de coordonnées (xi ; yi ) associé à ce tableau est
représenté dans le graphique ci-dessous.
1. Calculer les
coordonnées du point moyen G de ce nuage. Arrondir les résultats au
dixième.
Placer ce point dans le repère fourni en annexe.
xm=(1+2+3+4+5+6+7+8+9+10+11+12+13+14) / 14 =7,5
ym=(297+286+283+279+282+273+273+264+251+252+238+245+239+241)
/ 14 =264,5.
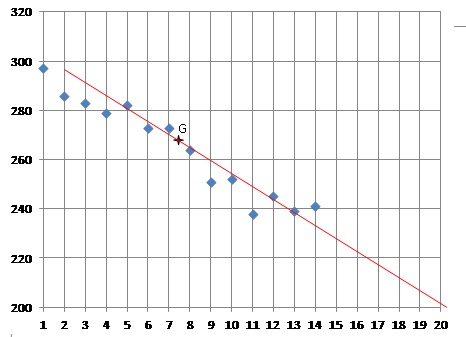
On considère les points A(1 ; 297) et B(10 ; 252). On modélise le
nombre de mariages par an en France, compté en milliers, par la droite
d’ajustement (AB).
2. Justifier que
l’équation de la droite (AB) est : y = −5x +302.
y = a x +b avec a et b des constantes.
A appartient à la droite (AB) : 297 = a +b ; b = 297-a.
Les coordonnées du point B vérifient l'équation de la droite : 252 = 10
a+b.
252 =10a+297-a ; 9a = -297+252 ; a = -5 ; b = 297+5 = 302.
3. Prouver que le
point G appartient à la droite (AB).
264,5 = -5 x7,5 +302 = 264,5.
Les coordonnées du point G vérifient l'équation de la droite. G
appartient à cette droite.
4. Tracer la
droite (AB) dans le repère .
5. On suppose que
lemodèle reste valable jusqu’en 2025.
a. Donner une
estimation du nombre de mariages en 2017.
x=17 ; y =-5 x17 +302 = 217 milliers.
b. Déterminer
l’année à partir de laquelle le nombre de mariages en France sera
inférieur à
200 000.
-5x +302 < 200 ; -5x < -102 ; x > 302/5 ; x >20,4.
A partir de 2021, le nombre de mariages sera inférieur à 200 000.
Dans
cette partie, on modélise lemontant des dépenses consacrées aux soins
hospitaliers à l’aide d’une suite numérique. Pour tout entier naturel
n, on note un l’estimation du montant des dépenses, en
milliards d’euros, pour l’année (2014+n). Ainsi u0 = 88,6.
On suppose que ces dépenses augmenteront de 2,5% par an après 2014.
1. Indiquer, sans
justification, la nature de la suite (un). Donner la valeur
de sa raison.
Suite géométrique de raison 1
+0,025 = 1,025 et de premier
terme u0=88,6.
2. Exprimer un en
fonction de n.
un =
88,6 x1,025n.
3. Calculer u6
(le résultat sera arrondi au dixième). Interpréter la valeur de u6
dans le contexte de l’exercice.
u6 = 88,6 x1,0256 ~102,7.
En 2020, les dépenses de santé s'éleveront à 102,7 milliards d'euros.
4. Résoudre dans
l’ensemble des nombres réels l’inéquation : 88,6×1,025x
>120.
1,025x > 120 /88,6 ; x ln1,025 >ln(120 /88,6).
x > ln(120 / 88,6) / ln1,025 ; x supérieur à 12,28.
5.
Déterminer en quelle année la modélisation prévoit que les dépenses
pour les soins hospitaliers dépasseront 120 milliards d’euros ?
On arrondit x à 13 ;
En 2014 +13 = 2027, les
dépenses seront supérieures à 120 milliards d'euros.
|
|