Exercice 1.
La corpulence est mesurée à partir de l’indice de masse corporelle
(IMC) qui est égal au
rapport entre la masse (en kilogramme) et le carré de la taille (en
mètre). Les individus dont
l’IMC est supérieur à 30 sont considérés comme obèses.
On a réalisé en 2006 une étude à l’aide de questionnaires sur une
population d’individus âgés
de 21 à 59 ans.
Partie A.
Dans cette partie, on choisit un questionnaire au hasard parmi ceux des
femmes interrogées.
On note E l’événement : « le questionnaire choisi correspond à une
personne ayant un emploi ».
On note O l’événement : « le questionnaire choisi correspond à une
personne considérée
comme obèse ».
Selon les données de 2006, on sait que :
- l’effectif total des femmes interrogées est de 2685, dont 1920 ont un
emploi ;
- 10,6% des femmes interrogées sont considérées comme obèses ;
- parmi les femmes considérées comme non obèses, 72,7% ont un emploi.
1. On arrondira les
résultats à l’entier le plus proche.
a. Justifier que le
nombre total de femmes considérées comme obèses est égal à 285 et
que les femmes considérées comme non obèses et ayant un emploi sont au
nombre de 1745.
2685 x 0,106 =284,61 ~
285.
2685-285 =2400 ; 2400 x 0,727 = 1744,8 ~
1725.
b. Compléter le
tableau suivant..
|
Obèse
|
Non
obèse
|
Total
|
Ayant
un emploi
|
1920-1745=175
|
1745
|
1920
|
N'ayant
pas un emploi
|
285-175
=110
|
655
|
765
|
Total
|
285
|
2400
|
2685
|
2. Dans les
questions suivantes, les résultats seront arrondis au millième.
a. Calculer la
probabilité de l’événement E
P(E) = 1920 /2685 ~
0,715.
b. Calculer la
probabilité de l’événement O
P(O) =285 / 2685 ~
0,106.
c. Décrire par une
phrase l’événement E n O et calculer la probabilité de cet événement.
Femmes obèses ayant un emploi.
P(E n O) = 175 / 2685 ~
0,065.
d. Justifier que
les événements E et O ne sont pas indépendants.
P(E) x P(O ) = 0,715 x0,106 ~0,076, valeur différente de
P(E n O).
3. Étude de
l’influence de la corpulence sur le taux d’emploi des femmes en 2006
(les
probabilités seront arrondies au millième).
a. Calculer la
probabilité que le questionnaire choisi corresponde à une femme ayant un
emploi sachant qu’elle est considérée comme obèse.
P
O(E) =175 / 285 ~
0,614.
b. Déterminer la
probabilité suivante.
Le
questionnaire choisi corresponde à une femme ayant un emploi sachant
qu’elle n'est pas considérée comme obèse.
1745 / 2400 =0,727.
c. En
considérant les résultats précédents, que peut-on dire de l’influence
de la corpulence sur le taux d’emploi des femmes en 2006 ?
Les femmes obèses ont plus de difficultés à trouver un emploi.
Partie B
Dans cette partie, on choisit un questionnaire au hasard parmi ceux des
hommes interrogés.
On reprend les mêmes notations pour les événements que dans la partie
A, c’est-à-dire :
E désigne l’événement : « le questionnaire choisi correspond à une
personne ayant un
emploi ».
O désigne l’événement : « le questionnaire choisi correspond à une
personne considérée
comme obèse ».
On admet que les probabilités associées à cette expérience aléatoire
sont représentées à l’aide
de l’arbre de probabilité suivant :
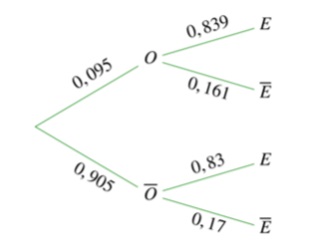 1.
1. Par lecture de
l’arbre, donner la probabilité qu’un homme ait un emploi sachant qu’il
est
considéré comme non obèse.
0,83.
2. Le rapport
d’étude conclut qu’il n’y a pas d’influence de la corpulence sur le
taux d’emploi des hommes en 2006. Comment peut-on le justifier à l’aide
de l’arbre précédent ?
Probabilité
qu’un homme ait un emploi sachant qu’il est considéré comme obèse :0,839.
0,83 est très peu différent de 0,839.