Mathématiques,
fonctions
Bac St2S 2014.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Métropole.
Au
début d’un effort physique, la consommation de glucose étant supérieure
à l’apport d’oxygène, l’organisme produit du lactate (aussi appelé
acide lactique) responsable, entre autres, de crampes musculaires.
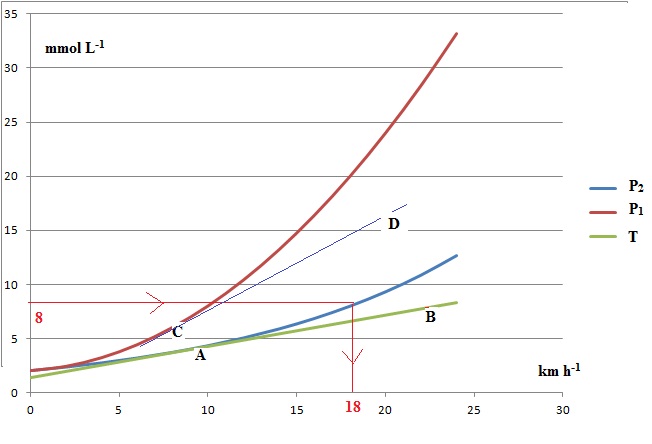
Dans l’annexe sont représentées les évolutions de la lactatémie,
c’est-à-dire la concentration en lactate, en millimoles par litre
(mmol.L−1), en fonction de la vitesse de course, exprimée en
kilomètres par heure (km.h−1), pour deux individus.
Le premier individu, P1, peu entraîné, voit sa lactatémie
augmenter rapidement tandis que celle du second individu, P2,
coureur de demi-fond, augmente moins rapidement.
La tangente à la courbe de lactatémie de P2 au point A de
coordonnées (9 ; 4) est représentée en vert. Cette droite passe par le
point B de coordonnées (22 ; 8).
Partie A.
Dans cette partie, on s’intéresse à la courbe représentant la
lactatémie du coureur P2.
On suppose que cette lactatémie est modélisée par une fonction f
définie sur l’intervalle [0 ; 20].
1. En s’aidant du graphique, et en
faisant apparaître les traits de construction utiles, déterminer
avec la précision que permet la lecture graphique :
a. la vitesse à
partir de laquelle la lactatémie dépasse 8 millimoles par litre ; 18 km
/h ;
b. la lactatémie du
coureur P2, s’il court à une vitesse de 9 kilomètres par
heure. 4 mmol / L
2. Déterminer, par
un calcul, f ′(9), le nombre dérivé de la fonction f en 9.
f '(9) est le coefficient directeur de la tangente T passant par les
points A et B.
f '(9) = (yB-yA) / (xB-xA)
=(8-4) /(22-9) =4 / 13.
3. On admet que la
fonction f est définie par :
f (x) = 2×1,08x pour tout nombre réel x appartenant à
l’intervalle [0 ; 20].
a. Déterminer une
inéquation qui permet de répondre, par le calcul, à la question 1 a.
b. Résoudre cette
inéquation dans l’intervalle [0 ; 20].
2×1,08x > 8 ; 1,08x > 4 ; x log 1,08 >
log 4 ; x > log 4 / log 1,08 ; x > 18 km /h.
Partie B.
On s’intéresse à la courbe représentant la lactatémie du coureur P1.
On admet que cette courbe est la représentation graphique de la
fonction g définie sur l’intervalle [0 ; 20] par g (x) = 0,05x2
+0,1x +2.
1. La fonction g ′
est la fonction dérivée de la fonction g . Déterminer g ′(x) pour tout
réel x appartenant à l’intervalle [0 ; 20].
g'(x) = 0,1 x+0,1.
2. Déterminer g
′(8) et construire la tangente à la courbe représentant la fonction g
au point d’abscisse 8. Justifier la construction.
g'(8)=0,8+0,1 = 0,9 ; g(8) = 0,05 x64 +0,8+2 =6.
La tangente passe par le point C( 8 ; 6).
Equation de la tangente y = 0,9 x +b ; 6 = 0,9 x8 +b ; b = -1,2.
La tangente passe également par le point D ( 20 ; 16,8).
QCM.
1. La fonction g
est définie sur l’intervalle [0 ; 100] par : g (x) = 4×0,7x+1
. On a alors :
a. g (2) = 2,96 ; b. g (2) = 21,952 ; c. g (2) = 1,372 vrai ; d. g (2)= 8,84.
g(2) = 4 x0,73 = 1,372.
2. La fonction h
est définie sur l’intervalle [0 ; 5] par : h(x) = x3 −6x2
−15x +3. La fonction h est dérivable sur l’intervalle [0 ; 5] et on
note h′ sa fonction dérivée. On a :
a. h′(x) = (3x
+3)(x −5) vrai ; b. h′(x) = 3x2 −6x +3 ; c. h′(x) = 3x2 −12x +3 ; d. h′(x) = −15x −15.
h'(x) = 3x2 -12x-15 =3 (x+1)( x-5).
3. La fonction m est définie sur [1
; 9]. On suppose que m est dérivable sur l’intervalle [1 ; 9] et on
note m′ sa fonction dérivée avec :
m′(x) = −2x +6 . On en déduit que :
a. La fonction m
est décroissante sur [1 ; 9] ; b.
La fonction m est croissante sur [1 ; 9]
c. La fonction m
est décroissante sur [1 ; 3] ; d.
La fonction m est croissante sur [1 ; 3], vrai.
m'(x) est positive sur [1 ; 3 [ : m(x) est strictement croissante
sur cet intervalle.
m'(x) est négative sur ]3 ; 9 ] :
m(x) est strictement décroissante sur cet intervalle.
m'(x) = 0 pour x = 3 ; m(x) présente un maximum pour x = 3.
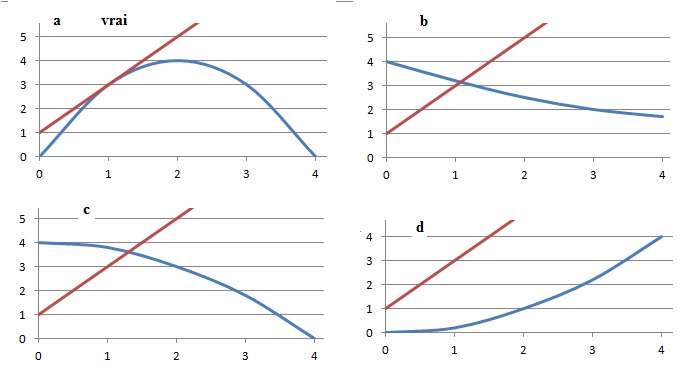
4. On donne les représentations
graphiques de 4 fonctions définies sur l’intervalle [0 ; 4] . On
suppose que chacune de ces fonctions est dérivable sur l’intervalle [0
; 4] . Laquelle admet la droite d’équation y = 2x +1 comme tangente en
un point de sa courbe représentative ?
|
|
|
Métropole septembre
Partie A
On arrondira au dixième les valeurs calculées dans cette partie.
Soit f la fonction définie sur l’intervalle [0 ; 12] par f (x) = 8×1,1x
.
1. On admettra que
la fonction f a le même sens de variation que la fonction g définie sur
l’intervalle
[0 ; 12] par g (x) = 1,1x .
Déterminer, en justifiant, le sens de variation de la fonction g sur
l’intervalle [0 ; 12] puis donner le tableau de variation de la
fonction f sur ce même intervalle.
Pour a positif, supérieur à 1, la fonction ax est croissante
sur R. Donc g(x) = 1,1 x est croissante sur R.
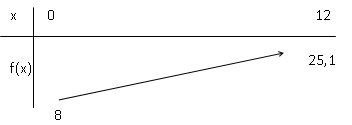
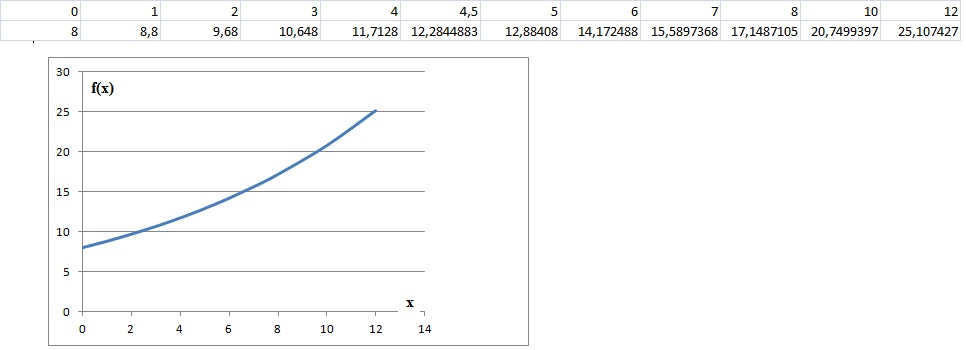
2. Compléter le
tableau de valeurs suivant :
3. Tracer la représentation
graphique correspondante.
Partie B.
Durant l’année 2013, un particulier faisait 8 heures de sport chaque
mois. À partir de janvier 2014, il décide d’augmenter de 10% chaque
mois son temps de pratique sportive mensuel.
1. Calculer son
nouveau temps de pratique sportive pour le mois de janvier 2014,
exprimé en heures et en minutes.
8 x1,1 = 8,8 h ou 8 h 48 min.
2. On désigne par
l’entier naturel n le rang dumois et par un le temps de
pratique sportive, en heures, du mois de rang n.
Ainsi u0 est égal à 8 et u1 désigne le temps de
pratique sportive pour le mois de janvier 2014.
Expliquer pourquoi un = 8×1,1n .
Chaque élément est obtenu en multipliant
le précédent par 1,1. La
suite est géométrique de raison q = 1,1 et de premier terme u0=8.
3.
Quel sera le temps de pratique sportive mensuel du particulier en
décembre 2014 ? On arrondira le résultat à l’heure.
n = 12 ; u12 = 8 x1,112 ~25 h.
4. Après
consultation de son médecin, il lui est conseillé de ne pas dépasser 16
heures mensuelles de pratique sportive. À partir de quel mois,
dépassera-t-il cette limite ? Détailler la méthode utilisée.
8×1,1n
<16 ; log 8 + n log 1,1 <log 16 ; 0,903 +0,0414 n < 1,204 ;
0,0414 n <0,301 ; n < 0,301 / 0,0414 ; n < 7,3.
On retient n = 7 ( fin juillet 2014).
|
|
|
|
Antilles septembre.
Un laboratoire de recherches médicales observe « in vitro » la
multiplication, par mitose accélérée, d’une cellule cancéreuse.
Les chercheurs veulent étudier l’effet du rayonnement d’ondes
millimétriques sur les cellules cancéreuses.
Après une période de multiplication des cellules, on note t = 0,
l’instant à partir duquel commence l’exposition au rayonnement d’ondes
millimétriques. La courbe ci-dessous est la représentation graphique du
nombre de cellules cancéreuses depuis le début du rayonnement.
Partie A : Étude graphique.
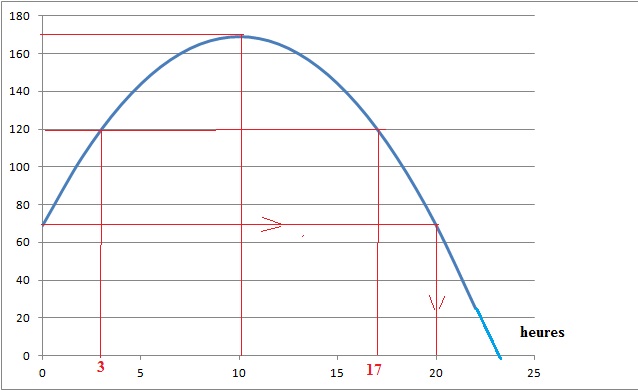
1. Déterminer le
nombre de cellules cancéreuses au début du rayonnement. 69.
2. Déterminer la
durée, approximative, d’exposition au rayonnement pour que le nombre de
cellules cancéreuses redevienne celui qu’il était au début de
l’exposition. 20 heures.
3. a. Après quelle
durée d’exposition le nombre de cellules cancéreuses est-il maximum ?
10 h.
b. Quelle est alors
la valeur de ce maximum ? 169.
4. Déterminer
pendant quelle durée d’exposition le nombre de cellules cancéreuses est
supérieur ou égal à 120.
Entre 3 h et 17 h soit durant 14 h.
5. Déterminer la
durée d’exposition nécessaire pour détruire toutes les cellules
cancéreuses 23 h.
Partie B. Étude théorique
Après observation, les chercheurs conviennent de modéliser l’évolution
du nombre de cellules cancéreuses exposées
à ce rayonnement par la fonction f définie sur l’intervalle [0 ; 23]
par f (t ) = −t 2 +20t +69
où t est la durée d’exposition et f (t ) le nombre de cellules
cancéreuses après t heures d’exposition à ce rayonnement.
1. Calculer f (15)
et interpréter le résultat par une phrase dans le contexte de
l’exercice.
f(15) = -152 + 20 x15 + 69 = 144.
Au bout de 15 h d'exposition, le nombre de cellules est égal à 144.
2. Calculer f '(t )
pour t appartenant à l’intervalle [0 ; 23], où f ' est la fonction
dérivée de la fonction f .
f '(t) = -2t +20= 2(10-t).
3. Étudier le
signe de f '(t ) sur l’intervalle [0 ; 23].
Si t appartient à [0 ; 10 [, f '(t) est positive et f(t) est
strictement croissante.
Si t appartient à ]10 ; 23 ], f '(t) est négative et f(t) est
strictement décroissante.
Si t = 10, f '(t)= 0, f présente un maximum.
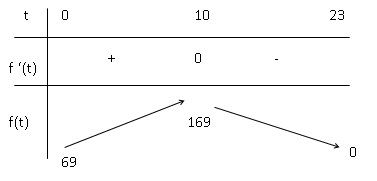
4. Construire le
tableau de variations de la fonction f sur l’intervalle [0 ; 23].
5. En utilisant la
question précédente, retrouver les résultats des questions 3. a. et 3.
b. de la partie A.
f(10) =-102+20x10+69=169.
|
|
Nlle Calédonie.
La
scintigraphie est une technique d’exploration du corps humain qui
permet de diagnostiquer des maladies. Lors d’une scintigraphie de la
glande thyroïde, on injecte
une dose d’iode dans le corps d’un patient. Cette dose se fixe sur la
glande thyroïde de ce patient puis se désintègre au cours du temps.
Le graphique donné représente le nombre de noyaux d’iode, exprimé
en milliards, restant fixés sur la glande thyroïde en fonction du temps.
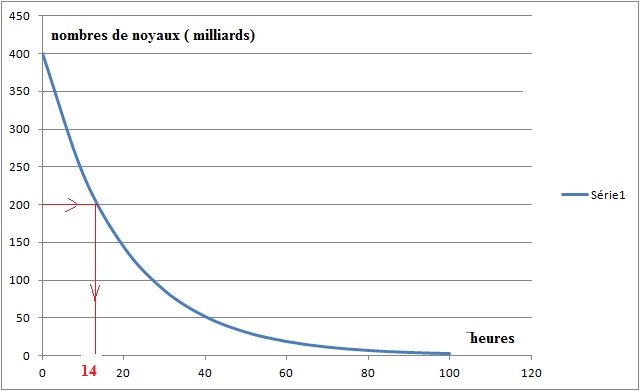
1. En utilisant le graphique, indiquer :
a. Le nombre de
noyaux injectés initialement. 400 milliards.
b. Le nombre
minimal d’heures à attendre pour que la moitié des noyaux injectés ait
été désintégrée. 14 heures.
On considère la fonction N définie sur l’intervalle [0 ; 100] par :N(t
)= 400×0,95t .
La courbe donnée est la représentation graphique de la fonction N
dans un repère orthogonal.
Pour tout temps t , exprimé en heures, on admet que N(t ) représente le
nombre de noyaux, exprimé en milliards, restant fixés sur la glande
thyroïde au temps t .
2. On admet que la
fonction N a le même sens de variation que la fonction f ,fonction
exponentielle de base 0,95 définie sur [0 ; 100] par f (t ) = 0,95t
.
Justifier que la fonction N est décroissante sur [0 ; 100].
Pour a
positif,appartenant à l'intervalle ]0 ; 1 [, la fonction ax
est décroissante sur R. Donc f(t) = 0,95 t est décroissante
sur R.
3.
a. Résoudre l’inéquation : N(t )< 40.
400×0,95t<
40 ; 10 x 0,95 t <1 ; log 10 + t log 0,95 < log
1 ;
1-0,0227 t <0 ; 0,0227 t > 1 ; t > 1 /0,0227 ; t > 44,9
heures.
Solutions de l'inéquation : ]44,9 ; 100 ]
b.
On considère que le produit injecté a été éliminé de l’organisme
lorsqu’il reste moins de 10% de la quantité injectée initialement.
Déterminer
au bout de combien de temps on peut considérer que le produit a été
éliminé de l’organisme. On exprimera cette quantité en jours et
en heures, arrondie à l’heure.
44,9 h = 24 +20,9 ~ 1 jour et 21 h.
4. Calculer le
pourcentage de diminution du nombre de noyaux entre la première heure
et la sixième heure. Arrondir à 0,1%.
N(1 )= 400×0,95=380 ; :N(6 )= 400×0,956 =294 ; (294-380) /
380 x100 = -22,6 %.
|
|