Mathématiques,
QCM, pourcentages, suites numériques
Bac St2S 2013.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie.
Une
élève de première ST2S, a choisi comme thème, pour son dossier
d’activités interdisciplinaires, le saturnisme chez les enfants en
France. Le saturnisme est une maladie qui correspond à une intoxication
aiguë ou chronique par le plomb.
Suite à ses recherches, elle a trouvé des statistiques indiquant le
nombre d’enfants de 0 à 6 ans ayant un taux de plomb dans le sang
anormalement élevé sur la période 2005 – 2009 en France. Ce nombre est
appelé nombre de plombémies.
Le tableau suivant est extrait d’une feuille de tableur que l’élève a
produite. La colonne C est au format Pourcentage.
|
A
|
B
|
C |
1
|
Anné
du prélévement sanguin
|
Nombre
de plombémie
|
Taux
d'évolution entre 2 années consécutives
|
2
|
2005
|
9029
|
|
3
|
2006
|
7871
|
|
4
|
2007
|
7470
|
|
5
|
2008
|
7393
|
|
6
|
2009
|
6559
|
|
Source : Système national de
surveillance des plombémies de l’enfant
Partie A
1. Quelle formule doit-on rentrer dans la cellule C3 qui,
recopiée vers le bas, donne le taux d’évolution
du nombre de plombémies entre deux années consécutives ?
=(B2-B3)/B2
2. Calculer le taux
d’évolution entre l’année 2008 et l’année 2009.
On donnera le résultat en pourcentage arrondi à 0,1% près.
(7393-6559) / 7393 x100 ~11,3 %.
3. Calculer le
nombre total S de plombémies dénombrées entre 2005 à 2009, les années
2005 et 2009 étant incluses.
9029 +7871 +7470 +7393 +6559=38 322.
Partie B.
L’élève souhaite estimer le nombre de plombémies pour l’année 2010.
Pour cela, elle considère que le nombre de plombémies baisse de 11% par
année à partir de 2005.
Elle modélise alors cette évolution par une suite géométrique de terme
général un où n désigne un entier naturel et un
représente le nombre de plombémies de l’année (2005 + n).
On a alors u0 = 9029.
1. a. Montrer que
la raison de cette suite est égale à 0,89.
Chaque année la plombémie baisse de 11%, d'où la raison de la suite
géométrique ou coefficient multiplicateur : 1-0,11 = 0,89.
b. Calculer u1.
On arrondira à l’unité.
0,89 xu0 = 0,89 x9029 = 8
036.
2. a. Exprimer un
en fonction de n.
un = 0,89n u0=0,89n x9029.
b. Calculer alors
le nombre de plombémies que l’élève peut estimer pour l’année 2010. On
arrondira le résultat à l’unité.
n = 5 ; u5 = 9029 x0,895 ~5042.
3. On rappelle le
résultat suivant :
Si (un) est une suite géométrique de premier terme u0
et de raison q avec q différent
de 1, alors :
u0 +u1 +u2 +· · ·+un = u0
×(1−qn+1) / (1−q).
a. Calculer, pour
les années 2005 à 2009 incluses, le nombre total T de plombémies que
l’élève
peut obtenir avec sa modélisation. On arrondira le résultat à l’unité.
T = 9029x(1-0,895)/(1-0,89)=36
247.
b. L’élève
considère que sa modélisation est acceptable si l’écart entre T et S
n’excède pas 7%
de S. (On rappelle que S est défini dans la question 3 de la partie A).
Sa modélisation est-elle acceptable ? Justifier.
(T-S) / S x100 = (36247-38322) /38322 x100 = -5,4 %, valeur inférieure
à 7%. La modèlisation est correcte.
|
|
|
Antilles
Partie A.
Dans cette partie, les résultats seront exprimés en pourcentage et
arrondis à 0,1% près.
1. En France, les 4
premiers groupes iso-ressources (GIR 1 à 4) de la grille nationale
AGGIR ouvrent droit à l’allocation personnalisée d’autonomie (APA).
Fin 2010, 1 200 milliers de personnes âgées dépendantes ont bénéficié
de l’APA dont 734 milliers ont directement perçu l’APA à domicile.
Voici le tableau donnant, en milliers de personnes, le nombre de
bénéficiaires de l’APA selon le degré de dépendance de la personne :
|
à
domicile
|
en
établissements
|
Total
|
GIR1
|
19
|
86
|
105
|
GIR2
|
131
|
191
|
322
|
GIR3
|
159
|
79
|
238
|
GIR4
|
425
|
110
|
535
|
Ensemble
|
734
|
466
|
1200
|
Source
: Drees, enquête trimestrielle auprès des conseils généraux
a. Quelle
est, en pourcentage, la proportion des bénéficiaires de l’APA qui ont
perçu cette allocation directement à domicile ? Arrondir le résultat à
0,1% près.
734 / 1200 x100 ~ 61,2 %.
b. Parmi les
personnes bénéficiant de l’APA en établissement, quelle est, en
pourcentage, la proportion de celles relevant du GIR2 ? On arrondira le
résultat à 0,1% près.
191 / 466 x100 ~41 %.
2. En 2009, 718
milliers de personnes ont bénéficié de l’APA à domicile. Calculer le
taux d’évolution du nombre de bénéficiaires de l’APA à domicile entre
2009 et 2010. On exprimera ce taux en pourcentage, arrondi à 0,1% près.
(734-718) / 734 x100 ~2,2 %.
Partie B.
On note u0 le nombre de milliers de personnes bénéficiant de
l’APA à domicile à la fin de l’année 2010, et un le nombre de milliers
de personnes bénéficiant de l’APA à domicile à la fin de l’année
(2010+n). Ainsi, u0 = 734. On admet que le nombre de
bénéficiaires de l’APA à domicile augmente de 2,2% chaque année à
partir de 2010.
On utilise un tableur pour calculer des termes de la suite (un)
:
|
A
|
B
|
C
|
D
|
1
|
Année
|
n
|
un
|
|
2
|
2010
|
0
|
734
|
|
3
|
2011
|
1
|
|
|
4
|
2012
|
2
|
|
|
5
|
2013
|
3
|
|
|
1.
Calculer u1. Donner une valeur approchée à l’unité près.
734 x(1,022)=750.
2. Quelle est la
nature de la suite (un) ? Préciser sa raison.
On passe d'un terme au suivant, en multipliant ce terme par 1,022 : il
s'agit d'une suite géométrique de raison q = 1,022.
3. Quatre formules
à saisir dans la cellule C3, puis à recopier vers le bas pour afficher
les valeurs de un, sont proposées :
= 734⋆1,022 ; =C2⋆1,022
; C$2⋆1,022 ; =$C$2⋆1,022.
Une seule est exacte. Indiquer cette formule sur votre copie.
4. Exprimer un
en fonction de n, pour tout entier naturel n.
un
=734 x 1,022n.
5. Quel nombre de
personnes bénéficiant de l’APA à domicile peut-on prévoir pour la fin
de l’année 2020 ? Donner la réponse au millier de personnes près.
n = 10 ; u10 =734 x1,02210~912.
6. Si la
progression reste la même, à partir de la fin de quelle année le nombre
de personnes bénéficiant de l’APA à domicile dépassera-t-il un million ?
734 x1,022n = 1000 ; 1,022n
=1000 / 734 ;
n log (1,022)= log (1000 / 734) ; n =[ log (1000 / 734) ]
/log (1,022) = 14,2. ( fin 2024).
|
|
|
|
Métropole.
L’évolution de l’endettement d’une entreprise est donnée par le tableau
ci-dessous, extrait d’une feuille de calcul.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
1
|
Année
|
2011
|
2012
|
2013
|
2014
|
2015
|
2016
|
2
|
Endettement
( miliers € ) |
400
|
410
|
|
|
|
|
3
|
Pourcentage
d'évolution entre deux années consécutives
|
|
|
|
|
|
|
1. Le pourcentage
d’augmentation de l’endettement de l’entreprise entre les années 2011
et 2012 est :
a. 0,25% ; b. 2,5% ; c. 10,25% ; d. 0,025%.
(410-400) / 400 x100 = 2,5 %.
À partir de l’année 2012, on admet que l’endettement de l’entreprise
diminuera chaque année de 5%.
2. La formule à
saisir dans la cellule D2, qui recopiée vers la droite, permettra
d’afficher les valeurs en milliers d’euros de l’endettement de
l’entreprise pendant les années qui suivent 2012 est :
a. =410*0,95 ; b. =C2*0,05 ; c. =C2*0,95 ; d. =$C$2*0,95.
=C2*0,95.
3. On désigne par n
un entier naturel. On note un l’endettement de l’année 2012
+ n, ainsi u0 = 410. L’endettement de l’entreprise en
milliers d’euros
pendant l’année 2020 est :
u8 = 410×0,958 ; b. u8
= 410×0,959 ; c. u9 = 410×0,958
; d. u9 = 410×0,959.
4. On cherche à
partir de quelle année l’endettement de l’entreprise aura diminué de
moitié.
Pour cela l’inéquation à résoudre s’écrit 410×0,95n < 205, où n désigne un
entier naturel. Les solutions de cette inéquation sont les entiers
n tels que :
0,95n <
205 /410 ; 0,95n <
0,5 ; n log (0,95) <
log (0,5) ;
log (0,95) et log (0,5) sont négatifs ; n > log (0,5) / log (0,95).
5. Dans le tableau
les cellules C3 à G3 sont en pourcentages. La formule à saisir dans la
cellule C3, qui recopiée vers la droite, permet d’afficher le
pourcentage d’évolution de l’endettement de l’entreprise entre deux
années consécutives est :
a. =($C2-$B2)/$B2 ; b. =C2-B2/B2 ; c. =C2/B2 ; d. =(C2-B2)/B2.
|
|
Polynésie septembre.
Partie A.
Le tableau suivant est une feuille de tableur qui donne par région la
puissance produite (en MW) par des éoliennes dans 15 régions de France
entre le 1er janvier et le 1er octobre 2010. On souhaite renseigner la
colonne C et indiquer la part de la puissance produite dans chaque
région par rapport à la puissance totale durant la période observée.
Les cellules de la colonne C sont au format pourcentage.
|
A
|
B
|
C
|
1
|
Région
|
Puissance
(MW)
|
Part
de puissance (%)
|
2
|
Champagne
|
256
|
|
3
|
Centre
|
82
|
|
4
|
Pays
de Loire
|
60
|
|
5
|
Hte
Normandie |
51,2
|
|
6
|
Midi
Pyrénées
|
44
|
|
7
|
Picardie
|
39,1
|
|
8
|
Bretagne
|
36,8
|
|
9
|
Auvergne
|
16
|
|
10
|
Basse
Normandie
|
16
|
|
11
|
Bourgogne
|
12
|
|
12
|
Lorraine
|
12
|
|
13
|
Poitou
|
8
|
|
14
|
Rhône
Alpes
|
4,6
|
|
15
|
Languedoc
|
3,7
|
|
16
|
Guadeloupe
|
1,38
|
|
17
|
Total
|
642,78
|
|
Source : Syndicat des énergies
renouvelables - France Énergie Éolienne
1. Quelle est la
part en pourcentage de la puissance produite en région Basse Normandie
par rapport à la puissance totale produite ? On donnera le résultat
arrondi au centième.
16 / 642,78 x100 = 2,49 %.
2. Quelle formule
faudrait-il entrer dans la cellule C2 pour obtenir par recopie vers le
bas, les parts en pourcentage de la puissance produite par chaque
région par rapport à la puissance totale ?
=B2 /$B$17.
Partie B.
En France, à la fin de l’année 2005, on comptait 940 éoliennes. Depuis,
chaque année, 500 éoliennes supplémentaires ont été installées. On
note, pour tout entier naturel
n, un le nombre d’éoliennes présentes en France à la fin de
l’année (2005+n).
On a donc u0 = 940.
1. Déterminer la
nature de la suite (un). On précisera sa raison.
(940 +500) / 940 = 1,532.
Chaque année, le nombre total d'éoliennes est égal au nombre
d'éoliennes en service l'année précédente augmenté de 500.
un est une suite arithmétique de raison r = 500.
2. Exprimer un
en fonction de n.
un = u0 + 500 xn = 940 +1500 xn
3. Combien
d’éoliennes y aura-t-il en France à la fin de l’année 2013 ?
n = 8 ; u8 = 940 +500 x8 =4940.
Métropole septembre.
Partie A.
Le service de l’eau d’une ville a été privatisé en 1990, puis géré par
la commune à partir de 1996. Le tableau ci-dessous, extrait d’une
feuille de calcul, donne l’évolution du prix de
l’eau de cette ville, en euros pour 120 m3, entre les années
1990 et 1996.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
1
|
Année
|
1990
|
1991
|
1992
|
1993
|
1994
|
1995
|
1996
|
2
|
Prix
de 120 m3 d'eau
|
185
|
177
|
189
|
208
|
216
|
222
|
228
|
3
|
Taux
d'évolution entre deux années consécutives ( %)
|
|
|
|
|
|
|
|
1.
Calculer le taux d’évolution du prix de 120 m3
d’eau entre 1990 et 1991. On donnera le résultat sous forme de
pourcentage arrondi à 0,1%.
(177-185) / 185 x 100 ~ - 4,3 %.
2. Quelle formule
doit-on rentrer dans la cellule D3, qui recopiée vers la droite, donne
le pourcentage d’évolution du prix de 120 m3 d’eau entre
deux années consécutives ?
(On admet que les cellules C3 à H3 sont en pourcentage).
=(D2-C2)/C2.
On admet que, si le service de l’eau était resté privatisé, le prix de
120 m 3 aurait augmenté de 2,5% par an à partir de l’année
1996.
On note alors un le prix de 120 m3 d’eau pour
l’année (1996+n) où n est un entier naturel. On a alors u0 =
228.
3. Justifier que la
suite (un) est une suite géométrique dont on précisera la
raison.
Pour passer d'un terme au suivant on multiplie le terme par un
coefficient multiplicateur égal à :1,025. Un est une
suite géométrique de raison q = 1,025.
4. Exprimer un en
fonction de n.
un = u0 qn = 228 x 1,025n.
5. Quel aurait été
le prix de 120 m3 d’eau en 2012 si le service était resté
privatisé ? (Le résultat sera arrondi à l’unité).
n = 16 ; u16 = 228 x 1,02516 ~338 €.
6. À partir de
quelle année, le prix de 120 m3 d’eau aurait-il dépassé 300 € ?
228 x 1,025n>300
; 1,025n>300 /228 ; n
log (1,025) > log(300 / 228) ; n > log(300/228) / log (1,025)
; n >11,11.
Durant l'année 1996 +12 = 2008.
Partie B.
La ville gère le service de l’eau depuis 1996. Le tableau ci-dessous
donne l’évolution du prix de 120 m3 d’eau depuis 1998.
Année
|
1998
|
2000
|
2002
|
2004
|
2006
|
2008
|
2010
|
2012
|
Rang
de l'année xi
|
0
|
2
|
4
|
6
|
8
|
10
|
12
|
14
|
Prix
de 120 m3 d'eau yi
|
191
|
202
|
198
|
202
|
204
|
208
|
215
|
220
|
1. Représenter
le nuage de points de coordonnées ( xi ; yi )
dans un repère orthogonal.
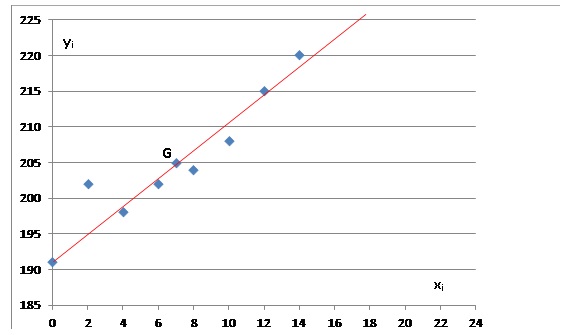
2. Déterminer les
coordonnées du point moyen G de ce nuage de points. Placer le point
moyen G dans le repère.
xG=(2+4+6+8+10+12+14) / 8 =7.
yG=(191 +202
+198 +202 +204 +208 +215 +220) / 8 = 205.
3.
On admet que la droite (D) d’équation y = 1,8x+192,4 réalise un
ajustement affine du nuage de points. Cet ajustement est fiable
jusqu’en 2020.
a. Vérifier que le
point moyen G appartient à la droite (D).
y = 1,8 x 7 +192,4 =205 = yG.
b. Tracer la droite
(D) dans le repère précédent.
c. En tenant
compte de cet ajustement affine, déterminer le prix de 120 m3
d’eau que l’on peut prévoir pour l’année 2020.
x = 22 ; y = 1,8 x22 +192,4 = 232 €.
Antilles septembre.
Le tableau suivant, extrait d’une feuille d’un tableur, donne le nombre
d’équipements IRM (Imagerie par RésonanceMagnétique) à usage humain
installés en France
métropolitaine depuis 2003.:
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
1
|
Année
|
2003
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2
|
Rang
de l'année xi
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
3
|
Nombre
d'IRM, yi
|
230
|
281
|
352
|
393
|
419
|
463
|
495
|
543
|
4
|
Taux
d'évolution par rapport à l'année précédente ( %)
|
|
|
|
|
|
|
|
|
Partie A :
1. Calculer le taux
d’évolution du nombre d’équipements IRM en France de 2003 à 2004.
On exprimera ce taux en pourcentage, arrondi à 1% près.
(281 -230) / 230 x 100 = 22,17 ~22 %.
2. La ligne 4 est
au format pourcentage.
Quelle formule peut-on saisir dans la cellule C4 et recopier vers la
droite pour compléter la ligne 4 ?
=(C3-B3)/B3.
Partie B :
1. a. Représenter
le nuage de points de coordonnées (xi ; yi )
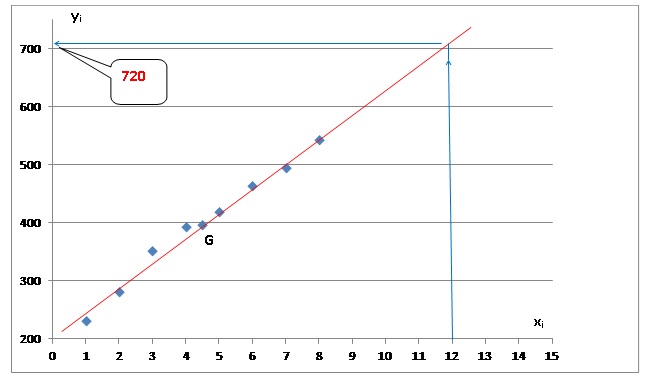
b. Calculer les
coordonnées du point G, point moyen du nuage de points. Placer le point
G sur le graphique précédent.
xG=(1+2+3+4+5+6+7+8)
/ 8 =4,5.
yG=(230 +281
+352 +393 +419 +463 +495 +543) / 8 = 397.
2.
On admet que la droite (D) d’équation y = 43x +203,5 constitue une
droite d’ajustement convenable du nuage.
a. Vérifier que le
point G appartient à la droite (D).
y = 43 x4,5 +203,5 =397 = yG.
b. Tracer la droite
(D) sur le graphique précédent en indiquant les points utilisés.
Le point G et le point de coordonnées (10 ; 633,5 ).
c. À l’aide du
graphique, estimer le nombre d’équipements IRM en France au 1er janvier
2014. 720.
d. Estimer, par le
calcul et l’ajustement proposé, à partir de quelle année le nombre
d’équipements IRMen France dépasserait, selon cet ajustement 750.
43x +203,5 >750 ; 43x
> 750-203,5 : 43x >546,5 ; x > 546,5 / 43 ; x >12,7 (13),
durant l'année 2015 ).
Nlle Calédonie.
Le tableau ci-dessous, extrait d’une feuille de tableur, donne
l’évolution, depuis 2004, du nombre
de pactes civils de solidarité (PACS) conclus en France jusqu’en 2010.
La ligne 4 est au format pourcentage.
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
1
|
Année
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2
|
Rang
de l'année xi
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
3
|
Nombre
de milliers de PACS, yi
|
40,1
|
60,5
|
77,3
|
102
|
146
|
174,5
|
205,6
|
4
|
Taux
d'évolution par rapport à l'année précédente ( %)
|
|
|
|
|
|
|
|
Champ
: France (non compris Saint-Martin et Saint-Barthélemy). Sources :
Institut national de la statistique et des études économiques.
Il n’est pas demandé de compléter le tableau.
1. Calculer le taux
d’évolution en pourcentage, arrondi à 0,01%, du nombre de PACS entre
les années 2004 et 2005.
(60,5-40,1) / 40,1 x100 =0,5087 ~0,51.
2. Quelle formule
doit-on saisir en C4 pour vérifier ce résultat et pour obtenir les
autres taux d’évolution en faisant une copie vers la droite ?
=(C3-B3) /C3.
3. Représenter le
nuage de points de coordonnées (xi ; yi ), dans
un repère orthogonal.
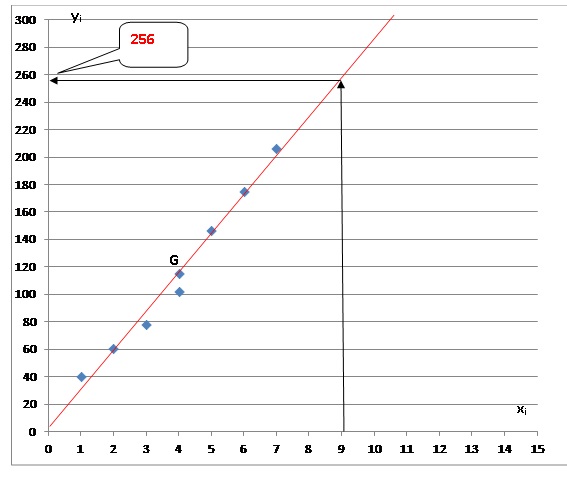
b. Déterminer les
coordonnées du point moyen G de ce nuage de points et placer ce point
dans le repère précédent. On arrondira chaque coordonnée au centième.
xG =(1+2+3+4+5+6+7)/7=4 ;
yG =(40,1 +60,5 +77,3 +102 +146 +174,5 +205,6) / 7 =115,14.
4. a. On suppose
que la droite (D) d’équation y = 28,3x +1,8 réalise jusqu’en 2015 un
ajustement affine du nuage de points. Tracer la droite (D).
b. Déterminer
graphiquement une estimation du nombre de PACS en 2012. 256.
c. Déterminer, par
le calcul, l’année au cours de laquelle, le nombre de PACS devrait
dépasser 300 000.
28,3x +1,8 >
300 ; 28,3 x >300-1,8 ; 28,3 x >298,2 ; x > 298,2 / 28,3
; x >10,5. Au cours de l'année 2014
).
|
|