Mathématiques,
probabilités
Bac St2S 2013.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Polynésie.
Un
test contre une maladie animale a été élaboré par une entreprise
pharmaceutique. Pour connaître sa fiabilité, une population comportant
des animaux malades et des animaux sains est testée.
On sait que la proportion d’animaux malades dans la population testée
est de 75%;
parmi les animaux malades, 95% ont un test positif ;
parmi les animaux sains, 89% ont un test négatif.
On choisit au hasard un animal de la population testée. On note :
M l’événement : « l’animal est malade » ;
P l’événement : « le test est positif » ;
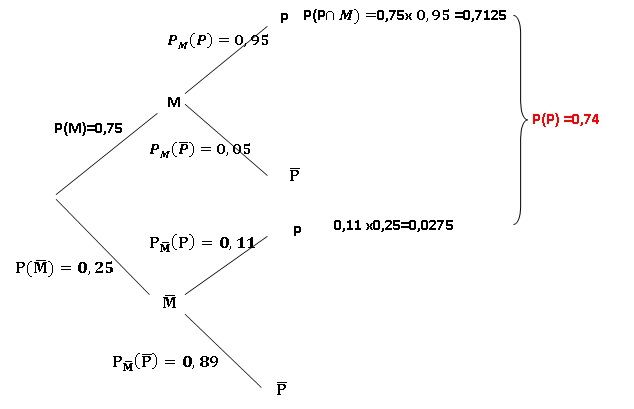
1. La probabilité que l’animal
choisi soit sain est égale à :
a. 0,25, vrai ; b. 0,11 ; c. 0,037 5
; d. 0,712 5.
2. La probabilité
que, parmi les animaux sains, le test soit positif est égale à :
a. 0,0275 ; b. 0,11, vrai ; c. 0,2225 ; d. 0,05.
3. La probabilité
de l’évènement "letest est négatif " sachant M est égale à :
a. 0,75 ; b. 0,05, vrai ; c. 0,0375 ; d. 0,94
4. La probabilité
de l’évènement P ∩M est égale à :
a. 0,95 ; b. 0,75 ; c. 0,7125, vrai ; d. 0,1045.
5. La probabilité
de l’évènement P est égale à :
a. 0,75 ; b. 0,95 ; c. 1,06 ; d. 0,74,
vrai.
|
|
|
Antilles
Le
tableau ci-dessous donne le nombre d’abonnements au service de
téléphonie mobile en France entre fin 2001 et fin 2009, exprimé en
millions. Source : Eurostat
Année
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
Rang
xi
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
Nombre
d'abonnements yi
|
37
|
38,6
|
41,7
|
44,5
|
48,1
|
51,7
|
55,3
|
58
|
61,5
|
On définit ainsi une série statistique (xi
; yi ) pour i allant de 1 à 9.
1. a. Représenter
le nuage de points de coordonnées (xi
; yi )
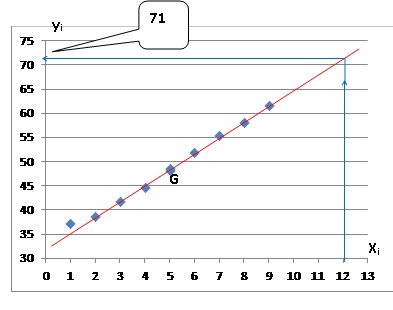
b. Expliquer pourquoi un ajustement
affine de ce nuage est envisageable.
Les points semblent alignés.
c. Calculer les
coordonnées, à 0,1 près, du point moyen G du nuage puis placer G sur le
graphique précédent.
xG=(1 +2 +3 +4 +5 +6 +7 +8 +9) / 9 =5.
yG=(37 +38,6 +41,7 +44,5 +48,1 +51,7 ++55,3 +58 +61,5) / 9 =
48,5.
Dans la suite de l’exercice, deux méthodes différentes de modélisation
seront utilisées.
2. Méthode graphique
a. Sans effectuer
de calcul, tracer une droite passant par le point G qui réalise un
ajustement affine du nuage de points.
b. Estimer, au
million d’abonnements près, à l’aide du graphique, le nombre
d’abonnements au service de téléphonie mobile en France fin 2012.
Méthode algébrique
On admet dans cette partie que la droite d’équation : y = 3,2x +32,5
réalise un bon ajustement de ce nuage.
a. Vérifier, par le
calcul, que cette droite passe par le point G.
y = 3,2 x5 +32,5 = 48,5 = yG.
b. Estimer, à
0,1million d’abonnements près, par le calcul, le nombre d’abonnements
au service de téléphonie mobile en France fin 2012.
y = 3,2 x12 +32,5 = 70,9.
c. Les dernières
données disponibles indiquent qu’il y a 70,4 millions d’abonnements au
service de téléphonie mobile en France en juin 2012. L’estimation
obtenue à la question b. vous parait-elle surestimer ou sous estimer la
réalité ?
L'estimation obtenue à la question b surestime d'environ 0,5 million le
nombre d'abonnements réels.
|
|
|
|
Métropole
Fin
2010, 1 200 000 personnes âgées dépendantes ont bénéficié de
l’Allocation Personnalisée d’Autonomie (APA), soit à domicile, soit en
établissement. Ces personnes sont classées dans quatre Groupes
Iso-Ressources (GIR) en fonction des différents stades de pertes
d’autonomie.
Les résultats, exprimés en milliers de personnes, d’une enquête
réalisée en 2010 auprès des conseils généraux ont permis de construire
le tableau
|
à
domicile
|
en
établissements
|
Total
|
GIR1
|
19
|
86
|
105
|
GIR2
|
131
|
191
|
322
|
GIR3
|
159
|
79
|
238
|
GIR4
|
425
|
110
|
535
|
Ensemble
|
734
|
466
|
1200
|
Source
: Drees, enquête trimestrielle auprès des conseils généraux
1. Justifier, par
un calcul approprié, chacune des informations suivantes dans lesquelles
les résultats ont été arrondis à l’unité.
a. Le pourcentage
des personnes de l’étude qui vivent à domicile est égal à 61%.
734 / 1200 x100 = 61 %.
b. 3% des personnes
de l’étude vivant à domicile sont classées en GIR1.
19 / 734 x100 =2,6 % ~3%.
Pour chacune des questions suivantes, on donnera les résultats sous
forme décimale, arrondie au centième.
2. On choisit au
hasard le dossier d’une personne agée dépendante bénéficiant de l’APA.
On considère les évènements suivants :
G : « Le dossier est celui d’une personne classée en GIR1 ».
E : « Le dossier est celui d’une personne vivant en établissement ».
a. Calculer la
probabilité des évènements G et E.
P(G) = 105 / 1200 =0,0875 ~ 0,09.
P(E) = 466 / 1200 =0,3883 ~0,39.
b. Définir par une
phrase chacun des évènements suivants G ∩E et G ∪E puis calculer leur
probabilité.
G ∩E : la personne est classée en GIR1 et vit en établissement.
P(G ∩E) = 86 / 1200 =0,0717 ~0,07.
G ∪E : a personne est classée en GIR1 ou vit en établissement.
P(G ∪E)=P(G) + P(E) -P(G ∩E) =0,0875 +0,3883 -0,0717 = 0,4041 ~0,41.
c. Sachant que le
dossier choisi est celui d’une personne classée en GIR4, calculer la
probabilité que cette personne vive à domicile.
425 / 535 =0,794 ~0,79.
d. Calculer PE
(G).
P(G ∩E) / (P(E) =0,0717 / 0,3883 =0,1846 ~0,18.
|
|
Polynésie septembre.
En
cas de menace d’accouchement prématuré, on peut effectuer sur les
femmes enceintes de 24 à 34 semaines d’aménorrhée un test de détection
de la fibronectine foetale. Ce test permet d’évaluer les risques d’un
accouchement dans les 14 jours et d’adapter la prise en charge de la
patiente.
Si le test est négatif, on peut envisager le retour à domicile de la
patiente et s’il est positif, l’orienter vers une maternité adaptée à
son état.
Dans une maternité, 23% des patientes testées ont eu un test positif.
Parmi celles-ci, 33%ont accouché dans les 14 jours après le test. Parmi
les patientes ayant eu un test
négatif, 98% n’ont pas accouché au cours des 14 jours suivant le test.
On choisit au hasard une patiente, parmi les patientes testées dans
cette maternité. On note :
T , l’évènement « le test de la patiente est positif » ;
A, l’évènement « la patiente a accouché dans les 14 jours qui suivent
le test ».
Dans les questions 1 à 5, les probabilités seront données sous forme
décimale exacte.
1. Donner les
probabilités suivantes :
p(T ), probabilité de l’évènement T. 0,23.
PT (A), probabilité de l’évènement A sachant T. 0,33.
2. Recopier et
compléter l’arbre pondéré suivant :
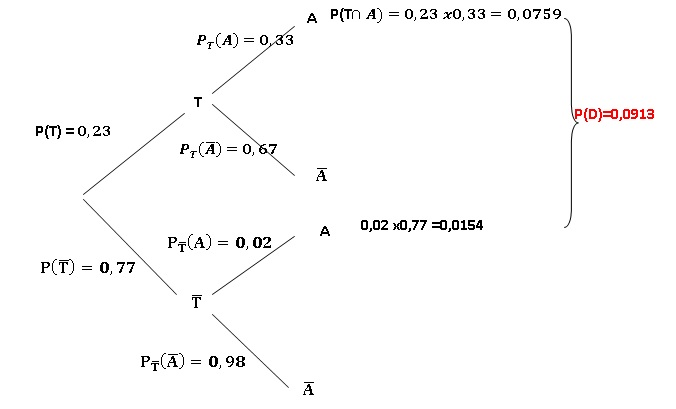
3. Calculer la probabilité que la
patiente ait un test négatif et accouche dans les 14 jours qui suivent
le test. 0,0154.
4. a. Calculer la
probabilité de l’évènement T ∩ A. 0,0759.
b. En déduire la
probabilité de l’évènement A.
0,0759 + 0,0154 = 0,0913.
c. La patiente
choisie a accouché dans les 14 jours qui suivent le test. Quelle est la
probabilité que son test ait été positif ? On arrondira le résultat au
centième.
P(T ∩ A) / P(A) =0,0759 / 0,0913 = 0,83.
Métropole septembre.
Une
enquête a été menée auprès de 1 700 habitants de diverses régions
françaises consommant de l’eau du robinet ou de l’eau en bouteille. Les
résultats de l’enquête
sont répartis par région dans le tableau ci-dessous :
|
Nombre
de personnes
consommant de l'eau du robinet
|
Nombre
de personnes
consommant de l'eau en bouteille |
Total
|
Nombre
de personnes
habitant en région pariisienne
|
557
|
274
|
831
|
Nombre
de personnes
habitant en région Nord
|
224
|
243
|
467
|
Nombre
de personnes
habitant en région Sud ouest
|
309
|
93
|
402
|
Total
|
1090
|
610
|
1700
|
On considère les évènements
suivants :
N : « La personne interrogée habite dans la région nord. »
R : « La personne interrogée consomme de l’eau du robinet. »
Pour chacune des questions suivantes, on donnera les résultats sous
forme décimale, arrondie au centième.
1. On choisit au
hasard une personne parmi toutes les personnes interrogées.
a. Calculer la
probabilité de l’évènement R.
1090 / 1700 =0,6412 ~ 0,64.
b. Calculer la
probabilité. de l'événement " la personne interrogée ne consomme pas
d'eau du robinet".
1-0,6412 ~0,36.
c. Définir par une
phrase l’évènement N ∩ R puis calculer sa probabilité.
La personne interrogée habite dans le Nord et consomme de l'eau du
robinet. Sa probabilité est : 224 / 1700 = 0,1318 ~0,13.
d. Définir par une
phrase l’évènement N ∪ R puis
calculer sa probabilité.
La personne interrogée habite dans le Nord ou consomme de l'eau du
robinet.
P(N ∪ R) = P(R) + P(N) -P(N ∩ R)=0,6412
+467 / 1700 -0,1318 = 0,7841 ~0,78.
2.
On veut comparer le type de consommation d’eau suivant les régions :
a. Déterminer la
probabilité qu’une personne interrogée consomme l’eau du robinet
sachant qu’elle habite la région nord.
PN(R) =P(N ∩ R) / P(N) =224 / 467 = 0,48.
b. Dans quelle
région faudrait-il se placer pour que la probabilité qu’une personne
interrogée consomme l’eau du robinet soit la plus élevée ?
En région parisienne 557 / 831 = 0,67 ; En région Sud ouest : 309 / 402 ~0,77.
Antilles septembre.
On donne les informations suivantes sur les infirmiers (hommes ou
femmes) exerçant en France, au 1er janvier 2010 :
• 516 000 infirmiers (hommes ou femmes) exercent en France.
• Ils sont répartis en trois catégories : les « infirmiers libéraux »
(hommes ou femmes), les « salariés hospitaliers » (hommes ou femmes) et
les « autres salariés ».
• 70% des infirmiers (hommes ou femmes) sont des « salariés
hospitaliers ».
• 77 200 sont « infirmiers libéraux » (hommes ou femmes) parmi eux, 80%
sont des femmes.
• 450 000 infirmiers sont des femmes ; parmi elles, 15% sont dans la
catégorie « autres salariés ».
1. Compléter le
tableau.
|
Hommes
|
Femmes
|
Total
|
Infirmiers
libéraux
|
77
200-61760=15 440
|
77200
x0,80=61 760
|
77
200
|
Salariers
hospitaliers
|
361
200 -320 740 =40 460
|
450
000 -61 760-67 500 =320 740
|
516
000 x 0,70 =361 200
|
Autres
salariès
|
77
600 -67 500 =10 100
|
450
000 x0,15 =67500
|
516
000-361 200-77200 =77 600
|
Total
|
516
000-450 000 =66 000
|
450
000
|
516
000
|
Dans les questions suivantes les résultats
seront arrondis à 10−2 près.
2. On choisit au
hasard une personne parmi les 516 000 infirmiers exerçant en France. On
considère les évènements suivants :
A : « La personne est une femme »,
B : « La personne est "infirmier libéral" ».
a. Calculer la
probabilité de chacun des évènements A et B.
P(A) = 450 000 / 516 000 = 0,8721 ~0,87.
P(B) =77 200 / 516 000 = 0,1496 ~0,15.
b. Exprimer
l’évènement A∩B à l’aide d’une phrase, puis calculer sa probabilité.
L'infirmier libéral est une femme; sa probabilité est : 61 760 /
516 000 =0,1197 ~0,12.
c. Calculer la
probabilité conditionnelle de l’évènement B sachant que l’évènement A
est réalisé, notée PA(B).
PA(B)=P(A∩B) / P(A) = 0,1197 / 0,8721 = 0,137 ~0,14 ( ou 61 760 / 450 000 ) ~0,14
).
Nlle Calédonie.
Une association s’adresse à une agence de voyage pour organiser un
séjour de vacances pour ses 210 adhérents.
On constate que, parmi ces adhérents :
30% ont moins de 40 ans ; un tiers souhaite séjourner en Amérique ;
40% souhaitent séjourner en Europe, et parmi eux, 75% ont plus de 40
ans ;
47 adhérents âgés de plus de 40 ans souhaitent séjourner en Afrique.
1. Recopier et
compléter le tableau suivant :
|
Nombre
d'adhérents désirant
séjourner en Europe |
Nombre
d'adhérents désirant
séjourner en Afrique |
Nombre
d'adhérents désirant
séjourner en Amérique
|
Total
|
Nombre
d'adhérents ayant plus de 40 ans
|
84
x0,75 =63
|
47
|
147-47-63
= 37
|
210-63=147
|
| Nombre
d'adhérents ayant moins de 40 ans |
21
|
56-47=9
|
70-37=33
|
210
x0,30 = 63 |
Total
|
210
x0,4 =84
|
210-84-70=56
|
210
/3 = 70
|
210 |
Dans les questions suivantes,
on donnera les résultats sous forme décimale, arrondis au centième.
On choisit au hasard un adhérent de l’association. On suppose que tous
les adhérents ont lamême probabilité d’être choisis.
2. Calculer la
probabilité de chacun des évènements suivants :
A : « l’adhérent souhaite séjourner en Afrique » ; P(A) = 56 / 210 =
0,2667 ~0,27.
B : « l’adhérent est âgé de plus de 40 ans ».P(B) = 147 / 210 =0,70.
3. Calculer la
probabilité de chacun des évènements A∩B et A∪B.
P(A∩B) =47 / 210
=0,2238 ~0,22. P(A∪B) =P(A)
+P(B) -P(A∩B) =0,2667
+0,70 -0,2238 =0,7429 ~0,74.
4.
Calculer la probabilité que l’adhérent souhaite se rendre en Afrique
sachant qu’il est âgé de plus de 40 ans.
PB(A) = 47 / 147 =0,32.
|
|