Mathématiques,
probabilités
Bac St2S 2016.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
Métropole 2016.
L’embolie pulmonaire correspond à l’obstruction d’une artère pulmonaire
par un caillot circulant dans le sang. Un test sanguin fondé sur le
dosage de certaines molécules, les D-dimères, permet d’éclairer le
diagnostic lorsqu’une embolie pulmonaire est suspectée. Pour étudier
l’efficacité de ce test sanguin, on a réalisé une étude sur un groupe
de 1 000 patients dont il ressort que :
• 364 patients ont un test sanguin négatif et, parmi eux, 4 sont
néanmoins atteints d’une embolie
pulmonaire.
• 800 patients ne sont pas atteints d’une embolie pulmonaire.
1. Compléter le
tableau suivant.
|
Patient
atteint d'une embolie pulmonaire
|
Patient
non atteint d'une embolie pulmonaire |
Total
|
Test
positif
|
196
|
440
|
636
|
Test
négatif
|
4
|
360
|
364
|
Total
|
200
|
800
|
1000
|
2. On choisit le dossie médical d’un
patient au hasard parmi les 1 000 patients ayant été testés.
Chaque dossier a lamême probabilité d’être choisi. On considère les
évènements suivants :
T : « Le test sanguin du patient est positif » et T son évènement
contraire ;
M : « Le patient est atteint d’une embolie pulmonaire » et M son évènement
contraire.
a. Quelle est la
probabilité que le test sanguin du patient soit positif ?
Nombre total de test positif / nombre total de patient =636 / 1000 = 0,636.
b. Calculer P(M) et
PM(T ).
P(M) = 200 / 1000 = 0,20.
PM(T ) = 196 / 200 = 0,98.
c. Exprimer par une phrase
l’évènement M ∩T puis montrer que sa probabilité est 0,196.
Les patients sont atteints d'une embolie pulmonaire et leurs tests
sanguins sont positifs.
p(M ∩T) = 196 / 1000 = 0,196.
3. On donne les
définitions suivantes
Valeur prédictive
positive : probabilité d’avoir une embolie pulmonaire sachant
que le test
sanguin est positif.
Valeur prédictive
négative : probabilité de ne pas avoir une embolie pulmonaire
sachant que le test
sanguin est négatif.
a.
Calculer PT (M). On donnera une valeur approchée, arrondie
au millième.
Interpréter le résultat
obtenu en termes de valeur prédictive.
PT (M) =196 / 636 = 0,308.
Parmi 1000 patients ayant un test positif, 308 sont atteints d'embolie
pulmonaire.
b. Montrer que la valeur prédictive
négative de ce test sanguin est environ 0,989.
360 / 364 =0,989.
c. En examinant les deux résultats
précédents, conclure quant à l’utilité de ce test sanguin pour
le diagnostic de
l’embolie pulmonaire.
Ce test n'est pas utile : 30,8 % des patients ont un test positif alors
qu'ils ne sont pas atteints d'embolie pulmonaire et 1,1 % des patients
atteints on un test négatif.
|
|
|
Métropole septembre 2016.
La
contraception d’urgence est une méthode contraceptive d’exception
destinée à réduire les possibilités de grossesses non désirées.
Partie A.
Le tableau ci-dessous donne l’évolution des ventes de boîtes de
contraception d’urgence.
Année
|
2003
|
2005
|
2007
|
2009
|
2011
|
Rang
de l'année : xi
|
1
|
2
|
3
|
4
|
5
|
Nombre
de boîtes ( millions) : yi
|
0,81
|
1,04
|
1,18
|
1,26
|
1,28
|
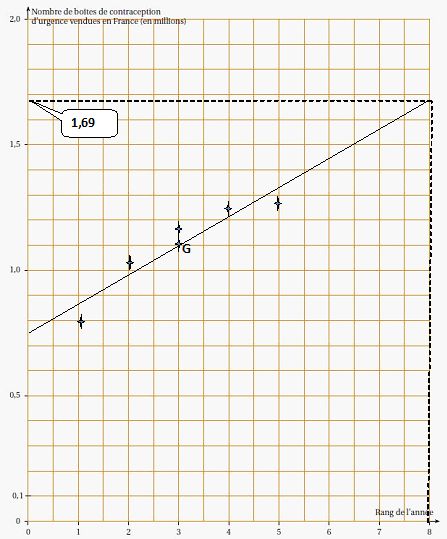
1.
Sur le graphique, représenter le nuage de points de coordonnées (xi
: yi ).
2. Calculer les
coordonnées du point moyen G du nuage. Placer le point G sur le
graphique.
xmoyen = (1 +2 +3 +4 +5 ) /5 = 3.
ymoyen = (0,81 +1,04 +1,18 +1,26 +1,28) / 5 = 1,114.
3. On admet que la
droite (d) d’équation y = 0,116x+0,766 constitue un bon ajustement de
la série étudiée.
a. Justifier par un
calcul que le point G appartient à la droite (d).
b. Construire la
droite (d) dans le repère.
y(3) = 0,116 *3 +0,766= 1,114. On trouve l'ordonnée de G. G appartient
à cette droite.
4. On admet que
l’ajustement réalisé par la droite (d) reste valable jusqu’en 2017.
Estimer, par la méthode de votre choix, le nombre de boîtes de
contraception d’urgence vendues en France en 2017.
xi = 8, lecture graphe : yi = 1,69 millions.
Par le calcul : y = 0,116 *8 +0,766 = 1,694 millions.
Partie B.
Un laboratoire pharmaceutique
français commercialise sous sa marque des boîtes de contraception
d’urgence. Il organise chaque année
un sondage pour déterminer la part de la population française
connaissant sa marque. Les
résultats obtenus ont été placés dans une feuille de calcul automatisée.
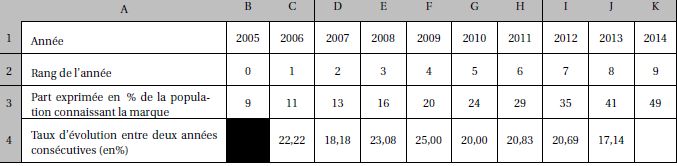
1. Les cellules de la ligne 4, de C4
à K4, sont au format pourcentage.
a. Donner une formule qui, saisie
dans la cellule C4 et recopiée vers la droite, permet de compléter la ligne 4.
=(C$3 - B$3) / B$3.
b. Calculer la valeur qui devrait
alors s’afficher dans la cellule K4.
(49-41) / 41 *100 = 19,51 %.
2. Les responsables du laboratoire
pharmaceutique observent que la part de la population française qui connaît sa marque progresse d’environ 20%
par an. Ils décident de modéliser cette évolution par une suite géométrique (un).
On note un une
estimation de la part (exprimée en %) de la population française qui
connaît la marque du
contraceptif d’urgence à l’année (2005+n). Ainsi le premier terme de la suite (un)
est donné par u0 = 9.
a. Donner la raison de la suite
géométrique (un) puis exprimer un en fonction de
n.
u1 = (1+0,20) u0 = 1,20 u0 ; u2 = 1,20 u1 = 1,202 u0 ; un = 1,20nu0 ; raison de la suite 1,20.
b. Calculer u10 puis
donner une interprétation du résultat dans le contexte de l’exercice.
u10 = 9 x 1,2010 =55,73
%.
En 2015, 55,73 % de la population connaît la marque cette boîte.
c. Résoudre l’inéquation 9×1,2x
>=75.
1,2 x >=75 / 9 ; x log 1,2 >= log ( 75 / 9) ; 0,07918
x >=0,9208 ; x >= 11,6.
d. Interpréter les solutions de la
question précédente dans le contexte de l’exercice.
Fin 2017, 75 % de la population française connaît la marque de cette
boîte.
|
|
|
|
Antilles Guyane 2016.
Les
trois principaux services de soins d’un centre hospitalier sont : le
service hématologie, le service diabétologie, le service urologie.
On s’intéresse aux prises de sang effectuées dans cet hôpital.
Après observation sur une assez longue période, on a constaté que :
• 50% des prises de sang sont effectuées dans le service hématologie ;
• 20% des prises de sang sont effectuées dans le service diabétologie ;
• Les autres le sont dans le service urologie.
Les seringues utilisées pour effectuer les prises de sang sont fournies
soit par le laboratoire Clamex, soit par le laboratoire Spara :
• dans le service hématologie, 56% des prises de sang sont effectuées
avec des seringues fournies par le laboratoire Clamex ;
• dans le service diabétologie, 80% des prises de sang sont effectuées
avec des seringues fournies par le laboratoire Spara ;
• dans le service urologie, la moitié des prises de sang sont
effectuées avec des seringues fournies par le laboratoire Clamex.
On choisit au hasard et de manière équiprobable un patient qui a subi
une prise de sang dans l’un des trois services citées précédemment.
On considère les évènements suivants :
H : « La prise de sang a été effectuée dans le service hématologie » ;
D : « La prise de sang a été effectuée dans le service diabétologie » ;
U : « La prise de sang a été effectuée dans le service urologie » ;
C : « La seringue utilisée pour ce patient a été fournie par le
laboratoire Clamex » ;
S : « La seringue utilisée pour ce patient a été fournie par le
laboratoire Spara ».
1. Compléter
l’arbre des probabilités.
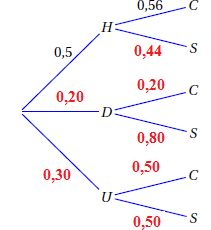
2. Dans cette
question, on s’intéresse à la seringue utilisée pour le patient choisi.
a. Déterminer la
probabilité de l’évènement « le patient choisi a subi une prise de sang
dans le service diabétologie avec une seringue fournie par le
laboratoire Spara ».
p(S ∩D) =0,20 x 0,8 = 0,16.
b. Calculer la
probabilité de l’évènement S.
p(S)=0,5 x 0,44 + 0,20 x 0,80 +0,30 x 0,50 =0,22 +0,16 +0,15 = 0,53.
c. Calculer la
probabilité que la seringue utilisée provienne du service diabétologie
sachant qu’elle a été fournie par le laboratoire Spara.
pS(D) =p(S ∩D) / P(S) =0,16 / 0,53 = 0,302.
d. Un personnel
soignant affirme : « Il est plus probable que la seringue utilisée
provienne du laboratoire Clamex que du laboratoire Spara. »
Cette affirmation est-elle correcte ? Justifier la réponse.
Cette affirmation est fausse. 53 % des seringues proviennent du
laboratoire Spara.
|
|
Polynésie 2016.
La caisse nationale de l’assurance maladie des travailleurs salariés
(CNAMTS) a étudié une population de personnes ayant eu recours à un
soin médical suite à un accident de la vie courante.
Selon cette enquête :
- 61% de ces accidents de la vie courante sont domestiques
(survenus dans la maison ou son environnement immédiat) ;
- parmi les accidents domestiques, 9% nécessitent de la rééducation ;
- parmi les accidents de la vie courante qui ne sont pas
domestiques, 18% nécessitent de la rééducation.
On interroge au hasard une personne dans la population étudiée et on
considère les évènements suivants.
D : « la personne a eu un accident domestique » ;
R : « la personne a eu un accident nécessitant de la rééducation ».
On note D
l’évènement contraire de D et R l’évènement contraire
de R.
1. Déterminer la
probabilité de l’évènement D, notée p(D).
p(D) = 0,61.
2. Donner la
probabilité pD(R),
probabilité de l’évènement R sachant D.
Probabilité de
rééducation lors d'un accident non domestique 18 %.
3.
Compléter l’arbre pondéré de probabilités fourni qui décrit la
situation.
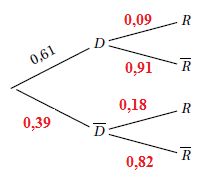
4. a. Montrer que
la probabilité que la personne ait eu un accident domestique
nécessitant de la rééducation est environ égale à 0,055, valeur
arrondie au millième.
0,61 x 0,09 = 0,055.
b. Décrire par une
phrase l’évènement D
∩R et calculer la probabilité de cet évènement. On arrondira le
résultat aumillième.
0,39 x 0,18 = 0,0705 ~0,071 ( 7,1 %).
7,1 % des personnes ayant eu un accident non domestique nécessite de la
rééducation.
c. Suite à cette
enquête, la CNAMTS estime que 12,5% des accidents de la vie courante
nécessitent de la rééducation. Justifier ce résultat.
0,09 x 0,61 + 0,18 x 0,39 = 0,0549 + 0,0702 = 0,125 ( 12,5 %).
5. Calculer
la probabilité de l’évènement contraire à D sachant R. On
arrondira le résultat au centième. Interpréter ce résultat.
0,39
*0,18 / 0,125 = 0,56 ( ~56 %).
56 % des personnes ayant eu un accident non domestique nécessite de la
rééducation.
Nlle Calédonie.
Une enquête a été menée en Europe en 2011 sur les conditions de travail
en entreprise.
Les résultats concernent les français sont les suivants :
- 61% des personnes interrogées considèrent que leur charge de travail
est importante ;
- 75% des personnes interrogées sont motivées par leur travail ;
- 43% des personnes interrogées sont motivées et considèrent que leur
charge de travail est importante.
1. On a commencé à
remplir un tableau qui résume les résultats de l’enquête pour un
échantillon représentatif de 100 personnes.
Compléter ce tableau.
Nombre
de personnes qui
|
considèrent
que leur charge
de travail est importante
|
considèrent
que leur charge
de travail n'est pas importante |
Total
|
sont
motivées par leur travail
|
43
|
75-43=32
|
75
|
| ne
sont pas motivées par leur travail |
61-43=18
|
39-32=7
|
25
|
Total
|
61
|
100-61
=39
|
100
|
On choisit au hasard une personne interrogée dans cette enquête.
On considère les évènements suivants :
C : « La personne interrogée pense que sa charge de travail est
importante » ;
M : « La personne interrogée est motivée par son travail ».
Dans toute la suite, on arrondira si nécessaire, les résultats
aumillième.
2. Donner les
probabilités des évènements : C et celle de l'événement " la charge de
travail est importante et.n'est pas motivée"
P(C) =0,61 ; P(la charge de
travail est importante et.n'est pas motivée)=0,18.
3. Calculer la
probabilité 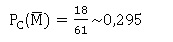
4. Montrer que la probabilité de l’évènement suivant est égale à 0,82.
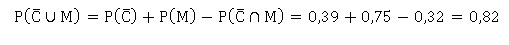
5. L’enquête a été
réalisée dans d’autres pays que la France. Ainsi, on a interrogé 9 145
européens dont 1 012 étaient français.
On choisit une personne au hasard parmi ces 9 145 européens.
a. Quelle est la
probabilité qu’elle soit française ? P(F)=1012 / 9145=0,111.
b. Quelle est la
probabilité qu’elle soit française et qu’elle soit motivée par son
travail ?
P(F n M)=0,111 x 0,75=0,083.
|
|