Etudes de fonctions, bac Sti2d. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Soit f la fonction définie sur ]0 ; +oo[ par : f (x) =1/x-ln x. On appelle Cf sa courbe représentative dans un repère orthonormal. Sur le graphique ci-dessous, on donne Cf et les courbes C et G. L’une de ces deux courbes représente graphiquement la dérivée f ′ de f , et l’autre une des primitives F de f . Indiquer laquelle des deux courbes C et G représente graphiquement f ′. Justifier. 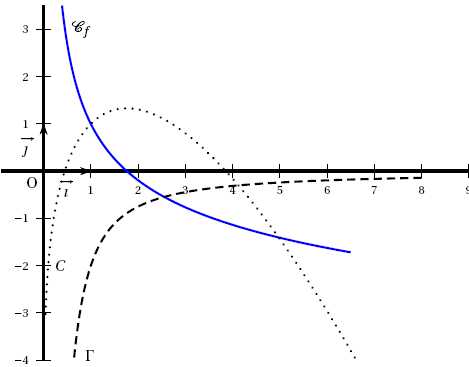La fonction f(x) est décroissante, sa dérivée est donc négative ( courbe G). Par lecture graphique, donner F(1). Courbe C : F(1) = 1. Dans cette question, on pourra vérifier la cohérence des résultats obtenus avec les courbes représentatives données sur le dessin.  Déterminer la limite de la fonction f quand x tend vers 0. Interpréter graphiquement cette limite.  1/x tend vers +oo quand x tend vers zéro par valeur positive ; -ln x tend vers +oo quand x tend vers zéro : f(x) tend vers l'infini quand x tend vers zéro : la droite x=0 est asymptote. Déterminer la limite de la fonction f quand x tend vers +oo.  1/x tend vers zéroo quand x tend vers l'infini ; -ln x tend vers -oo quand x tend vers l'infini : f(x) tend vers -oo quand x tend vers l'infini. Calculer f ′(x) et montrer que l’on peut écrire : f ′(x) =(-x-1)/x2. Dérivée de 1/x : -1/x2 ; dérivée de -lnx : -1/x ; dérivée de f(x) : f '(x) =-1/x2-1/x =(-x-1)/x2. 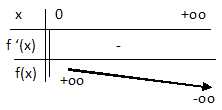Étudier le signe de f ′(x) puis donner le tableau de variations de f. Sur l'intervalle ]0 ; +oo[, la dérivée est négative. Soit H la fonction définie sur ]0 ; +∞[ par : H(x) = x −(x −1) lnx. Montrer que H est une primitive de f sur ]0 ; +∞[. Dériver H ; on pose u =x-1 et v = ln x ; u' = 1 et v' = 1/x. H'(x) =1-(u'v+v'u) = 1-(lnx+(x-1)/x)=1-lnx-1+1/x = 1/x -lnx = f(x). En déduire l’expression de la fonction F. F = H +cste avec F(1) =1 ; H(1) +Cste =1 ; 1-(1-1)ln1 +Cste =1 soit Cste = 1. F(x) =x-(x-1)lnx. Calculer I= 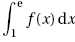. I = [=x-(x-1)lnx]1e=e-(e-1)ln e -(1-(1-1)ln1) =0. Un architecte veut établir les plans d’un hangar pour ballon dirigeable. La forme de la façade avant de ce hangar et les points O, A, B, S, H et K sont donnés sur le schéma ci-dessous. . . . . Cette façade avant est symétrique par rapport au segment vertical [OS] et OH= 30 m. L’arc SA de la façade avant correspond à une partie de la représentation graphique d’une fonction définie sur l’intervalle [0 ; 60], dans un repère orthonormal direct d’origine O du plan, l’unité étant le mètre. Le cahier des charges impose les quatre conditions suivantes : OS = 60 ; HK > 35 ; la fonction évoquée ci-dessus doit être strictement décroissante sur l’intervalle [0 ; 60] ;  OA <=0. Vérifier que la fonction f définie sur l’intervalle [0 ; 60] par f (x) = 80−20e0,025x vérifie les trois premières conditions du cahier des charges. OS =f(0) =80-20e0=80-20 = 60. HK = f(30) =80-20e0,025*30=80-42,3 = 37,7, valeur supérieure à 35 m. f '(x) =-20*0,025e0,025x  est strictement négative sur [0; 60 ] ; f(x) est décroissante sur cet intervalle. Déterminer, à l’aide de la calculatrice, la valeur décimale approchée à 10−1 près par excès du réel a qui vérifie f (a)= 0. 0 = 80-20 e0,025a ; 4 =e0,025a  ; ln 4 = 0,025 a ; a =55,452 ~55,5. Vérifier que la quatrième condition du cahier des charges est remplie. OA = a = 55,5, valeur inférieure à 60 m. La fonction F est définie sur l’intervalle [0 ; 60] par F(x)= 80x −800e0,025x . Vérifier que la fonction F est une primitive de la fonction f sur l’intervalle [0 ; 60]. F'(x) =80 -800*0,025e0,025x =80-20e0,025x =f(x). Calculer la valeur exacte de l’intégrale I. 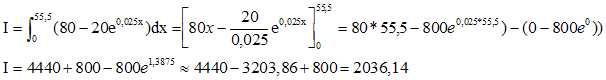On souhaite peindre la surface extérieure de la façade avant. Déterminer à 10−2 près l’aire de cette surface exprimée en m2. A =2 I =2*2036,14=4072,28 m2. La peinture utilisée pour peindre la surface extérieure de la façade avant est vendue en bidons de 68 litres. Sachant que cette peinture a une propriété de recouvrement de 0,2 mètre carré par litre, combien de bidons sont nécessaires pour peindre la surface extérieure de la façade avant ? Surface peinte : 0,2*68 =13,6 m2 par bidon. 4072,28/ 13,6 =299,4 ~300 bidons. . .

menu